九年级数学苏科版上册 2.2 圆的对称性 课时练(word版 含答案)
文档属性
| 名称 | 九年级数学苏科版上册 2.2 圆的对称性 课时练(word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 248.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 11:22:11 | ||
图片预览

文档简介
课 时 练
2.2 圆的对称性
一、选择题(本大题共10小题,共30分)
下列说法中,正确的是( )
A. 相等的弦所对的弧相等
B. 在同圆或等圆中,相等的弧所对的圆心角相等
C. 在同圆或等圆中,较长的弧所对的弦较长
D. 相等的圆心角所对的弧相等
下列说法正确的是( )
A. 直径是弦,弦是直径
B. 圆有无数条对称轴
C. 无论过圆内哪一点,都只能作一条直径
D. 度数相等的弧是等弧
在O中,弦AB等于圆的半径,则该弦所对的弧的度数为( )
A. B. C. D. 以上都不对
如图,在O中,若C是的中点,A=,则BOC的度数为( )
A. B.
C. D.
圆是轴对称图形,它的对称轴有( )
A. 条 B. 条 C. 条 D. 无数条
如图,O的直径ABCD于点E,则下列结论不一定正确的是( )
A. B.
C. D.
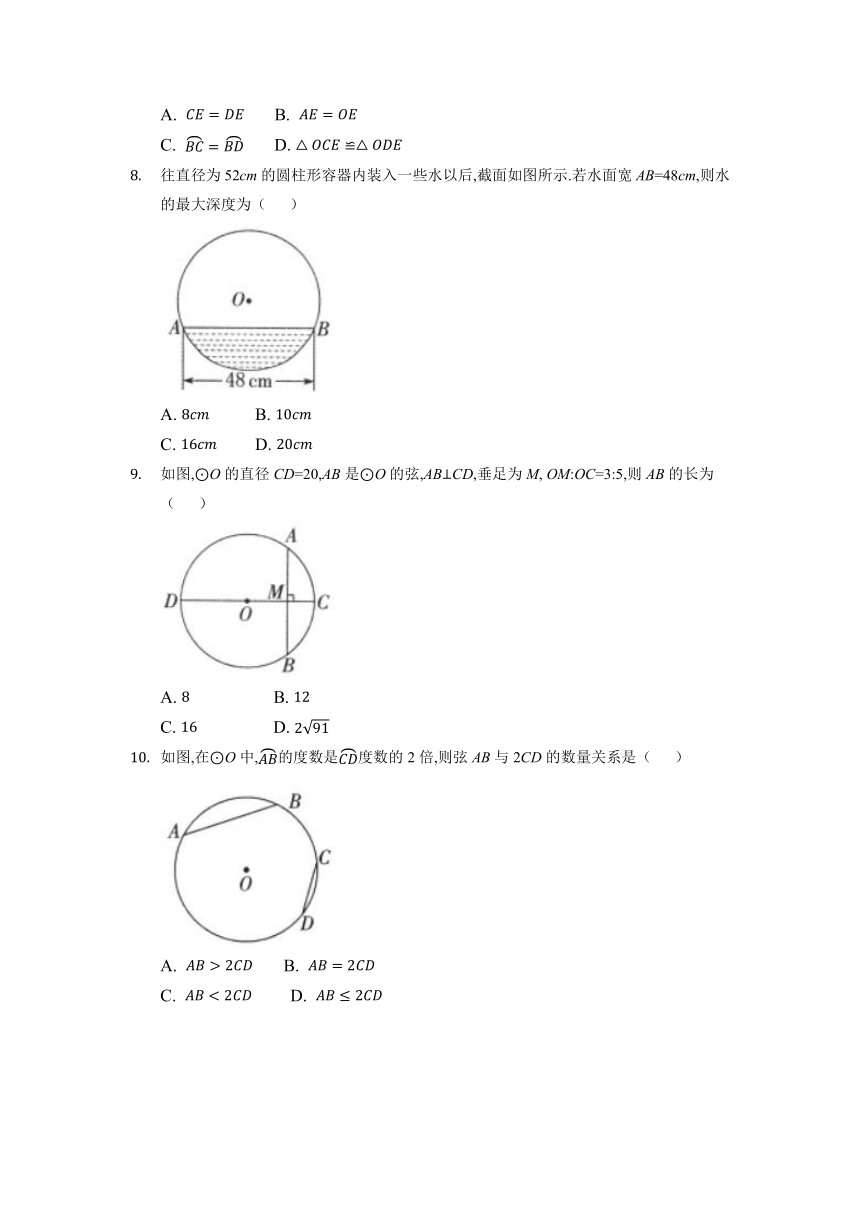
往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示.若水面宽AB=48cm,则水的最大深度为( )
A. B.
C. D.
如图,O的直径CD=20,AB是O的弦,ABCD,垂足为M, OM:OC=3:5,则AB的长为( )
A. B.
C. D.
如图,在O中,的度数是度数的2倍,则弦AB与2CD的数量关系是( )
A. B.
C. D.
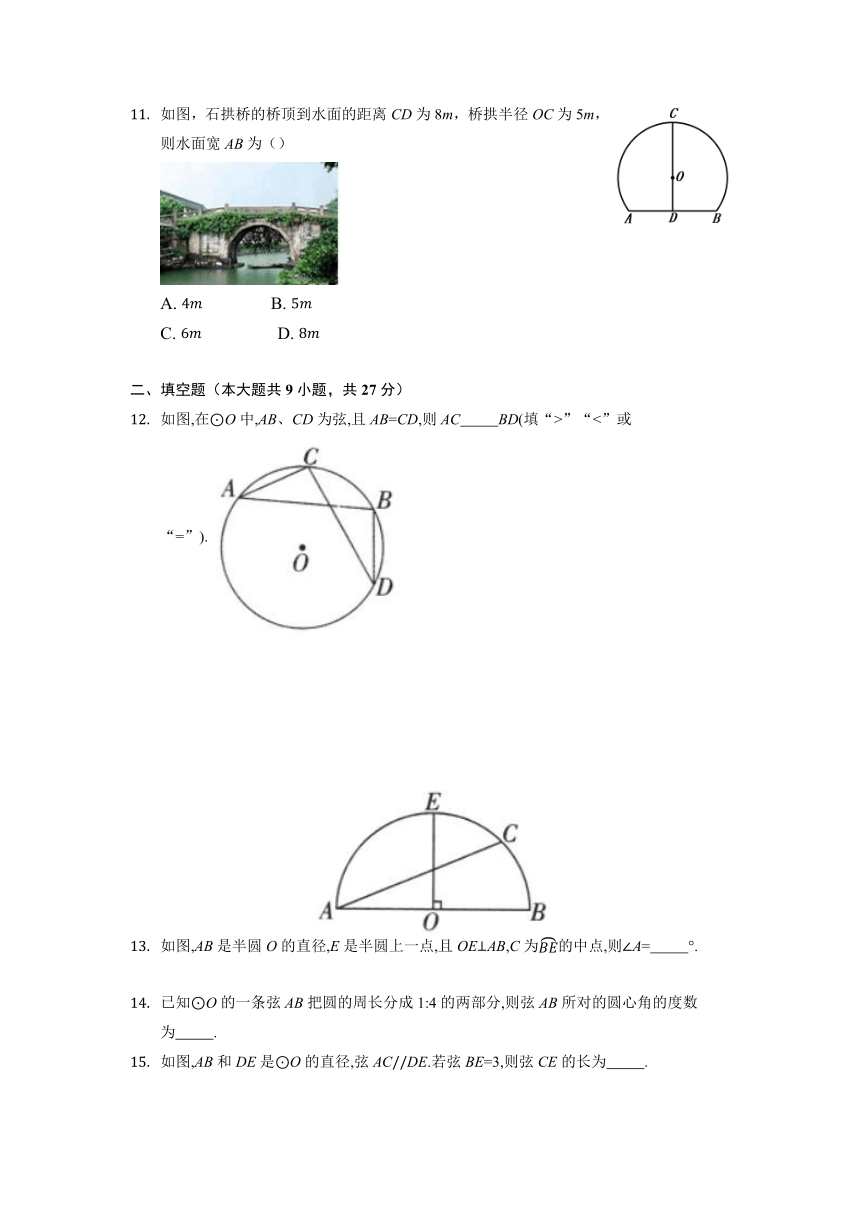
如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为()
A. B.
C. D.
二、填空题(本大题共9小题,共27分)
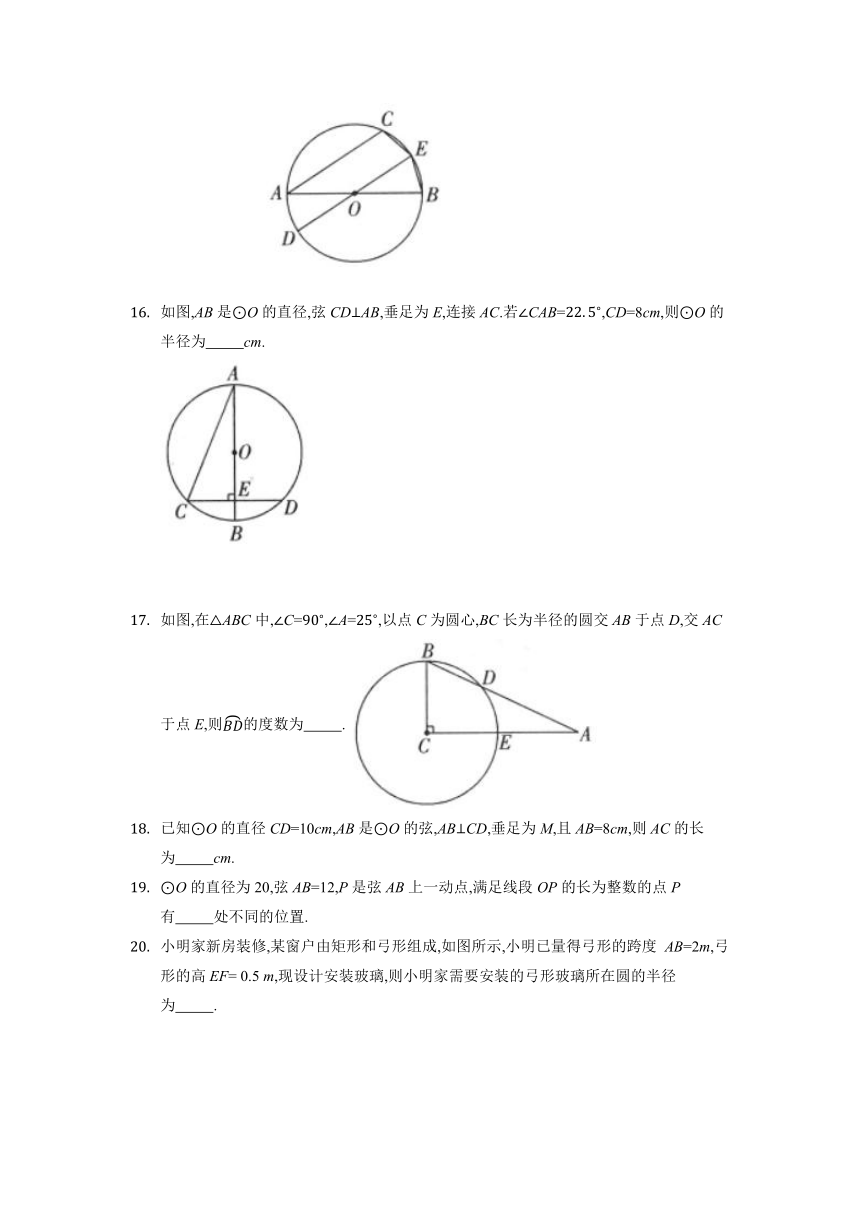
如图,在O中,AB、CD为弦,且AB=CD,则AC BD(填“>”“<”或“=”).
如图,AB是半圆O的直径,E是半圆上一点,且OEAB,C为的中点,则A= °.
已知O的一条弦AB把圆的周长分成1:4的两部分,则弦AB所对的圆心角的度数为 .
如图,AB和DE是O的直径,弦ACDE.若弦BE=3,则弦CE的长为 .
如图,AB是O的直径,弦CDAB,垂足为E,连接AC.若CAB=,CD=8cm,则O的半径为 cm.
如图,在ABC中,C=,A=,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则的度数为 .
已知O的直径CD=10cm,AB是O的弦,ABCD,垂足为M,且AB=8cm,则AC的长为 cm.
O的直径为20,弦AB=12,P是弦AB上一动点,满足线段OP的长为整数的点P有 处不同的位置.
小明家新房装修,某窗户由矩形和弓形组成,如图所示,小明已量得弓形的跨度 AB=2m,弓形的高EF= 0.5 m,现设计安装玻璃,则小明家需要安装的弓形玻璃所在圆的半径为 .
三、解答题(本大题共4小题,共43分)
如图,正方形ABCD的四个顶点都在O上,M为的中点,连接BM、CM.
求证:BM=CM.
如图,在O中,C是的中点,CDOA于点D,CEOB于点E.
求证:AD=BE.
如图,在O中,=2,ADOC于点D.
求证:AB=2AD.
如图,在RtABC中,C=,以点C为圆心,AC长为半径的C与AB相交于点D.已知AC=6,BC=8,求AD的长.
参考答案
1.B
2. B
3. D
4. A
5. D
6. B
7. C
8. C
9. C
10. D
11. =
12. 22.5
13.
14. 3
15. 4
16.
17. 2或4
18. 5
19. 1.25m
20.证明:四边形ABCD是正方形,AB=CD.=.
M为的中点,=.
+=+,即=.
BM=CM.
21.解:如图,连接OC.
C是的中点,=.
AOC=BOC.
CDOA,CEOB,CDO=CEO=.
在COD和COE中,
CODCOE.OD=OE.
OA=OB,AD=BE
22. 证明:如图,延长AD交O于点E.
OC过圆心O,OCAD,
=2,AE=2AD.
=2,=.
AB=AE.AB=2AD
23.解:如图,连接CD,过点C作CHAB于点H,则AH=AD.
在RtABC中,由勾股定理,得AB===10.
由=ACBC=ABCH,即68=10CH,得CH=.
在RtAHC中,由勾股定理,得AH===.
AD=2AH=.
2.2 圆的对称性
一、选择题(本大题共10小题,共30分)
下列说法中,正确的是( )
A. 相等的弦所对的弧相等
B. 在同圆或等圆中,相等的弧所对的圆心角相等
C. 在同圆或等圆中,较长的弧所对的弦较长
D. 相等的圆心角所对的弧相等
下列说法正确的是( )
A. 直径是弦,弦是直径
B. 圆有无数条对称轴
C. 无论过圆内哪一点,都只能作一条直径
D. 度数相等的弧是等弧
在O中,弦AB等于圆的半径,则该弦所对的弧的度数为( )
A. B. C. D. 以上都不对
如图,在O中,若C是的中点,A=,则BOC的度数为( )
A. B.
C. D.
圆是轴对称图形,它的对称轴有( )
A. 条 B. 条 C. 条 D. 无数条
如图,O的直径ABCD于点E,则下列结论不一定正确的是( )
A. B.
C. D.
往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示.若水面宽AB=48cm,则水的最大深度为( )
A. B.
C. D.
如图,O的直径CD=20,AB是O的弦,ABCD,垂足为M, OM:OC=3:5,则AB的长为( )
A. B.
C. D.
如图,在O中,的度数是度数的2倍,则弦AB与2CD的数量关系是( )
A. B.
C. D.
如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为()
A. B.
C. D.
二、填空题(本大题共9小题,共27分)
如图,在O中,AB、CD为弦,且AB=CD,则AC BD(填“>”“<”或“=”).
如图,AB是半圆O的直径,E是半圆上一点,且OEAB,C为的中点,则A= °.
已知O的一条弦AB把圆的周长分成1:4的两部分,则弦AB所对的圆心角的度数为 .
如图,AB和DE是O的直径,弦ACDE.若弦BE=3,则弦CE的长为 .
如图,AB是O的直径,弦CDAB,垂足为E,连接AC.若CAB=,CD=8cm,则O的半径为 cm.
如图,在ABC中,C=,A=,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则的度数为 .
已知O的直径CD=10cm,AB是O的弦,ABCD,垂足为M,且AB=8cm,则AC的长为 cm.
O的直径为20,弦AB=12,P是弦AB上一动点,满足线段OP的长为整数的点P有 处不同的位置.
小明家新房装修,某窗户由矩形和弓形组成,如图所示,小明已量得弓形的跨度 AB=2m,弓形的高EF= 0.5 m,现设计安装玻璃,则小明家需要安装的弓形玻璃所在圆的半径为 .
三、解答题(本大题共4小题,共43分)
如图,正方形ABCD的四个顶点都在O上,M为的中点,连接BM、CM.
求证:BM=CM.
如图,在O中,C是的中点,CDOA于点D,CEOB于点E.
求证:AD=BE.
如图,在O中,=2,ADOC于点D.
求证:AB=2AD.
如图,在RtABC中,C=,以点C为圆心,AC长为半径的C与AB相交于点D.已知AC=6,BC=8,求AD的长.
参考答案
1.B
2. B
3. D
4. A
5. D
6. B
7. C
8. C
9. C
10. D
11. =
12. 22.5
13.
14. 3
15. 4
16.
17. 2或4
18. 5
19. 1.25m
20.证明:四边形ABCD是正方形,AB=CD.=.
M为的中点,=.
+=+,即=.
BM=CM.
21.解:如图,连接OC.
C是的中点,=.
AOC=BOC.
CDOA,CEOB,CDO=CEO=.
在COD和COE中,
CODCOE.OD=OE.
OA=OB,AD=BE
22. 证明:如图,延长AD交O于点E.
OC过圆心O,OCAD,
=2,AE=2AD.
=2,=.
AB=AE.AB=2AD
23.解:如图,连接CD,过点C作CHAB于点H,则AH=AD.
在RtABC中,由勾股定理,得AB===10.
由=ACBC=ABCH,即68=10CH,得CH=.
在RtAHC中,由勾股定理,得AH===.
AD=2AH=.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
