专题1.4 第一章 勾股定理(单元小结) 课件(共57张PPT)
文档属性
| 名称 | 专题1.4 第一章 勾股定理(单元小结) 课件(共57张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 08:24:23 | ||
图片预览







文档简介
(共57张PPT)
八上数学同步精优课件
北师大版八年级上册
第一章 勾股定理
1.4单元小结
精优教学课件
新课导入
讲授新课
当堂检测
课堂小结
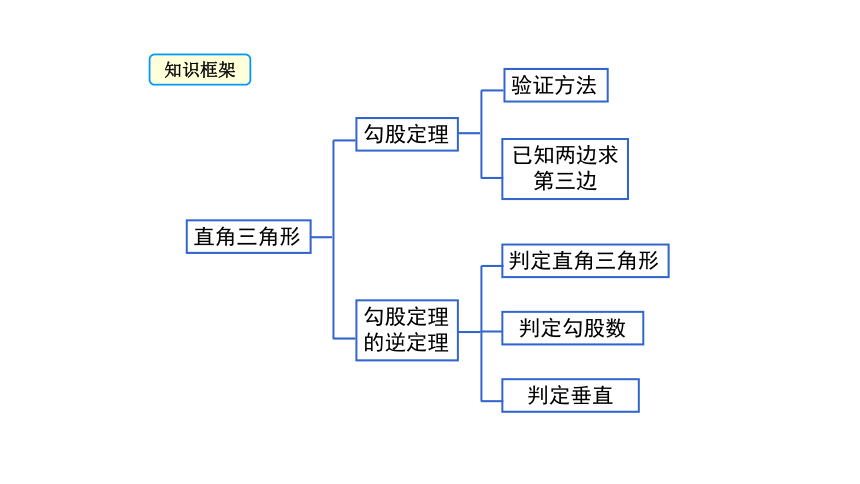
知识框架
勾股定理
勾股定理
的逆定理
直角三角形
验证方法
已知两边求
第三边
判定直角三角形
判定勾股数
判定垂直
知识汇总
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
已知Rt ABC的两直角边分别是3和4,则它的斜边是 .
5
勾股定理的应用条件
一、勾股定理
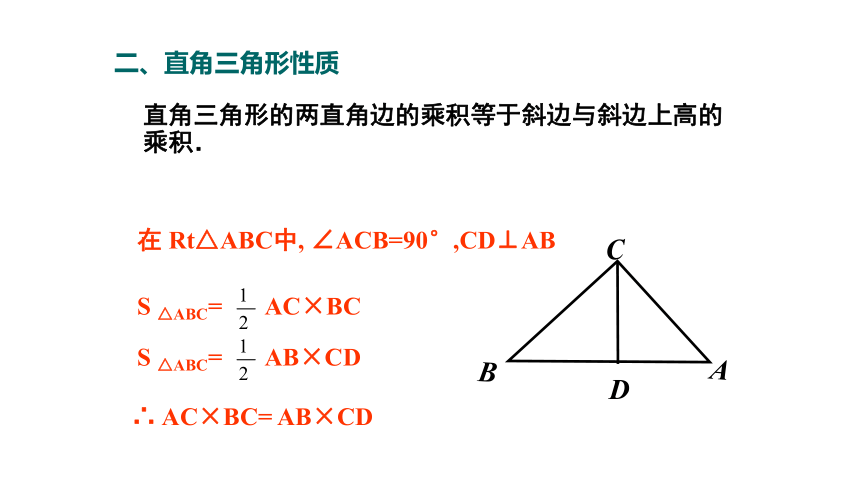
二、直角三角形性质
直角三角形的两直角边的乘积等于斜边与斜边上高的乘积.
A
D
B
C
在 Rt△ABC中, ∠ACB=90°,CD⊥AB
S △ABC= AC×BC
S △ABC= AB×CD
∴ AC×BC= AB×CD
勾股逆定理
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
勾股数
三、勾股逆定理与勾股数
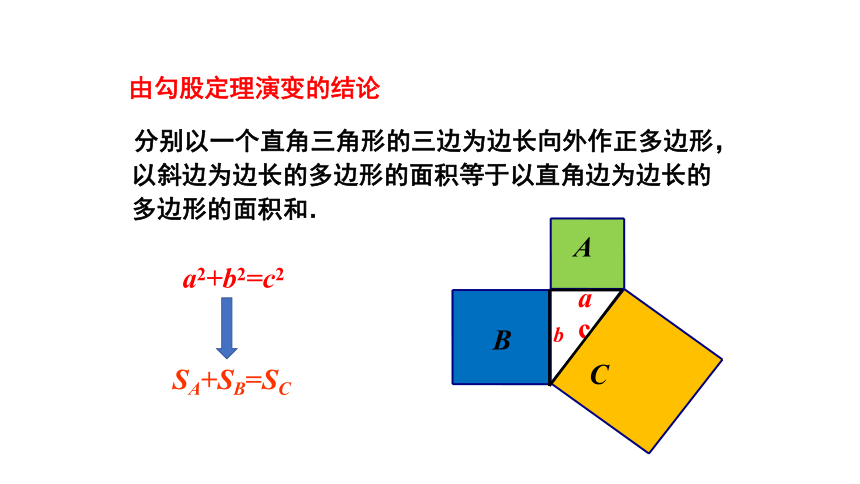
分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.
由勾股定理演变的结论
A
B
a
c
b
C
SA+SB=SC
a2+b2=c2
以“一个三角形是直角三角形”为条件,得出三角形三边有a2+b2=c2关系式成立.
一个三角形的三边a、b、c满足a2+b2=c2为条件,得出这个三角形是直角三角形的结论.
都与三角形三边有关
都与直角三角形有关
勾股定理
勾股逆定理
区
别
联
系
四、勾股定理与勾股逆定理的比较
(1)在不规则的几何图形中,通常添加辅助线得到直角三角形.
(2)常见的类型:
①勾股定理在几何中的应用:利用勾股定理求几何图形的面积和有关线段的长度.
②由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.
③勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.
五、勾股逆定理的应用
平面展开﹣最短路径问题
(1)根据题意把立体图形展开成平面图形
(2)再确定两点之间的最短路径.一般情况是两点之间,线段最短.
(3)在平面图形上构造直角三角形解决问题.
勾股定理的应用
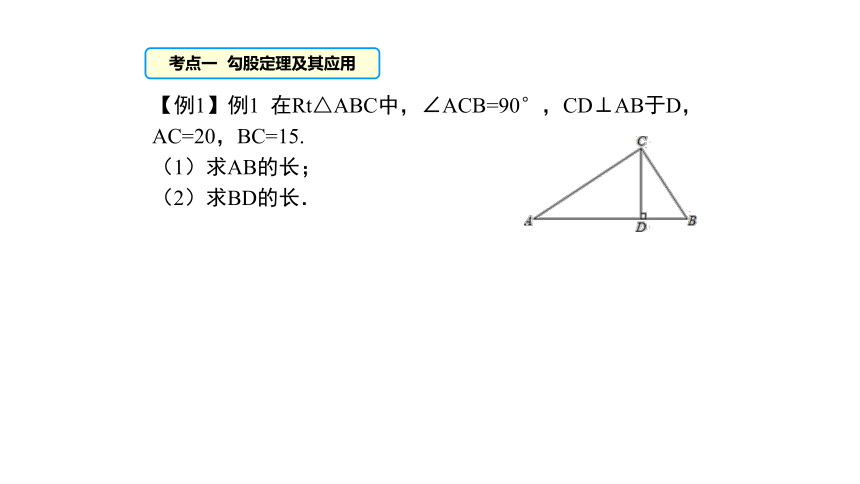
【例1】例1 在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15.
(1)求AB的长;
(2)求BD的长.
考点一 勾股定理及其应用
解:(1)∵在Rt△ABC中,∠ACB=90°,
(2)方法一:∵S△ABC= AC BC= AB CD,
∴20×15=25CD,
∴CD=12.
∴在Rt△BCD中,
方法二:设BD=x,则AD=25-x.
解得x=9.∴BD=9.
方法总结
对于本题类似的模型,若已知两直角边求斜边上的高常需结合面积的两种表示法起来考查,若是同本题(2)中两直角三角形共一边的情况,还可利用勾股定理列方程求解.
考点一 勾股定理及其应用2
例2 我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
解:如图,设水池的水深AC为x尺,
则这根芦苇长AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得BC2+AC2=AB2,
即 52+ x2= (x+1)2
25+ x2= x2+2x+1,
2x=24,
∴ x=12, x+1=13.
答:水池的水深12尺,这根芦苇长13尺.
D
B
C
A
考点三 勾股定理中最短路径问题
例3 如图所示,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处,问怎样走路线最短?最短路线长为多少?
解析:蚂蚁由A点沿长方体的表面爬行到C1点,有三种方式:
①沿ABB1A1和A1 B1C1D1面;②沿ABB1A1和BCC1B1面;③沿AA1D1D和A1B1C1D1面,把三种方式分别展成平面图形如下:
解: 在Rt△ABC1中,
在Rt△ACC1中,
在Rt△AB1C1中,
∴沿路径 走路径最短,最短路径长为5.
化折为直:长方体中求两点之间的最短距离,展开方法有多种,一般沿最长棱展开,距离最短.
方法总结
【例4】在O处的某海防哨所发现在它的北偏东60°方向相距1000米的A处有一艘快艇正在向正南方向航行,经过若干小时后快艇到达哨所东南方向的B处.
(1)此时快艇航行了多少米(即AB 的长)?
(2)距离哨所多少米(即OB的长) ?
考点四 勾股定理实际应用
北
东
O
A
B
60°
45°
C
解:根据题意得∠AOC=30°,
∠COB=45°,AO=1000米.
∴AC=500米,BC=OC.
在Rt△AOC中,由勾股定理得
∴BC=OC=
北
东
O
A
B
60°
45°
C
解:在Rt△BOC中,由勾股定理得
针对训练
1.如图,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道,现有一辆卡车装满家具后,高4米,宽2.8米,请问这辆送家具的卡车能否通过这个通道?
在Rt△ABO中,OA=2米,DC=OB=1.4米,
∴AB2=22-1.42=2.04.
∵4-2.6=1.4,1.42=1.96,
2.04>1.96,
答:卡车可以通过,但要小心.
解:如图,过半圆直径的中点O,作直径的垂线交下底边于点D,取点C,使CD=1.4米,过C作OD的平行线交半圆直径于B点,交半圆于A点.
考点五 勾股定理的逆定理及其应用
例5 在△ABC中,AB=c,BC=a,AC=b, ,2c-b=12,求△ABC的面积.
解:由题意可设a=3k,则b=4k,c=5k,
∵2c-b=12,
∴10k-4k=12,
∴k=2,
∴a=6,b=8,c=10,
∵62+82=102,
∴a2+b2=c2,
∴△ABC为直角三角形,
∴△ABC的面积为 ×6×8=24.
考点六 勾股定理与折叠问题
例6 如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,求△ABE的面积.
解:∵长方形折叠,使点B与点D重合,
∴ED=BE.
设AE=xcm,则ED=BE=(9-x)cm,
在Rt△ABE中,
AB2+AE2=BE2,
∴32+x2=(9-x)2,
解得x=4.
∴△ABE的面积为3×4× =6(cm2).
方法总结
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
考点七 勾股定理特殊做题方法
例7 在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16.
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.∴BC=BD+CD=25,
∴△ABC的周长为25+20+15=60.
方法总结
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
当高AD在△ABC外部时,如图②.
同理可得 BD=16,CD=9.
∴BC=BD-CD=7,
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
针对训练
2 有一圆柱体高为8cm,底面圆的半径为2cm,如图.在AA1上的点Q处有一只蜘蛛,QA1=3cm,在BB1上的点P处有一只苍蝇,PB=2cm.求蜘蛛爬行的最短路径长(π取3).
解:如图,沿AA1剪开,过Q作QM⊥BB1于M,连接QP.
则PM=8-3-2=3(cm),
QM=A1B1= ×2×π×2=6(cm),
在Rt△QMP中,由勾股定理得
答:蜘蛛爬行的最短路径长是 cm.
当堂练习
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精优课件
北师大版八年级上册
第一章 勾股定理
1.4单元小结
精优教学课件
新课导入
讲授新课
当堂检测
课堂小结
知识框架
勾股定理
勾股定理
的逆定理
直角三角形
验证方法
已知两边求
第三边
判定直角三角形
判定勾股数
判定垂直
知识汇总
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
已知Rt ABC的两直角边分别是3和4,则它的斜边是 .
5
勾股定理的应用条件
一、勾股定理
二、直角三角形性质
直角三角形的两直角边的乘积等于斜边与斜边上高的乘积.
A
D
B
C
在 Rt△ABC中, ∠ACB=90°,CD⊥AB
S △ABC= AC×BC
S △ABC= AB×CD
∴ AC×BC= AB×CD
勾股逆定理
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
勾股数
三、勾股逆定理与勾股数
分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.
由勾股定理演变的结论
A
B
a
c
b
C
SA+SB=SC
a2+b2=c2
以“一个三角形是直角三角形”为条件,得出三角形三边有a2+b2=c2关系式成立.
一个三角形的三边a、b、c满足a2+b2=c2为条件,得出这个三角形是直角三角形的结论.
都与三角形三边有关
都与直角三角形有关
勾股定理
勾股逆定理
区
别
联
系
四、勾股定理与勾股逆定理的比较
(1)在不规则的几何图形中,通常添加辅助线得到直角三角形.
(2)常见的类型:
①勾股定理在几何中的应用:利用勾股定理求几何图形的面积和有关线段的长度.
②由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.
③勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.
五、勾股逆定理的应用
平面展开﹣最短路径问题
(1)根据题意把立体图形展开成平面图形
(2)再确定两点之间的最短路径.一般情况是两点之间,线段最短.
(3)在平面图形上构造直角三角形解决问题.
勾股定理的应用
【例1】例1 在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15.
(1)求AB的长;
(2)求BD的长.
考点一 勾股定理及其应用
解:(1)∵在Rt△ABC中,∠ACB=90°,
(2)方法一:∵S△ABC= AC BC= AB CD,
∴20×15=25CD,
∴CD=12.
∴在Rt△BCD中,
方法二:设BD=x,则AD=25-x.
解得x=9.∴BD=9.
方法总结
对于本题类似的模型,若已知两直角边求斜边上的高常需结合面积的两种表示法起来考查,若是同本题(2)中两直角三角形共一边的情况,还可利用勾股定理列方程求解.
考点一 勾股定理及其应用2
例2 我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
解:如图,设水池的水深AC为x尺,
则这根芦苇长AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得BC2+AC2=AB2,
即 52+ x2= (x+1)2
25+ x2= x2+2x+1,
2x=24,
∴ x=12, x+1=13.
答:水池的水深12尺,这根芦苇长13尺.
D
B
C
A
考点三 勾股定理中最短路径问题
例3 如图所示,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处,问怎样走路线最短?最短路线长为多少?
解析:蚂蚁由A点沿长方体的表面爬行到C1点,有三种方式:
①沿ABB1A1和A1 B1C1D1面;②沿ABB1A1和BCC1B1面;③沿AA1D1D和A1B1C1D1面,把三种方式分别展成平面图形如下:
解: 在Rt△ABC1中,
在Rt△ACC1中,
在Rt△AB1C1中,
∴沿路径 走路径最短,最短路径长为5.
化折为直:长方体中求两点之间的最短距离,展开方法有多种,一般沿最长棱展开,距离最短.
方法总结
【例4】在O处的某海防哨所发现在它的北偏东60°方向相距1000米的A处有一艘快艇正在向正南方向航行,经过若干小时后快艇到达哨所东南方向的B处.
(1)此时快艇航行了多少米(即AB 的长)?
(2)距离哨所多少米(即OB的长) ?
考点四 勾股定理实际应用
北
东
O
A
B
60°
45°
C
解:根据题意得∠AOC=30°,
∠COB=45°,AO=1000米.
∴AC=500米,BC=OC.
在Rt△AOC中,由勾股定理得
∴BC=OC=
北
东
O
A
B
60°
45°
C
解:在Rt△BOC中,由勾股定理得
针对训练
1.如图,某住宅社区在相邻两楼之间修建一个上方是一个半圆,下方是长方形的仿古通道,现有一辆卡车装满家具后,高4米,宽2.8米,请问这辆送家具的卡车能否通过这个通道?
在Rt△ABO中,OA=2米,DC=OB=1.4米,
∴AB2=22-1.42=2.04.
∵4-2.6=1.4,1.42=1.96,
2.04>1.96,
答:卡车可以通过,但要小心.
解:如图,过半圆直径的中点O,作直径的垂线交下底边于点D,取点C,使CD=1.4米,过C作OD的平行线交半圆直径于B点,交半圆于A点.
考点五 勾股定理的逆定理及其应用
例5 在△ABC中,AB=c,BC=a,AC=b, ,2c-b=12,求△ABC的面积.
解:由题意可设a=3k,则b=4k,c=5k,
∵2c-b=12,
∴10k-4k=12,
∴k=2,
∴a=6,b=8,c=10,
∵62+82=102,
∴a2+b2=c2,
∴△ABC为直角三角形,
∴△ABC的面积为 ×6×8=24.
考点六 勾股定理与折叠问题
例6 如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,求△ABE的面积.
解:∵长方形折叠,使点B与点D重合,
∴ED=BE.
设AE=xcm,则ED=BE=(9-x)cm,
在Rt△ABE中,
AB2+AE2=BE2,
∴32+x2=(9-x)2,
解得x=4.
∴△ABE的面积为3×4× =6(cm2).
方法总结
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
考点七 勾股定理特殊做题方法
例7 在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16.
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.∴BC=BD+CD=25,
∴△ABC的周长为25+20+15=60.
方法总结
勾股定理可以直接解决直角三角形中已知两边求第三边的问题;如果只知一边和另两边的关系时,也可用勾股定理求出未知边,这时往往要列出方程求解.
当高AD在△ABC外部时,如图②.
同理可得 BD=16,CD=9.
∴BC=BD-CD=7,
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
针对训练
2 有一圆柱体高为8cm,底面圆的半径为2cm,如图.在AA1上的点Q处有一只蜘蛛,QA1=3cm,在BB1上的点P处有一只苍蝇,PB=2cm.求蜘蛛爬行的最短路径长(π取3).
解:如图,沿AA1剪开,过Q作QM⊥BB1于M,连接QP.
则PM=8-3-2=3(cm),
QM=A1B1= ×2×π×2=6(cm),
在Rt△QMP中,由勾股定理得
答:蜘蛛爬行的最短路径长是 cm.
当堂练习
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
