专题2.1 认识无理数 课件(共37张PPT)
文档属性
| 名称 | 专题2.1 认识无理数 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 08:37:16 | ||
图片预览




文档简介
(共37张PPT)
八上数学同步精优课件
北师大版八年级上册
第二章 实数
2.1 认识无理数
精优教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、理解无理数的概念和其存在的意义,学会无理数的表示;
2、掌握常见的无理数类型,可以判断一个数是否是无理数;
导入新课
温故知新
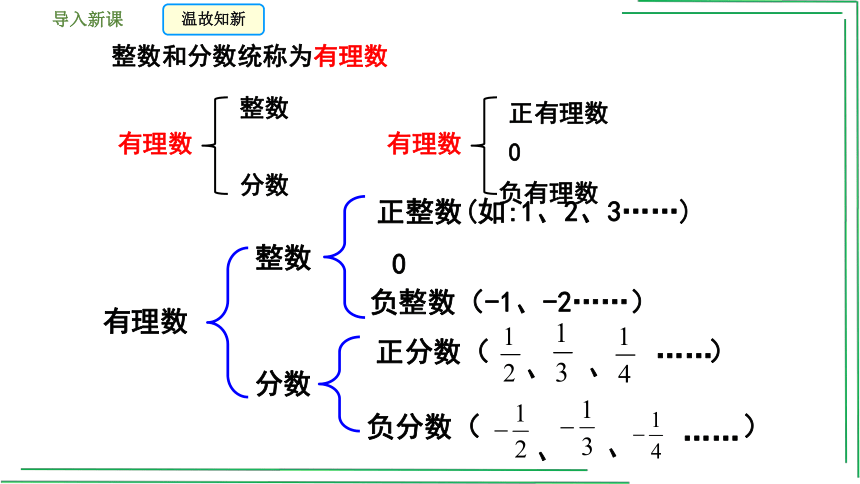
整数和分数统称为有理数
有理数
整数
分数
有理数
正有理数
负有理数
0
有理数
整数
正整数(如:1、2、3……)
0
负整数(-1、-2……)
分数
正分数( )
负分数( )
……
……
、
、
、
、
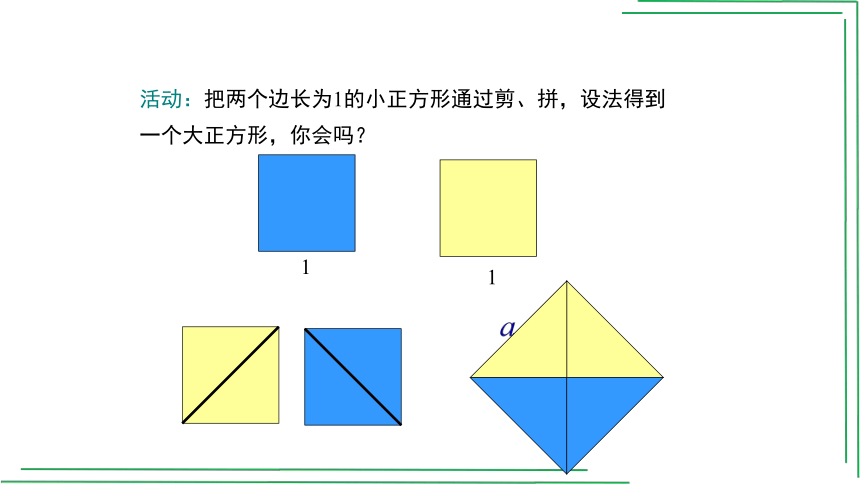
活动:把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
1
1
1
1
小清是刚升入八年级的新生,一个周末的上午,当工程师的爸爸给小红出了一道数学题:一个边长为6cm的正方形木板,按如图的痕迹锯掉四个一样的直角三角形.请计算剩下的正方形木板的面积是多少?剩下的正方形木板的边长又是多少厘米呢?见过这个数吗?你能帮小清解决这个问题吗?
2
讲授新课
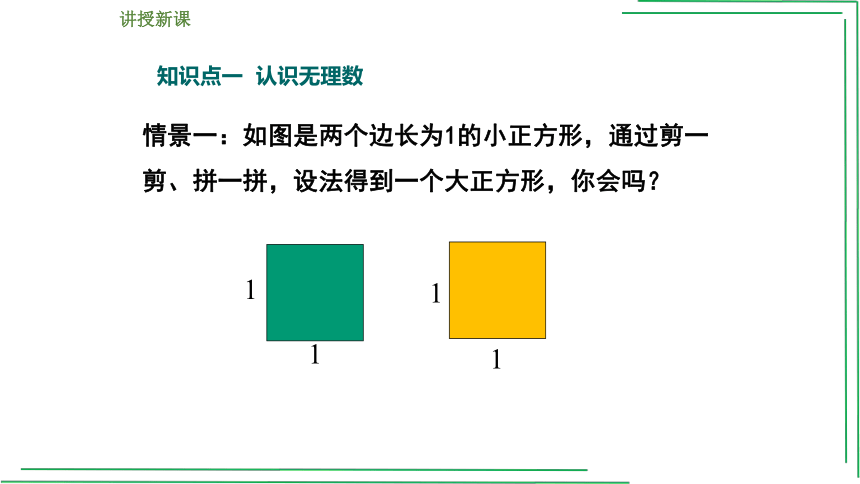
知识点一 认识无理数
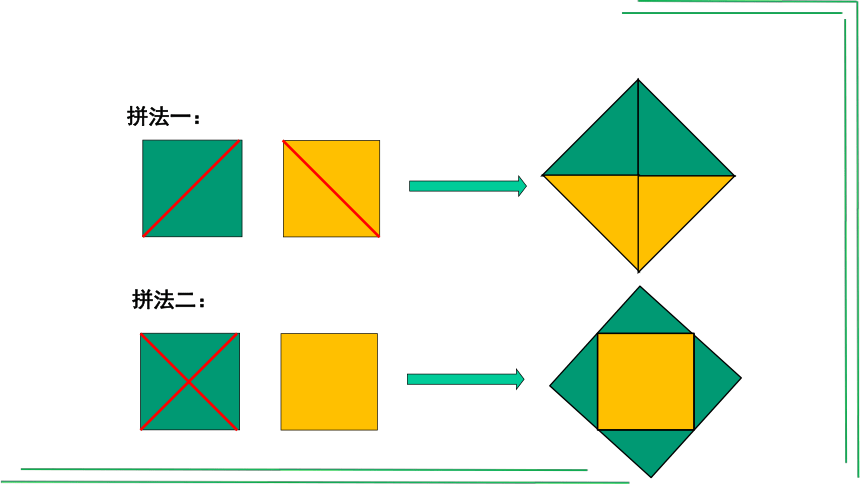
情景一:如图是两个边长为1的小正方形,通过剪一剪、拼一拼,设法得到一个大正方形,你会吗?
1
1
1
1
拼法一:
拼法二:
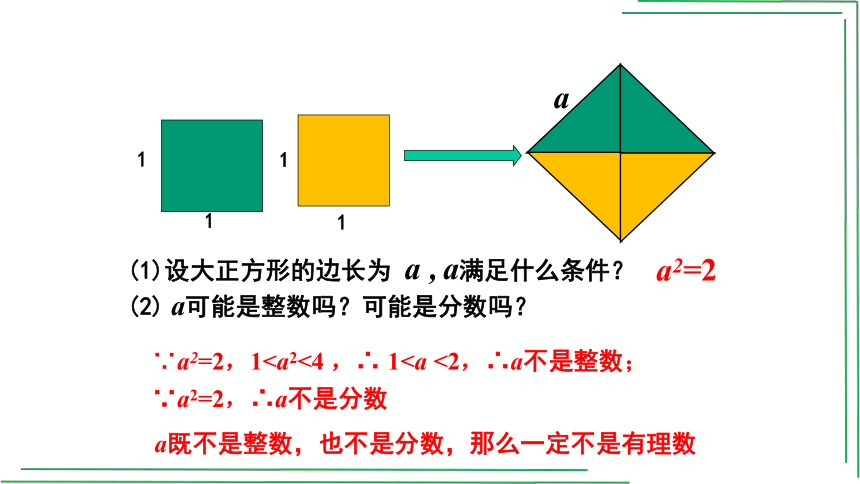
(1)设大正方形的边长为 a , a满足什么条件?
(2) a可能是整数吗?可能是分数吗?
1
1
1
1
a
a2=2
∵a2=2,1∵a2=2,∴a不是分数
a既不是整数,也不是分数,那么一定不是有理数
1
2
1
2
1
2
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
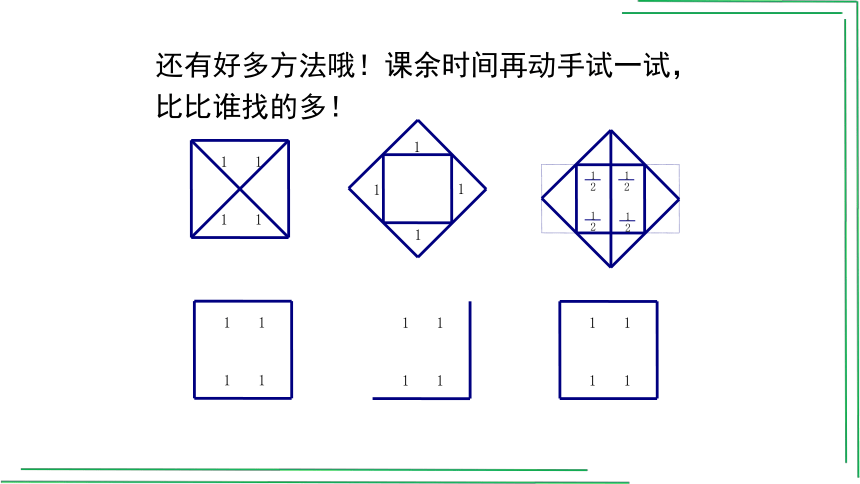
还有好多方法哦!课余时间再动手试一试,比比谁找的多!
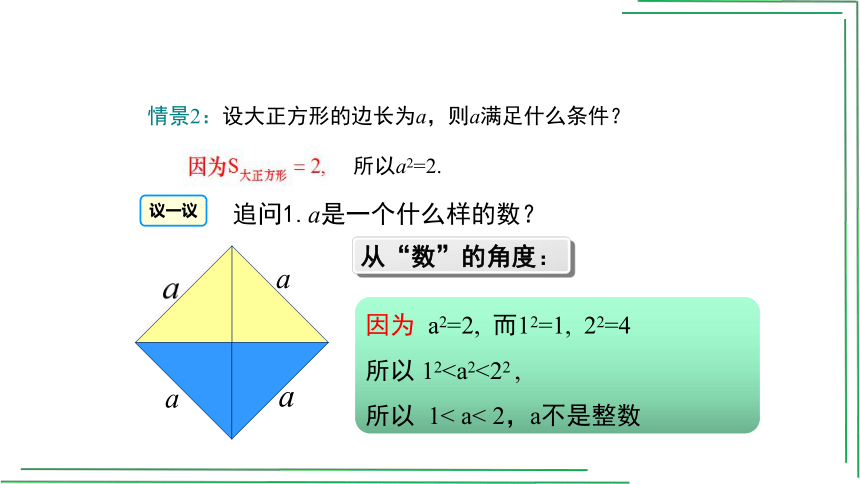
情景2:设大正方形的边长为a,则a满足什么条件?
议一议
追问1.a是一个什么样的数?
所以a2=2.
从“数”的角度:
因为 a2=2, 而12=1, 22=4
所以 12所以 1< a< 2,a不是整数
B
A
C
取出一个三角形
从“形”的角度:
在三角形ABC中,AC=1,BC=1,AB=a
根据三角形的三边关系:
AC-BC< a所以0追问:a可能是分数吗?
① a是分母为2的分数吗?
② a是分母为3的分数吗?
③ a是分母为4的分数吗?
④ a是分母为多少的分数?
归纳:a既不是整数,也不是分数,所以a不是有理数.
请同学们借助计算器进行探索
边长a 面积S
11.41.411.4141.414 211.961.988 11.999 3961.999 961 64(1)边长a会不会算到某一位时,它的平方恰好等于2呢?为什么?
(2) a可能是有限小数吗?它会是一个怎样的数呢?
a=1.414 213 56…, 它是一个无限不循环小数
想一想
估计面积为5的正方形的边长b的值,结果精确到百分位.
b=2.236067978…,它也是一个无限不循环小数
做一做
问题2:使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
活动探究
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环小数为无理数.
如π=3.14159265…,
0.101 001 000 1…(两个1之间依次多1个0)
要点归纳
典例精析
无理数有:0.1010001000001….
练一练
1.下列一组数:-8,2.5,30,π, 0.161616 … ,0.6,0.080 080 008…(相邻两个8之间依次增加一个0),其中无理数有 ( )
A.0个 B.1个 C.2个 D.3个
C
根据无理数的概念即可判定;
课堂练习
1.如图,等边三角形ABC中的边长是2,高AD为h,h可能是整数吗?可能是分数吗?
2
h
A
B
C
解:在△ABC中,AD ⊥BC
∴BD=CD=1
在Rt△ABD中,由勾股定理得:
h2=22-12=3
D
h不是整数,也不是分数,不是有理数.
2.将下列的数进行分类:
-1, ,3.14,-π,3.3,0,2, ,0.181818…,0.202 002 000 2…(相邻两个2之间0的个数逐次加1).
有理数:___________________________________,
无理数:_________________________________.
-π,0.202 002 000 2…
当堂练习
课堂小结
1.无理数是无限不循环小数,
有理数是有限小数或无限循环小数.
2.任何一个有理数都可以化成分数 形式
( p≠0, p,q 为整数且互质)
而无理数则不能.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
八上数学同步精优课件
北师大版八年级上册
第二章 实数
2.1 认识无理数
精优教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、理解无理数的概念和其存在的意义,学会无理数的表示;
2、掌握常见的无理数类型,可以判断一个数是否是无理数;
导入新课
温故知新
整数和分数统称为有理数
有理数
整数
分数
有理数
正有理数
负有理数
0
有理数
整数
正整数(如:1、2、3……)
0
负整数(-1、-2……)
分数
正分数( )
负分数( )
……
……
、
、
、
、
活动:把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形,你会吗?
1
1
1
1
小清是刚升入八年级的新生,一个周末的上午,当工程师的爸爸给小红出了一道数学题:一个边长为6cm的正方形木板,按如图的痕迹锯掉四个一样的直角三角形.请计算剩下的正方形木板的面积是多少?剩下的正方形木板的边长又是多少厘米呢?见过这个数吗?你能帮小清解决这个问题吗?
2
讲授新课
知识点一 认识无理数
情景一:如图是两个边长为1的小正方形,通过剪一剪、拼一拼,设法得到一个大正方形,你会吗?
1
1
1
1
拼法一:
拼法二:
(1)设大正方形的边长为 a , a满足什么条件?
(2) a可能是整数吗?可能是分数吗?
1
1
1
1
a
a2=2
∵a2=2,1
a既不是整数,也不是分数,那么一定不是有理数
1
2
1
2
1
2
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
还有好多方法哦!课余时间再动手试一试,比比谁找的多!
情景2:设大正方形的边长为a,则a满足什么条件?
议一议
追问1.a是一个什么样的数?
所以a2=2.
从“数”的角度:
因为 a2=2, 而12=1, 22=4
所以 12
B
A
C
取出一个三角形
从“形”的角度:
在三角形ABC中,AC=1,BC=1,AB=a
根据三角形的三边关系:
AC-BC< a
① a是分母为2的分数吗?
② a是分母为3的分数吗?
③ a是分母为4的分数吗?
④ a是分母为多少的分数?
归纳:a既不是整数,也不是分数,所以a不是有理数.
请同学们借助计算器进行探索
边长a 面积S
1
(2) a可能是有限小数吗?它会是一个怎样的数呢?
a=1.414 213 56…, 它是一个无限不循环小数
想一想
估计面积为5的正方形的边长b的值,结果精确到百分位.
b=2.236067978…,它也是一个无限不循环小数
做一做
问题2:使用计算器计算,把下列有理数写成小数的形式,你有什么发现?
活动探究
事实上,任何一个有理数都可以写成有限小数或无限循环小数.
反过来,任何有限小数或无限循环小数也都是有理数.
无限不循环小数为无理数.
如π=3.14159265…,
0.101 001 000 1…(两个1之间依次多1个0)
要点归纳
典例精析
无理数有:0.1010001000001….
练一练
1.下列一组数:-8,2.5,30,π, 0.161616 … ,0.6,0.080 080 008…(相邻两个8之间依次增加一个0),其中无理数有 ( )
A.0个 B.1个 C.2个 D.3个
C
根据无理数的概念即可判定;
课堂练习
1.如图,等边三角形ABC中的边长是2,高AD为h,h可能是整数吗?可能是分数吗?
2
h
A
B
C
解:在△ABC中,AD ⊥BC
∴BD=CD=1
在Rt△ABD中,由勾股定理得:
h2=22-12=3
D
h不是整数,也不是分数,不是有理数.
2.将下列的数进行分类:
-1, ,3.14,-π,3.3,0,2, ,0.181818…,0.202 002 000 2…(相邻两个2之间0的个数逐次加1).
有理数:___________________________________,
无理数:_________________________________.
-π,0.202 002 000 2…
当堂练习
课堂小结
1.无理数是无限不循环小数,
有理数是有限小数或无限循环小数.
2.任何一个有理数都可以化成分数 形式
( p≠0, p,q 为整数且互质)
而无理数则不能.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
