2022--2023学年人教版数学九年级上册 24.3 正多边形和圆 同步练习(Word版,含解析)
文档属性
| 名称 | 2022--2023学年人教版数学九年级上册 24.3 正多边形和圆 同步练习(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 14:14:38 | ||
图片预览

文档简介
人教版 24.3 正多边形和圆
一、选择题(共14小题)
1. 如图,正六边形 的半径 ,则点 关于原点 的对称点坐标为
A. B. C. D.
2. 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 ,则螺帽边长 等于
A. B. C. D.
3. 如图,正六边形 内接于 ,半径为 ,则这个正六边形的边心距 和 的长分别为
A. , B. , C. , D. ,
4. 我们可以只用直尺和圆规作出圆的部分内接正多边形.在我们目前所学知识的范围内,下列圆的内接正多边形不可以用尺规作图作出的是
A. 正三角形 B. 正四边形 C. 正六边形 D. 正七边形
5. 下列说法正确的是
A. 正五边形是中心对称图形 B. 正十边形的每个内角是
C. 正五边形的中心角是 D. 正十边形的每个外角是
6. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为 的正六边形,则原来的纸带宽为
A. B. C. D.
7. 如图,正五边形 内接于 , 为 上的一点(点 不与点 重合),则 的度数为
A. B. C. D.
8. 下列命题中,正确的是
A. 正多边形都是中心对称图形
B. 正多边形一个内角的大小与边数成正比例
C. 正多边形一个外角的大小与边数成反比例
D. 边数大于 的正多边形的对角线长都相等
9. 如图,已知正六边形 的边长为 ,, 分别是 和 的中点, 是 上的动点,连接 ,,当 的值最小时, 与 的夹角(锐角)度数为
A. B. C. D.
10. 如图,已知 的半径为 ,则它的内接正方形的边长为
A. B. C. D.
11. 如图, 是正五边形 的外接圆,这个正五边形的边长为 ,半径为 ,边心距为 ,则下列关系式错误的是
A. B.
C. D.
12. 如图,正六边形螺帽的边长是 ,这个扳手的开口 的值应是
A. B. C. D.
13. 如图,点 为正六边形 对角线 上一点,,,则 的值是
A. B.
C. D. 随点 位置而变化
14. 如图,将边长为 的正六边形 在直线 上由图()的位置按顺时针方向向右作无滑动滚动,当 第一次滚动到图()位置时,顶点 所经过的路径的长为
A. B. C. D.
二、填空题(共5小题)
15. 如图,若以 为边长作 的内接正多边形,则这个多边形是正 边形.
16. 已知正六边形的边长为 ,那么它的边心距等于 .
17. 如图,正六边形的面积为 ,则图中阴影部分的面积为 .
18. 半径为 的圆的内接正三角形的边长为 .
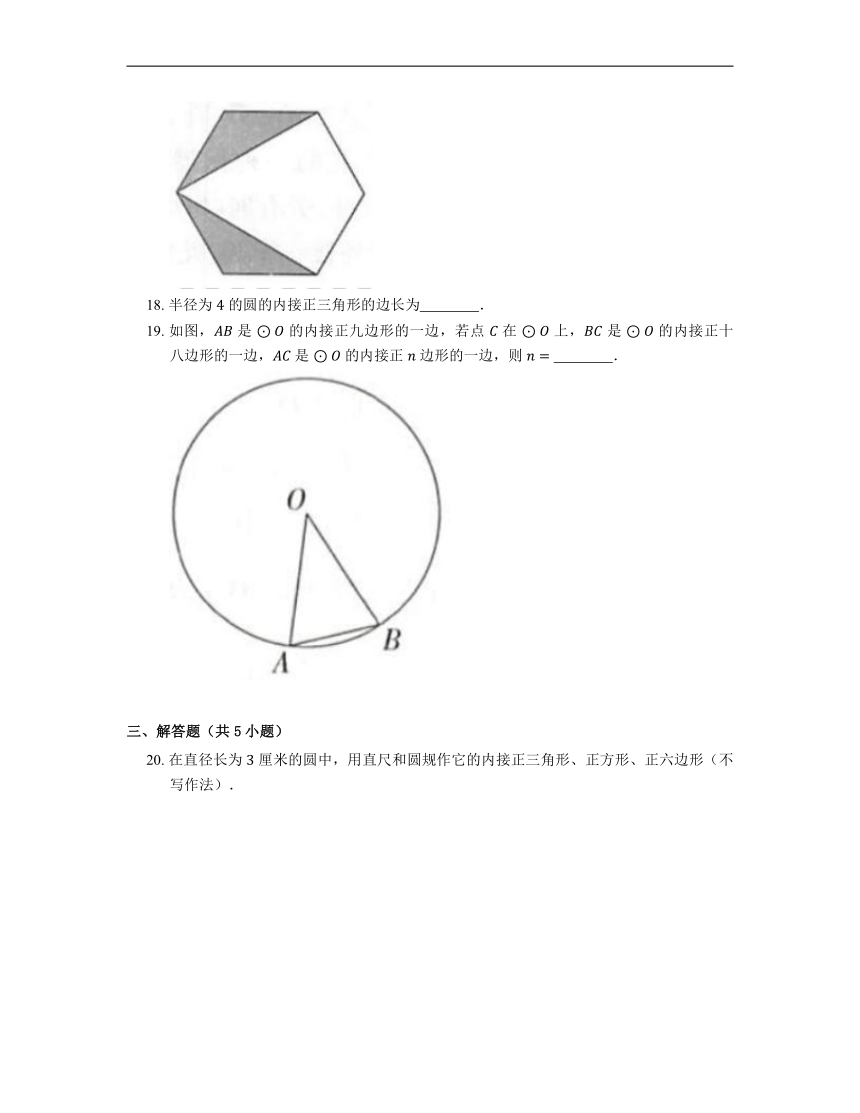
19. 如图, 是 的内接正九边形的一边,若点 在 上, 是 的内接正十八边形的一边, 是 的内接正 边形的一边,则 .
三、解答题(共5小题)
20. 在直径长为 厘米的圆中,用直尺和圆规作它的内接正三角形、正方形、正六边形(不写作法).
21. 如图,已知正五边形 .
(1)画一个五边形,使这个五边形的各角与正五边形 的各角都相等,而各边不相等.
(2)画一个五边形,使这个五边形的各边与正五边形 的各边都相等,而各角不相等.
22. 在 中,弦 是内接正十边形的一条边,弦 是内接正十五边形的一条边,那么弦 所对的圆心角是多少度 弦 是内接正几边形的一条边
23. 要在半径长为 米、圆心角为 的扇形铁皮(如图所示)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到 ).
24. 请阅读后完成证明和填空.九年级数学兴趣小组探究发现的结果,内容如下:
(1)如图 ,正三角形 中,在 , 边上分别取点 ,,使 ,连接 ,,发现 ,且 .请证明:.
(2)如图 ,正方形 中,在 , 边上分别取点 ,,使 ,连接 ,,那么 ,且 度.
(3)如图 ,正五边形 中,在 , 边上分别取点 ,,使 ,连接 ,,那么 ,且 度.
(4)在正 边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现: .
答案
1. D
【解析】如图,连接 ,
设 与 轴的交点为 .
正六边形 的半径 , 为等边三角形,
,,
,,
,,
,
点 关于原点 的对称点坐标为 .
故选D.
2. A
【解析】如图,连接 ,过点 作 于 ,
由题意得 ,,
,
由 ,得 ,
中,,
,
,即 ,
.
故选A.
3. D
【解析】连接 ,
,
,
,.
4. D
【解析】取圆上一点为圆心,以已知圆的半径为半径画弧,重复此种作法可得到圆的六等分点,据此可得圆的内接正六边形;在以上所得六等分点中,间隔取点,首尾连接可得圆的内接正三角形;由于圆的直径可以将圆二等分、两条互相垂直的直径可以将圆四等分,据此可作出圆的内接正四边形.综上可知,不可以用尺规作图作出的是圆的内接正七边形.
5. C
6. C
7. B
8. C
【解析】A.当正多边形的边数是偶数时,正多边形既是轴对称图形,也是中心对称图形,当正多边形的边数是奇数时,正多边形是轴对称图形,但不是中心对称图形,故正多边形不一定是中心对称图形,选项错误,不符合题意;
B.正多边形一个内角的大小是 ,不符合正比例的关系,故选项错误,不符合题意;
C.正多边形一个外角等于 ,正多边形一个外角的大小与它的边数成反比例;故选项正确,符合题意;
D.边数大于 的正多边形的对角线长不一定相等,故选项错误,不符合题意.
9. C
【解析】如图,连接 ,, 交 于点 ,连接 ,
正六边形 中,, 分别是 和 的中点,
直线 是正六边形的对称轴,
,
.
,
当点 与点 重合时, 的值最小.
,,
.
,
,即 .
10. D
【解析】如图所示,连接 ,,
因为 的半径为 ,四边形 是正方形,
所以 ,,
所以 .
11. A
【解析】 是正五边形 的外接圆,
,
.
在 中,;
,即 ;
,即 ;
,即 ,
关系式错误的是 .
12. A
【解析】提示:正六边形的每一个内角都是 ,边长为 ,构造直角三角形,勾股定理即可求出 的值.
13. B
14. A
15. 六
【解析】连接 .
,
是等边三角形,
,
,
这个多边形是正六边形.
16.
17.
【解析】如图,连接 ,, 交于点 .
六边形 是正六边形,
,
,,
.
18.
【解析】如图: 是等边三角形,过点 作 于 ,连接 ,,
,
是等边三角形,
,
,
,
半径为 ,
,
,
,
即直径为 的圆的内接正三角形的边长为:.
故答案为:.
19. 或
【解析】如图,
应分两种情况,
①当点 (图中 )在劣弧 上时,连接 ,
是 的内接正十八边形的一边,
.
又 是 的内接正九边形的一边,
,
,
.
②当点 (图中 )在优弧 上时,连接 ,可得 ,
.
综上所述, 的值为 或 .
20.
21. (1) 略
(2) 略
22. 弦 是内接正十边形的一条边,
弦 所对圆心角 ,
同理,弦 所对圆心角 ,
当点 在 内时,,,弦 是内接正六边形的一条边;
当点 在 外时,,,弦 是内接正三十边形的一条边.
23. 首先应考虑使正方形的各顶点在扇形的边界上,并注意扇形关于它的中心角的平分线所在直线对称,而正方形也是轴对称图形,然后分两种情况讨论:①这个正方形有两个顶点同在扇形边界的一条半径上,另外两个顶点分别在扇形边界的另一条半径和弧上;②这个正方形有两个顶点各在扇形边界的一条半径上,另外两个顶点同在扇形的弧上,在①的情况下,正方形的面积 ;在②的情况下,正方形的面积 ,于是应如①截取正方形,这时它的面积 .图略.
24. (1) 通过正三角形易证 ,可知 ,由于 ,通过外角性质得 .
(2) ;
(3) ;
(4) 正 边形内两条线段长度相等,当 时,两条线段所夹的钝角就是正 边形内角的度数,即
一、选择题(共14小题)
1. 如图,正六边形 的半径 ,则点 关于原点 的对称点坐标为
A. B. C. D.
2. 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 ,则螺帽边长 等于
A. B. C. D.
3. 如图,正六边形 内接于 ,半径为 ,则这个正六边形的边心距 和 的长分别为
A. , B. , C. , D. ,
4. 我们可以只用直尺和圆规作出圆的部分内接正多边形.在我们目前所学知识的范围内,下列圆的内接正多边形不可以用尺规作图作出的是
A. 正三角形 B. 正四边形 C. 正六边形 D. 正七边形
5. 下列说法正确的是
A. 正五边形是中心对称图形 B. 正十边形的每个内角是
C. 正五边形的中心角是 D. 正十边形的每个外角是
6. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为 的正六边形,则原来的纸带宽为
A. B. C. D.
7. 如图,正五边形 内接于 , 为 上的一点(点 不与点 重合),则 的度数为
A. B. C. D.
8. 下列命题中,正确的是
A. 正多边形都是中心对称图形
B. 正多边形一个内角的大小与边数成正比例
C. 正多边形一个外角的大小与边数成反比例
D. 边数大于 的正多边形的对角线长都相等
9. 如图,已知正六边形 的边长为 ,, 分别是 和 的中点, 是 上的动点,连接 ,,当 的值最小时, 与 的夹角(锐角)度数为
A. B. C. D.
10. 如图,已知 的半径为 ,则它的内接正方形的边长为
A. B. C. D.
11. 如图, 是正五边形 的外接圆,这个正五边形的边长为 ,半径为 ,边心距为 ,则下列关系式错误的是
A. B.
C. D.
12. 如图,正六边形螺帽的边长是 ,这个扳手的开口 的值应是
A. B. C. D.
13. 如图,点 为正六边形 对角线 上一点,,,则 的值是
A. B.
C. D. 随点 位置而变化
14. 如图,将边长为 的正六边形 在直线 上由图()的位置按顺时针方向向右作无滑动滚动,当 第一次滚动到图()位置时,顶点 所经过的路径的长为
A. B. C. D.
二、填空题(共5小题)
15. 如图,若以 为边长作 的内接正多边形,则这个多边形是正 边形.
16. 已知正六边形的边长为 ,那么它的边心距等于 .
17. 如图,正六边形的面积为 ,则图中阴影部分的面积为 .
18. 半径为 的圆的内接正三角形的边长为 .
19. 如图, 是 的内接正九边形的一边,若点 在 上, 是 的内接正十八边形的一边, 是 的内接正 边形的一边,则 .
三、解答题(共5小题)
20. 在直径长为 厘米的圆中,用直尺和圆规作它的内接正三角形、正方形、正六边形(不写作法).
21. 如图,已知正五边形 .
(1)画一个五边形,使这个五边形的各角与正五边形 的各角都相等,而各边不相等.
(2)画一个五边形,使这个五边形的各边与正五边形 的各边都相等,而各角不相等.
22. 在 中,弦 是内接正十边形的一条边,弦 是内接正十五边形的一条边,那么弦 所对的圆心角是多少度 弦 是内接正几边形的一条边
23. 要在半径长为 米、圆心角为 的扇形铁皮(如图所示)上截取一块面积尽可能大的正方形,请你设计一个截取方案(画出示意图),并计算这个正方形铁皮的面积(精确到 ).
24. 请阅读后完成证明和填空.九年级数学兴趣小组探究发现的结果,内容如下:
(1)如图 ,正三角形 中,在 , 边上分别取点 ,,使 ,连接 ,,发现 ,且 .请证明:.
(2)如图 ,正方形 中,在 , 边上分别取点 ,,使 ,连接 ,,那么 ,且 度.
(3)如图 ,正五边形 中,在 , 边上分别取点 ,,使 ,连接 ,,那么 ,且 度.
(4)在正 边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请大胆猜测,用一句话概括你的发现: .
答案
1. D
【解析】如图,连接 ,
设 与 轴的交点为 .
正六边形 的半径 , 为等边三角形,
,,
,,
,,
,
点 关于原点 的对称点坐标为 .
故选D.
2. A
【解析】如图,连接 ,过点 作 于 ,
由题意得 ,,
,
由 ,得 ,
中,,
,
,即 ,
.
故选A.
3. D
【解析】连接 ,
,
,
,.
4. D
【解析】取圆上一点为圆心,以已知圆的半径为半径画弧,重复此种作法可得到圆的六等分点,据此可得圆的内接正六边形;在以上所得六等分点中,间隔取点,首尾连接可得圆的内接正三角形;由于圆的直径可以将圆二等分、两条互相垂直的直径可以将圆四等分,据此可作出圆的内接正四边形.综上可知,不可以用尺规作图作出的是圆的内接正七边形.
5. C
6. C
7. B
8. C
【解析】A.当正多边形的边数是偶数时,正多边形既是轴对称图形,也是中心对称图形,当正多边形的边数是奇数时,正多边形是轴对称图形,但不是中心对称图形,故正多边形不一定是中心对称图形,选项错误,不符合题意;
B.正多边形一个内角的大小是 ,不符合正比例的关系,故选项错误,不符合题意;
C.正多边形一个外角等于 ,正多边形一个外角的大小与它的边数成反比例;故选项正确,符合题意;
D.边数大于 的正多边形的对角线长不一定相等,故选项错误,不符合题意.
9. C
【解析】如图,连接 ,, 交 于点 ,连接 ,
正六边形 中,, 分别是 和 的中点,
直线 是正六边形的对称轴,
,
.
,
当点 与点 重合时, 的值最小.
,,
.
,
,即 .
10. D
【解析】如图所示,连接 ,,
因为 的半径为 ,四边形 是正方形,
所以 ,,
所以 .
11. A
【解析】 是正五边形 的外接圆,
,
.
在 中,;
,即 ;
,即 ;
,即 ,
关系式错误的是 .
12. A
【解析】提示:正六边形的每一个内角都是 ,边长为 ,构造直角三角形,勾股定理即可求出 的值.
13. B
14. A
15. 六
【解析】连接 .
,
是等边三角形,
,
,
这个多边形是正六边形.
16.
17.
【解析】如图,连接 ,, 交于点 .
六边形 是正六边形,
,
,,
.
18.
【解析】如图: 是等边三角形,过点 作 于 ,连接 ,,
,
是等边三角形,
,
,
,
半径为 ,
,
,
,
即直径为 的圆的内接正三角形的边长为:.
故答案为:.
19. 或
【解析】如图,
应分两种情况,
①当点 (图中 )在劣弧 上时,连接 ,
是 的内接正十八边形的一边,
.
又 是 的内接正九边形的一边,
,
,
.
②当点 (图中 )在优弧 上时,连接 ,可得 ,
.
综上所述, 的值为 或 .
20.
21. (1) 略
(2) 略
22. 弦 是内接正十边形的一条边,
弦 所对圆心角 ,
同理,弦 所对圆心角 ,
当点 在 内时,,,弦 是内接正六边形的一条边;
当点 在 外时,,,弦 是内接正三十边形的一条边.
23. 首先应考虑使正方形的各顶点在扇形的边界上,并注意扇形关于它的中心角的平分线所在直线对称,而正方形也是轴对称图形,然后分两种情况讨论:①这个正方形有两个顶点同在扇形边界的一条半径上,另外两个顶点分别在扇形边界的另一条半径和弧上;②这个正方形有两个顶点各在扇形边界的一条半径上,另外两个顶点同在扇形的弧上,在①的情况下,正方形的面积 ;在②的情况下,正方形的面积 ,于是应如①截取正方形,这时它的面积 .图略.
24. (1) 通过正三角形易证 ,可知 ,由于 ,通过外角性质得 .
(2) ;
(3) ;
(4) 正 边形内两条线段长度相等,当 时,两条线段所夹的钝角就是正 边形内角的度数,即
同课章节目录
