1.5.3 科学记数法 课件(共25张PPT)
文档属性
| 名称 | 1.5.3 科学记数法 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 08:57:39 | ||
图片预览








文档简介
(共25张PPT)
七上数学同步精品课件
人教版七年级上册
1.5.3 科学记数法
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第一章 有理数
1.了解科学记数法的意义.
2.会用科学记数法表示较大的数.(重点、难点)
2021年天猫双11一天交易额
2021年11月12日零点,天猫双11总交易额定格在5403亿.
华为发布2021年年度报告,报告显示,华为整体经营稳健,实现全球销售收入6368亿元人民币,净利润1137亿元人民币.
天上的星星知多少?
2003年国际天文学联合会大会上,天文学家指出,整个可见宇宙空间大约有700万亿亿颗恒星,那这个数字是多少呢?它比地球上所有沙漠和海滩上的砂砾总和还要多,也就是在“7”后面加22个“0”,即约为70 000 000 000 000 000 000 000 颗.
宇宙有多大?有多少岁?
最新的研究认为宇宙的直径为1560亿光年,甚至更大.
可观测的宇宙年龄大约为138.2亿年.
第七次全国人口普查结果公布,全国人口为1443497378人.
(2)太阳的半径约为696000km.
(3)光在空气中的速度约为300000000米/秒.
在生活中我们还会遇到一些比较大的数.例如:
像这样较大的数据,书写和阅读都有一定困难,那么有没有这样一种表示方法,使得这些大数易写,易读呢
10
100
1000
10000
100000
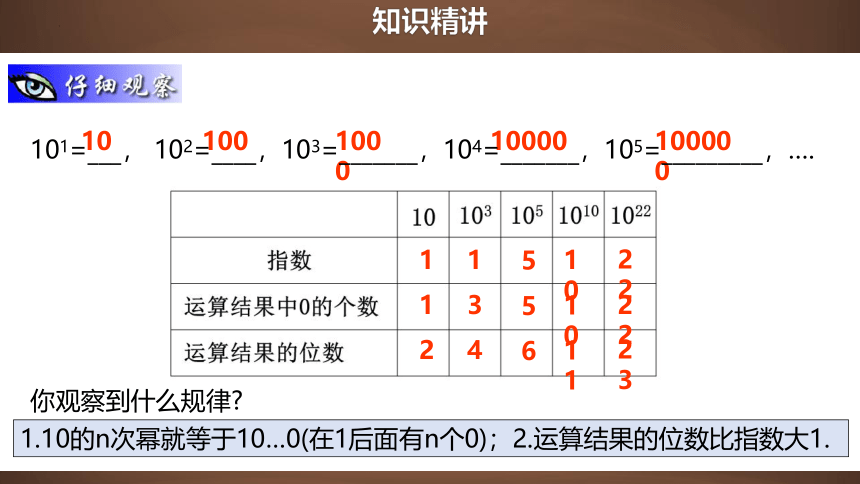
101=___, 102=____,103=_______,104=_______,105=_________,….
你观察到什么规律
1
1
5
10
22
1
3
5
10
22
2
4
6
11
23
1.10的n次幂就等于10…0(在1后面有n个0);2.运算结果的位数比指数大1.
把下列各数写成10的幂的形式.
(1)1000=____; (2)1000000=____; (3)100000000=____;
(4)10000000000=____; (5)10000000000000=____.
106
103
108
1010
1013
因此我们可以用10的乘方表示一些大数,例如:
567000000
=5.67×100000000
这样不仅可以使书写简短,同时还便于读数.
读作“5.67乘10的8次方(幂)”.
=5.67×108
像上面这样,把一个大于10的数表示成a×10n的形式(其中1≤a<10,n是正整数),使用的是科学记数法.
对于小于-10的数也可以类似科学记数法表示.
例如:
-567000000= ×100000000= .
-5.67×108
-5.67
例1.用科学记数法表示下列各数:
1000000,57000000,-123000000000
解:1000000=106,57000000=5.7×107,-123000000000=-1.23×1011
上面的式子中,等号左边整数的位数与右边10的指数有什么关系?
右边10的指数等于左边整数的位数减1.
用科学记数法表示一个n位整数,其中10的指数是_____.
n-1
用科学记数法表示下列各数:70000000000000000000000=__________;
305000000=__________;
696000=__________;
-7600000000=__________;
-560700000=_____________.
7×1022
3.05×108
6.96×105
-7.6×109
-5.607×108
例2.下列用科学记数法写出的数,原数分别是什么数?
1×107,4×103, 8.5×106, 7.04×105, -3.96×104.
解:1×107=10000000, 4×103=4000, 8.5×106=8500000,
7.04×105=704000,-3.96×104=-39600.
【点睛】反过来,如果用科学记数法表示的数10的指数是n,那么原数有n+1位整数位.
下列用科学记数法表示出来的数,原数是多少?
(1)7.2×105;(2)2.01×106;(3)5.2×102;(4)-3.07×104.
解:(1)7.2×105=720000;(2)2.01×106=2010000;
(3)5.2×102=520;(4) 3.07×104= 30700.
例3.下列各数: 9.99×109,1.01×1010,9.9×1010,1.1×1010.从小到大排列,用“<”连接起来.
解: 因为1.01<1.1<9.9
所以1.01×1010<1.1×1010<9.9×1010
因为9.99×109=9990000000,1.01×1010=10100000000
9990000000<10100000000
所以9.99×109<1.01×1010
所以9.99×109<1.01×1010<1.1×1010<9.9×1010.
比较大小: (横线.上填“>”“<”或“=”’)
(1)9.253×1010________1.002×1011
(2)5.3×105________5290000
(3)-7.83×109________-1.01×1010
>
<
<
例4.一个正常人平均心脏跳动速率为每分钟70次,请用科学记数法表示他10年(一年365天)大约跳多少次
解: 70×60×24×365×10=367920000=3.6792×108(次)
答:他10年大约跳3.6792×108次.
已知光的传播速度为300000000 m/s,太阳光到达地球的时间大约是500s,试计算太阳与地球的距离大约是多少千米.(结果用科学记数法表示)
答:太阳与地球的距离大约是1.5×108km.
解:300000000×500
=150000000000m
=150000000km
=1.5×108km
1.用科学记数法表示下列各数.
(1)340=________; (2)-3050000=____________.
2.下列各数是用科学记数法表示的数,请将它还原.
(1)1.2×107=__________;(2)-3.14×106=__________.
3.用科学记数法表示的数5.23×107原来有____位整数.
4.一种电子计算机每秒可做108次计算,用科学记数法表示它工作8分钟可做____________次计算.
3.4×104
-3.05×106
12000000
-3140000
8
4.8×1010
5.据统计,中国每年生产75亿支铅笔,需要大量木材.75亿用科学记数法表示为____________.
6.天文学里常用“光年”作为距离单位.规定1“光年”为光一-年(365天)内传播的距离,光的传播速度为3×108米/秒,则用科学记数法表示1光年=_____________千米.
7.5×109
9.4608×1012
7.2500用科学记数法表示为( )
A.0.25×104 B.2.5×103 C.2.5×102 D.25×102
8.用科学记数法记出的数5.64×106的原数是( )
A.564000 B.560000 C.5640000 D.5600000
9.据报道,某市因环境污染造成巨大经济损失,每年损失高达680万元,这个数字用科学记数法表示正确的是( )
A.6.8×102元 B.680×104元 C.6.8×106元 D.6.8×106万元
10.在下列各数中最小的为( )
A.2.13×107 B.2.1×108 C.2.2×108 D.2.31×107
B
C
C
A
11.生物学指出:生态系统中,每输入一个营养级的能量,大约只有10%的能量能够流动到下一个营养级,在H1→H2→H3→H4→H5→H6, 这条生物链中(Hn表示第n个营养级,n=1,2,…,6),要使H6获得30千焦的能量,则需要H1的提供的能量为多少千焦 (用科学记数法表示)
解:根据题意,得30×10×10×10×10×10
=3000000=3×106(千焦)
答:需要H1的提供的能量为3×106千焦.
我们可以把大于10的数记成a×10n的形式,其中a是整数数位只有一位的数(即1≤a<10), n是正整数.这种记数方法叫做科学记数法.
1.用科学计数法表示较大的数应注意以下两点:
1≤<10
当大数是大于10的整数时,n为整数位减去1.
2.灵活运用科学计数法,注意解题技巧,总结解题规律.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
七上数学同步精品课件
人教版七年级上册
1.5.3 科学记数法
情景导入
知识精讲
典例解析
针对练习
达标检测
小结梳理
第一章 有理数
1.了解科学记数法的意义.
2.会用科学记数法表示较大的数.(重点、难点)
2021年天猫双11一天交易额
2021年11月12日零点,天猫双11总交易额定格在5403亿.
华为发布2021年年度报告,报告显示,华为整体经营稳健,实现全球销售收入6368亿元人民币,净利润1137亿元人民币.
天上的星星知多少?
2003年国际天文学联合会大会上,天文学家指出,整个可见宇宙空间大约有700万亿亿颗恒星,那这个数字是多少呢?它比地球上所有沙漠和海滩上的砂砾总和还要多,也就是在“7”后面加22个“0”,即约为70 000 000 000 000 000 000 000 颗.
宇宙有多大?有多少岁?
最新的研究认为宇宙的直径为1560亿光年,甚至更大.
可观测的宇宙年龄大约为138.2亿年.
第七次全国人口普查结果公布,全国人口为1443497378人.
(2)太阳的半径约为696000km.
(3)光在空气中的速度约为300000000米/秒.
在生活中我们还会遇到一些比较大的数.例如:
像这样较大的数据,书写和阅读都有一定困难,那么有没有这样一种表示方法,使得这些大数易写,易读呢
10
100
1000
10000
100000
101=___, 102=____,103=_______,104=_______,105=_________,….
你观察到什么规律
1
1
5
10
22
1
3
5
10
22
2
4
6
11
23
1.10的n次幂就等于10…0(在1后面有n个0);2.运算结果的位数比指数大1.
把下列各数写成10的幂的形式.
(1)1000=____; (2)1000000=____; (3)100000000=____;
(4)10000000000=____; (5)10000000000000=____.
106
103
108
1010
1013
因此我们可以用10的乘方表示一些大数,例如:
567000000
=5.67×100000000
这样不仅可以使书写简短,同时还便于读数.
读作“5.67乘10的8次方(幂)”.
=5.67×108
像上面这样,把一个大于10的数表示成a×10n的形式(其中1≤a<10,n是正整数),使用的是科学记数法.
对于小于-10的数也可以类似科学记数法表示.
例如:
-567000000= ×100000000= .
-5.67×108
-5.67
例1.用科学记数法表示下列各数:
1000000,57000000,-123000000000
解:1000000=106,57000000=5.7×107,-123000000000=-1.23×1011
上面的式子中,等号左边整数的位数与右边10的指数有什么关系?
右边10的指数等于左边整数的位数减1.
用科学记数法表示一个n位整数,其中10的指数是_____.
n-1
用科学记数法表示下列各数:70000000000000000000000=__________;
305000000=__________;
696000=__________;
-7600000000=__________;
-560700000=_____________.
7×1022
3.05×108
6.96×105
-7.6×109
-5.607×108
例2.下列用科学记数法写出的数,原数分别是什么数?
1×107,4×103, 8.5×106, 7.04×105, -3.96×104.
解:1×107=10000000, 4×103=4000, 8.5×106=8500000,
7.04×105=704000,-3.96×104=-39600.
【点睛】反过来,如果用科学记数法表示的数10的指数是n,那么原数有n+1位整数位.
下列用科学记数法表示出来的数,原数是多少?
(1)7.2×105;(2)2.01×106;(3)5.2×102;(4)-3.07×104.
解:(1)7.2×105=720000;(2)2.01×106=2010000;
(3)5.2×102=520;(4) 3.07×104= 30700.
例3.下列各数: 9.99×109,1.01×1010,9.9×1010,1.1×1010.从小到大排列,用“<”连接起来.
解: 因为1.01<1.1<9.9
所以1.01×1010<1.1×1010<9.9×1010
因为9.99×109=9990000000,1.01×1010=10100000000
9990000000<10100000000
所以9.99×109<1.01×1010
所以9.99×109<1.01×1010<1.1×1010<9.9×1010.
比较大小: (横线.上填“>”“<”或“=”’)
(1)9.253×1010________1.002×1011
(2)5.3×105________5290000
(3)-7.83×109________-1.01×1010
>
<
<
例4.一个正常人平均心脏跳动速率为每分钟70次,请用科学记数法表示他10年(一年365天)大约跳多少次
解: 70×60×24×365×10=367920000=3.6792×108(次)
答:他10年大约跳3.6792×108次.
已知光的传播速度为300000000 m/s,太阳光到达地球的时间大约是500s,试计算太阳与地球的距离大约是多少千米.(结果用科学记数法表示)
答:太阳与地球的距离大约是1.5×108km.
解:300000000×500
=150000000000m
=150000000km
=1.5×108km
1.用科学记数法表示下列各数.
(1)340=________; (2)-3050000=____________.
2.下列各数是用科学记数法表示的数,请将它还原.
(1)1.2×107=__________;(2)-3.14×106=__________.
3.用科学记数法表示的数5.23×107原来有____位整数.
4.一种电子计算机每秒可做108次计算,用科学记数法表示它工作8分钟可做____________次计算.
3.4×104
-3.05×106
12000000
-3140000
8
4.8×1010
5.据统计,中国每年生产75亿支铅笔,需要大量木材.75亿用科学记数法表示为____________.
6.天文学里常用“光年”作为距离单位.规定1“光年”为光一-年(365天)内传播的距离,光的传播速度为3×108米/秒,则用科学记数法表示1光年=_____________千米.
7.5×109
9.4608×1012
7.2500用科学记数法表示为( )
A.0.25×104 B.2.5×103 C.2.5×102 D.25×102
8.用科学记数法记出的数5.64×106的原数是( )
A.564000 B.560000 C.5640000 D.5600000
9.据报道,某市因环境污染造成巨大经济损失,每年损失高达680万元,这个数字用科学记数法表示正确的是( )
A.6.8×102元 B.680×104元 C.6.8×106元 D.6.8×106万元
10.在下列各数中最小的为( )
A.2.13×107 B.2.1×108 C.2.2×108 D.2.31×107
B
C
C
A
11.生物学指出:生态系统中,每输入一个营养级的能量,大约只有10%的能量能够流动到下一个营养级,在H1→H2→H3→H4→H5→H6, 这条生物链中(Hn表示第n个营养级,n=1,2,…,6),要使H6获得30千焦的能量,则需要H1的提供的能量为多少千焦 (用科学记数法表示)
解:根据题意,得30×10×10×10×10×10
=3000000=3×106(千焦)
答:需要H1的提供的能量为3×106千焦.
我们可以把大于10的数记成a×10n的形式,其中a是整数数位只有一位的数(即1≤a<10), n是正整数.这种记数方法叫做科学记数法.
1.用科学计数法表示较大的数应注意以下两点:
1≤<10
当大数是大于10的整数时,n为整数位减去1.
2.灵活运用科学计数法,注意解题技巧,总结解题规律.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
