北师大版七年级数学下册1.4整式的乘法 同步练习 (word版 含解析)
文档属性
| 名称 | 北师大版七年级数学下册1.4整式的乘法 同步练习 (word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 357.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 14:36:30 | ||
图片预览


文档简介
北师大版 1.4 整式的乘法
一、选择题(共9小题)
1. 的计算结果是
A. B. C. D.
2. 若等式 成立,则 填写单项式可以是
A. B. C. D.
3. 多项式 与 的积不含一次项,则 的值为
A. B. C. D.
4. 下列计算正确的是
A.
B.
C.
D.
5. 若 ,则 , 的值分别是
A. , B. , C. , D. ,
6. 以下计算正确的是
A. B.
C. D.
7. 若 ,则 , 的值分别为
A. , B. , C. , D. ,
8. 下列运算正确的是
A. B.
C. D.
9. 若 的展开式中不含 项,则
A. B. C. D.
二、填空题(共6小题)
10. 单项式乘单项式法则:
单项式与单项式相乘,把它们的 , 分别相乘的积作为 ,其余字母连同它的 不变,也作为积的因式.
11. 单项式乘多项式法则:
单项式与多项式相乘,用 乘以 的每一项,再把所得的积 ;即: .
12. .
13. 单项式与单项式相乘的法则,对于三项以上的单项式 也适用.
14. 单项式与多项式的乘积仍是一个 ,结果在没有化简前项数与原多项式的 相同.
15. 计算: .
三、解答题(共6小题)
16. 已知一个长方体的长为 ,宽为 ,高为 .
(1)用 , 的代数式来表示该长方体的体积与表面积.
(2)当 , 时,求相应长方体的体积与表面积.
17. 小明在计算一个多项式乘 时,因抄错运算符号,写成了加上 ,结果算成 ,那么原题正确的计算结果是什么 请计算出正确的结果.
18. 如图,现有一块长为(3a+b)米,宽为(a+2b)米的长方形地块,规划将阴影部分进行绿化,中间预留部分是边长为a米的正方形.
(1)求绿化的面积(用含a,b的代数式表示);
(2)若a=3,b=1,绿化成本为50元/平方米,则完成绿化共需要多少元
19. 计算:
(1);
(2).
20. 若 ,求 的值.
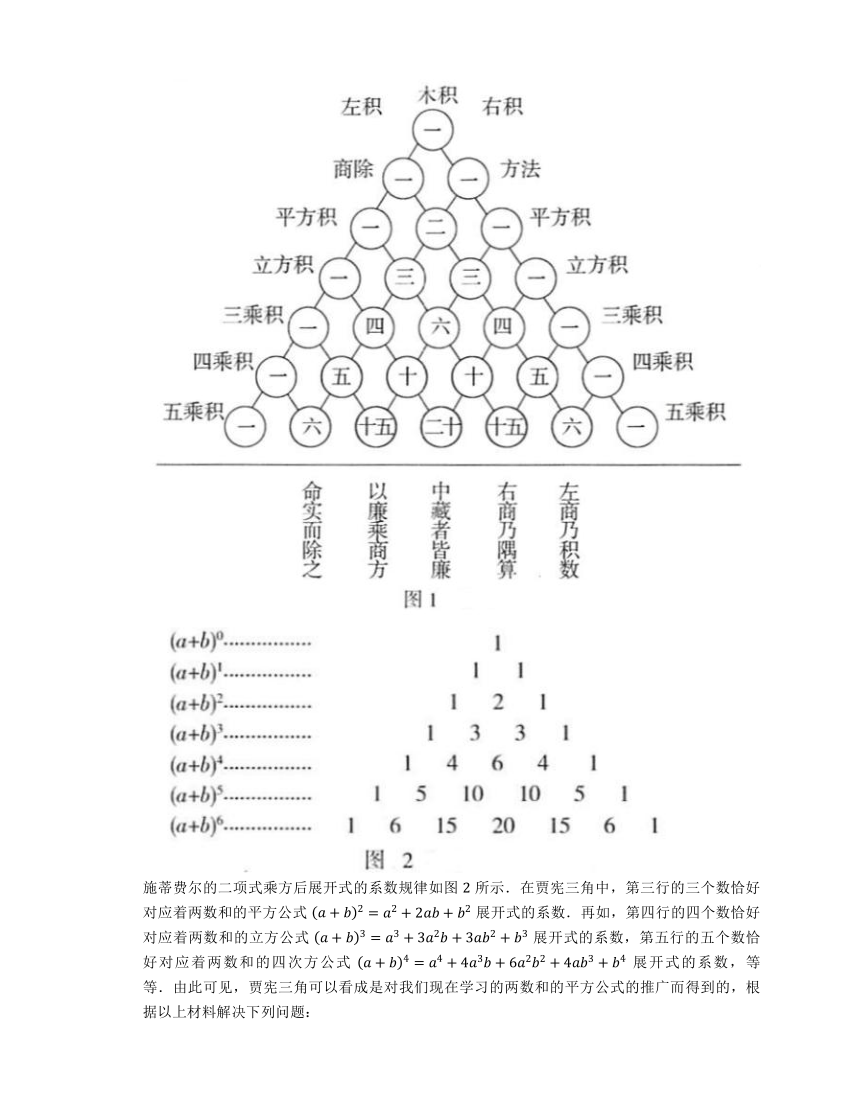
21. 贾宪三角(如图 )最初于 世纪被发现,原图记载于我国北宋时期数学家贾宪的《黄帝九章算法细草》一书中,原名“开方作法本源图”,用来作开方运算,在数学史上占有领先地位.我国南宋时期数学家杨辉对此有着记载之功,他于 年写下的《详解九章算法》一书中记载着这一图表.因此,后人把这个图表称作贾宪三角或杨辉三角.
施蒂费尔的二项式乘方后展开式的系数规律如图 所示.在贾宪三角中,第三行的三个数恰好对应着两数和的平方公式 展开式的系数.再如,第四行的四个数恰好对应着两数和的立方公式 展开式的系数,第五行的五个数恰好对应着两数和的四次方公式 展开式的系数,等等.由此可见,贾宪三角可以看成是对我们现在学习的两数和的平方公式的推广而得到的,根据以上材料解决下列问题:
(1) 展开式中项数共有 项;
(2)写出 的展开式: ;
(3)计算:
(4)若 ,求 的值.
答案
1. C
【解析】.
2. C
【解析】 等式 成立,
,
填写单项式可以是:.
3. B
4. C
5. B
6. D
【解析】,A计算错误;
与 不能合并,B项计算错误;
,C项计算错误.
故选D.
7. D
8. C
【解析】因为 ,
所以选项A不符合题意;
因为 ,
所以选项B不符合题意;
因为 ,
所以选项C符合题意;
因为 ,
所以选项D不符合题意.
9. B
【解析】,
不含 ,
,
,
故选:B.
10. 系数,同底数幂,积的因式,指数
11. 单项式,多项式,相加,
12.
13. 相乘
14. 多项式,项数
15.
16. (1) ;.
(2) ;.
17. 原多项式 ,
所以正确的结果为 .
18. (1) 长方形的面积 , 预留部分面积 , 则绿化的面积
【解析】略
(2) 当a=3,b=1时,绿化的面积=2×9+7×3×1+2=41(平方米),41×50=2050(元).
【解析】略
19. (1)
(2)
20.
21. (1)
(2)
(3)
(4) 当 时,,
当 时,,
.、
一、选择题(共9小题)
1. 的计算结果是
A. B. C. D.
2. 若等式 成立,则 填写单项式可以是
A. B. C. D.
3. 多项式 与 的积不含一次项,则 的值为
A. B. C. D.
4. 下列计算正确的是
A.
B.
C.
D.
5. 若 ,则 , 的值分别是
A. , B. , C. , D. ,
6. 以下计算正确的是
A. B.
C. D.
7. 若 ,则 , 的值分别为
A. , B. , C. , D. ,
8. 下列运算正确的是
A. B.
C. D.
9. 若 的展开式中不含 项,则
A. B. C. D.
二、填空题(共6小题)
10. 单项式乘单项式法则:
单项式与单项式相乘,把它们的 , 分别相乘的积作为 ,其余字母连同它的 不变,也作为积的因式.
11. 单项式乘多项式法则:
单项式与多项式相乘,用 乘以 的每一项,再把所得的积 ;即: .
12. .
13. 单项式与单项式相乘的法则,对于三项以上的单项式 也适用.
14. 单项式与多项式的乘积仍是一个 ,结果在没有化简前项数与原多项式的 相同.
15. 计算: .
三、解答题(共6小题)
16. 已知一个长方体的长为 ,宽为 ,高为 .
(1)用 , 的代数式来表示该长方体的体积与表面积.
(2)当 , 时,求相应长方体的体积与表面积.
17. 小明在计算一个多项式乘 时,因抄错运算符号,写成了加上 ,结果算成 ,那么原题正确的计算结果是什么 请计算出正确的结果.
18. 如图,现有一块长为(3a+b)米,宽为(a+2b)米的长方形地块,规划将阴影部分进行绿化,中间预留部分是边长为a米的正方形.
(1)求绿化的面积(用含a,b的代数式表示);
(2)若a=3,b=1,绿化成本为50元/平方米,则完成绿化共需要多少元
19. 计算:
(1);
(2).
20. 若 ,求 的值.
21. 贾宪三角(如图 )最初于 世纪被发现,原图记载于我国北宋时期数学家贾宪的《黄帝九章算法细草》一书中,原名“开方作法本源图”,用来作开方运算,在数学史上占有领先地位.我国南宋时期数学家杨辉对此有着记载之功,他于 年写下的《详解九章算法》一书中记载着这一图表.因此,后人把这个图表称作贾宪三角或杨辉三角.
施蒂费尔的二项式乘方后展开式的系数规律如图 所示.在贾宪三角中,第三行的三个数恰好对应着两数和的平方公式 展开式的系数.再如,第四行的四个数恰好对应着两数和的立方公式 展开式的系数,第五行的五个数恰好对应着两数和的四次方公式 展开式的系数,等等.由此可见,贾宪三角可以看成是对我们现在学习的两数和的平方公式的推广而得到的,根据以上材料解决下列问题:
(1) 展开式中项数共有 项;
(2)写出 的展开式: ;
(3)计算:
(4)若 ,求 的值.
答案
1. C
【解析】.
2. C
【解析】 等式 成立,
,
填写单项式可以是:.
3. B
4. C
5. B
6. D
【解析】,A计算错误;
与 不能合并,B项计算错误;
,C项计算错误.
故选D.
7. D
8. C
【解析】因为 ,
所以选项A不符合题意;
因为 ,
所以选项B不符合题意;
因为 ,
所以选项C符合题意;
因为 ,
所以选项D不符合题意.
9. B
【解析】,
不含 ,
,
,
故选:B.
10. 系数,同底数幂,积的因式,指数
11. 单项式,多项式,相加,
12.
13. 相乘
14. 多项式,项数
15.
16. (1) ;.
(2) ;.
17. 原多项式 ,
所以正确的结果为 .
18. (1) 长方形的面积 , 预留部分面积 , 则绿化的面积
【解析】略
(2) 当a=3,b=1时,绿化的面积=2×9+7×3×1+2=41(平方米),41×50=2050(元).
【解析】略
19. (1)
(2)
20.
21. (1)
(2)
(3)
(4) 当 时,,
当 时,,
.、
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
