北师大版数学九年级下册 1.6利用三角函数测高 同步练习(Word版,含解析)
文档属性
| 名称 | 北师大版数学九年级下册 1.6利用三角函数测高 同步练习(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 14:38:37 | ||
图片预览



文档简介
北师大版 1.6 利用三角函数测高
一、选择题(共12小题)
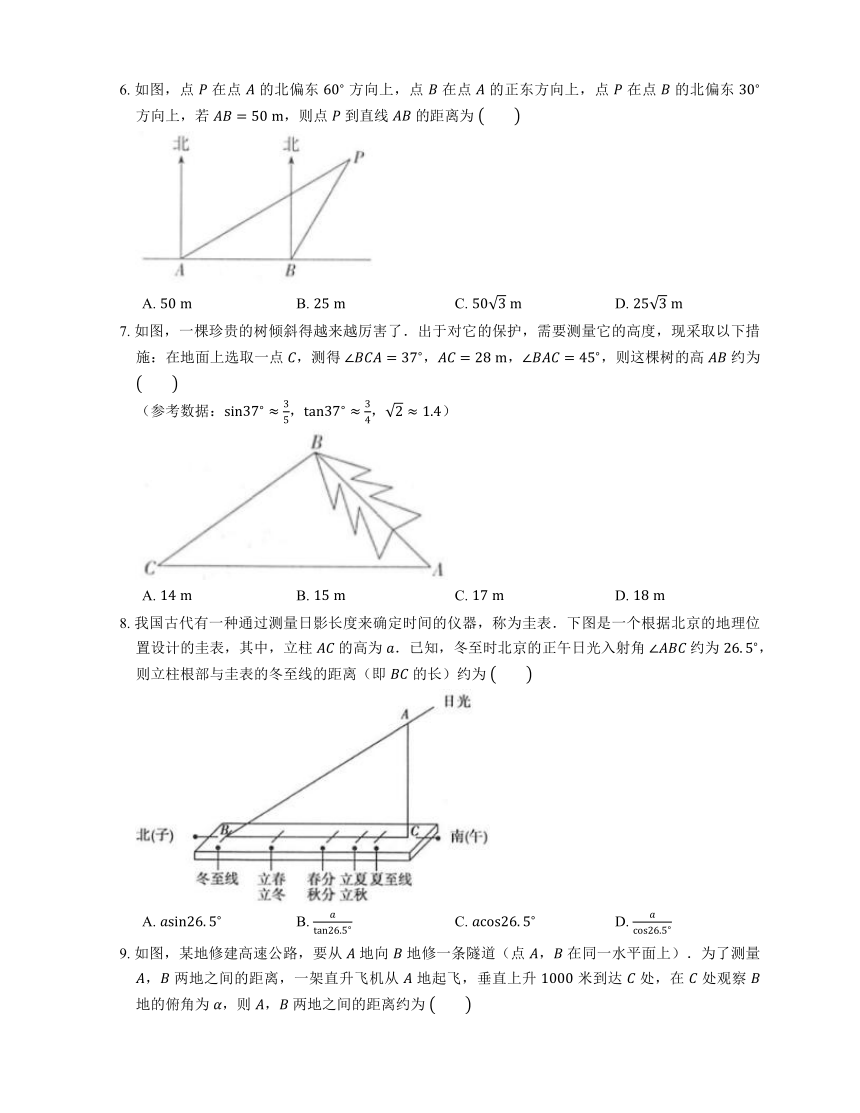
1. 直角梯形 如图放置,, 为水平线,,如果 ,从低处 处看高处 处,那么点 在点 的
A. 俯角 方向 B. 俯角 方向 C. 仰角 方向 D. 仰角 方向
2. 如果在 处观察 处时的仰角为 ,那么在 处观察 处时的俯角为
A. B. C. D.
3. 小新站在高楼上的点 处看一棵小树顶端 的仰角为 ,同时看小树底端 的俯角为 ,则 等于
A. B. C. D.
4. 如图,从点 观测点 的仰角是
A. B. C. D.
5. 如图,小明想要测量学校操场上旗杆 的高度,他做了如下操作:()在点 处放置测角仪,测得旗杆顶的仰角 ;()量得测角仪的高度 ;()量得测角仪到旗杆的水平距离 .利用锐角三角函数及解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
6. 如图,点 在点 的北偏东 方向上,点 在点 的正东方向上,点 在点 的北偏东 方向上,若 ,则点 到直线 的距离为
A. B. C. D.
7. 如图,一棵珍贵的树倾斜得越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点 ,测得 ,,,则这棵树的高 约为
(参考数据:,,)
A. B. C. D.
8. 我国古代有一种通过测量日影长度来确定时间的仪器,称为圭表.下图是一个根据北京的地理位置设计的圭表,其中,立柱 的高为 .已知,冬至时北京的正午日光入射角 约为 ,则立柱根部与圭表的冬至线的距离(即 的长)约为
A. B. C. D.
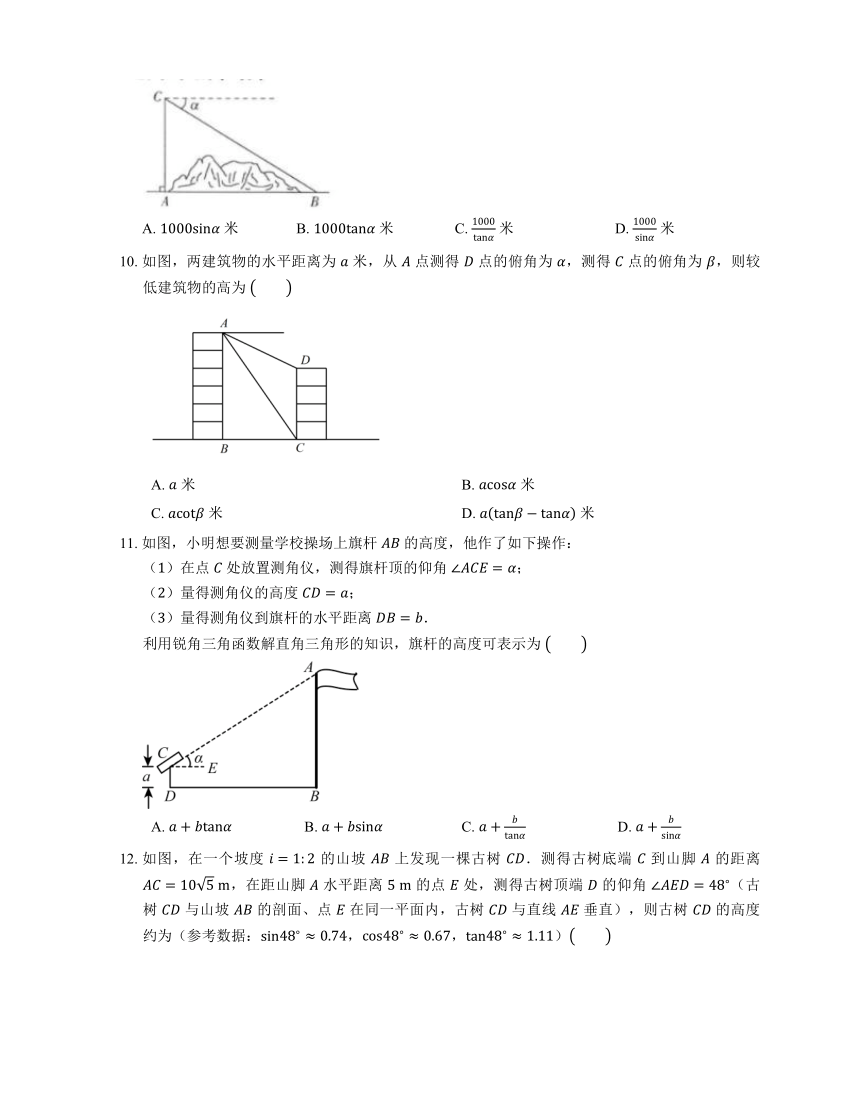
9. 如图,某地修建高速公路,要从 地向 地修一条隧道(点 , 在同一水平面上).为了测量 , 两地之间的距离,一架直升飞机从 地起飞,垂直上升 米到达 处,在 处观察 地的俯角为 ,则 , 两地之间的距离约为
A. 米 B. 米 C. 米 D. 米
10. 如图,两建筑物的水平距离为 米,从 点测得 点的俯角为 ,测得 点的俯角为 ,则较低建筑物的高为
A. 米 B. 米
C. 米 D. 米
11. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:
()在点 处放置测角仪,测得旗杆顶的仰角 ;
()量得测角仪的高度 ;
()量得测角仪到旗杆的水平距离 .
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
12. 如图,在一个坡度 的山坡 上发现一棵古树 .测得古树底端 到山脚 的距离 ,在距山脚 水平距离 的点 处,测得古树顶端 的仰角 (古树 与山坡 的剖面、点 在同一平面内,古树 与直线 垂直),则古树 的高度约为(参考数据:,,)
A. B. C. D.
二、填空题(共5小题)
13. 如图,航拍无人机从 处测得一幢建筑物顶部 的仰角为 ,测得底部 的俯角为 ,此时航拍无人机与该建筑物的水平距离 为 米,那么该建筑物的高度 约为 米.(精确到 米,参考数据:)
14. 如果在 点处观察 点的仰角为 ,那么在 点处观察 点的俯角为 .(用含 的式子表示)
15. 小明要测量公园里一棵古树的高,被一条小溪挡住去路,采用计算方法,在 点测得古树顶的仰角为 ,向前走了 米到 点,测得古树顶的仰角为 ,则古树的高度为 米.
16. 如图,在量角器的圆心 处下挂一铅锤,制作了一个简易测倾仪,从量角器的点 处观测,当量角器的 刻度线 对准旗杆顶端时,铅垂线对应的度数是 ,则此时观测旗杆顶端的仰角度数是 .
17. 已知某小山坡的坡长为 米、山坡的高度为 米,那么该山坡的坡度 .
三、解答题(共6小题)
18. 如图所示,课外活动中,小明在离旗杆 米的 处,用测角仪测得旗杆顶部 的仰角为 ,已知测角仪器的高 米,求旗杆 的高.(精确到 米)
(供选用的数据:,,)
19. 如图是某校体育场内一看台的截面图,看台 与水平线的夹角为 ,最低处 与地面的距离 为 米,在 , 正前方有垂直于地面的旗杆 ,在 , 两处测得旗杆顶端 的仰角分别为 和 , 长为 米,升旗仪式中,当国歌开始播放时,国旗也在离地面 米的 处同时冉冉升起,国歌播放结束时,国旗刚好上升到旗杆顶端 ,已知国歌播放时间为 秒,求国旗上升的平均速度.(结果精确到 米/秒)
20. 如图,在某海滨城市 附近海面有一股台风,据监测,当前台风中心位于该城市的南偏东 方向 千米的海面 处,并以 千米/时的速度向 处的北偏西 的方向移动,台风侵袭范围是一个圆形区域,当前半径为 千米,且圆的半径以 千米/时速度不断扩张.
(参考数据 ,)
(1)当台风中心移动 小时时,受台风侵袭的圆形区域半径增大到 千米;当台风中心移动 小时时,受台风侵袭的圆形区域半径增大到 千米;
(2)当台风中心移动到与城市 距离最近时,这股台风是否侵袭这座海滨城市 请说明理由.
21. 如图,在东西方向的海岸线 上有一长为 千米的码头 ,在距码头西端 的正西方向 千米处有一观测站 ,现测得位于观测站 的北偏西 方向,且与观测站 相距 千米的小岛 处有艘轮船开始航行驶向港口 .经过一段时间后又测得该轮船位于观测站 的正北方向,且与观测站 相距 千米的 处.
(参考数据:,,)
(1)求 两地的距离(结果保留根号);
(2)如果该轮船不改变航向继续航行,那么轮船能否行至码头 靠岸 请说明理由.
22. 如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端 、 的距离,飞机以距海平面垂直同一高度飞行,在点 处测得端点 的俯角为 ,然后沿着平行于 的方向水平飞行了 米,在点 测得端点 的俯角为 ,已知岛屿两端 、 的距离 米,求飞机飞行的高度.(结果精确到 米,参考数据:,)
23. 如图 是一种自卸货车,图 是该货车的示意图,货箱侧面是一个矩形,长 米,宽 米,初始时点 ,, 在同一水平线上,车厢底部 离地面的高度为 米.卸货时货箱在千斤顶的作用下绕着点 旋转,箱体底部 形成不同角度的斜坡.
(精确到 米,参考值:,,,)
(1)当斜坡 坡角为 时,求车厢最高点 离地面的距离;
(2)点 处的转轴与后车轮转轴(点 处)的水平距离叫做安全轴距,已知该车的安全轴距为 .货厢对角线 , 的交点 是货厢侧面的重心,卸货时如果 , 两点的水平距离小于安全轴距时,会发生车辆倾覆安全事故.当斜坡 的坡角为 时,根据上述车辆设计技术参数,该货车会发生车辆倾覆安全事故吗 试说明你的理由.
答案
1. D
【解析】,,
,
从低处 处看高处 处,那么点 在点 的仰角 方向.
2. A
【解析】设 , 两点的水平线分别为 ,,
依题意,得 ,,
由平行线的性质可知,.
3. B
4. B
【解析】 从点 观测点 的视线是 ,水平线是 ,
从点 观测点 的仰角是 .
5. A
【解析】过 作 于 ,
则四边形 是矩形,
,,
,
,
.
6. D
【解析】作 于点 ,
由题意得 ,.
在 中,,
,
在 中,,
,
由题意得 ,
解得 ,
即点 到直线 的距离为 .
故选D.
7. C
【解析】如图,作 于点 .
设 ,
,,
.
,
,
,
,
.
8. B
【解析】因为 ,
所以 .
9. C
【解析】由题意可知 米,.
,
米.
10. D
【解析】作 于点 .
在直角 中,,,
,
所以 ,
同理,.
.
11. A 【解析】过 作 于 ,则四边形 是矩形.
,,
,
,
,
.
12. A
【解析】如图,延长 交直线 于点 ,
由题意可知,,,
,
,
.
在 中,,
由勾股定理,得 ,即 ,
,,
.
在 中,,
,即 ,解得 ,
即古树 的高度约为 .
故选A.
13.
【解析】由题意可得:,
解得:,
同理,.
故该建筑物的高度为:.
14.
15.
【解析】如图, 为树高,点 为树顶,则 ,,,
依题意,有
由①得
把③代入②,解得 .
故答案为:.
16.
17.
【解析】由勾股定理可知山坡的水平距离为: 米,
坡度 .
18. ,,,
四边形 是矩形,
米,
在 中,
米,,
(米),
(米).
答:旗杆 的高是 米.
19. 依题意得 ,.
在 中,.
在 中,.
.
.
答:国旗上升的平均速度约为 米/秒.
20. (1) ;
【解析】由题意可得,当台风中心移动 小时时,受台风侵袭的圆形区域半径增大到:(千米),
当台风中心移动 小时时,受台风侵袭的圆形区域半径增大到:(千米).
(2) 作 于点 ,
, 点在 点南偏东 ,
与南北方向夹角是 , 点在 点北偏西 ,
与南北方向夹角是 ,
,
在等腰直角三角形 中, 千米,
根据勾股定理可算得 (千米),
设经过 小时时,台风中心从 移动到 ,
则 ,解得 (小时),
此时,受台风侵袭地区的圆的半径为:(千米)(千米),
城市 不会受到侵袭.
21. (1) 过点 作 于点 .
由题意,得 ,,,,
,,
,
.
(2) 如果该轮船不改变航向继续航行,那么轮船不能行至码头 靠岸.
延长 交 于 ,
,
,
,
,解得 ,
,,
,
,
如果该轮船不改变航向继续航行,那么轮船不能行至码头 靠岸.
22. 过点 作 于点 ,过点 作 于点 ,
设高度为 米.
因为 ,
所以 ,
所以四边形 为矩形.
所以 ,.
由题意可知: 米, 米.
在 中,,
所以 (米).
在 中,,
所以 (米).
所以 ,即 .
解得:.
答:飞机行飞行的高度是 米.
23. (1) 如图,过点 , 作 ,,垂足分别为 ,, 交 于点 ,过点 作 于点 ,
则四边形 是矩形,
,
,,
,
斜坡 的坡角为 ,即 ,
,
,,
,,,,
.
(2) 该货车不会发生车辆倾覆安全事故,理由如下,
如图,过点 作 于点 ,
同理求得 ,
在 中,,,
,
四边形 是矩形,
,
,
,
,
,
该货车不会发生车辆倾覆安全事故.
一、选择题(共12小题)
1. 直角梯形 如图放置,, 为水平线,,如果 ,从低处 处看高处 处,那么点 在点 的
A. 俯角 方向 B. 俯角 方向 C. 仰角 方向 D. 仰角 方向
2. 如果在 处观察 处时的仰角为 ,那么在 处观察 处时的俯角为
A. B. C. D.
3. 小新站在高楼上的点 处看一棵小树顶端 的仰角为 ,同时看小树底端 的俯角为 ,则 等于
A. B. C. D.
4. 如图,从点 观测点 的仰角是
A. B. C. D.
5. 如图,小明想要测量学校操场上旗杆 的高度,他做了如下操作:()在点 处放置测角仪,测得旗杆顶的仰角 ;()量得测角仪的高度 ;()量得测角仪到旗杆的水平距离 .利用锐角三角函数及解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
6. 如图,点 在点 的北偏东 方向上,点 在点 的正东方向上,点 在点 的北偏东 方向上,若 ,则点 到直线 的距离为
A. B. C. D.
7. 如图,一棵珍贵的树倾斜得越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点 ,测得 ,,,则这棵树的高 约为
(参考数据:,,)
A. B. C. D.
8. 我国古代有一种通过测量日影长度来确定时间的仪器,称为圭表.下图是一个根据北京的地理位置设计的圭表,其中,立柱 的高为 .已知,冬至时北京的正午日光入射角 约为 ,则立柱根部与圭表的冬至线的距离(即 的长)约为
A. B. C. D.
9. 如图,某地修建高速公路,要从 地向 地修一条隧道(点 , 在同一水平面上).为了测量 , 两地之间的距离,一架直升飞机从 地起飞,垂直上升 米到达 处,在 处观察 地的俯角为 ,则 , 两地之间的距离约为
A. 米 B. 米 C. 米 D. 米
10. 如图,两建筑物的水平距离为 米,从 点测得 点的俯角为 ,测得 点的俯角为 ,则较低建筑物的高为
A. 米 B. 米
C. 米 D. 米
11. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:
()在点 处放置测角仪,测得旗杆顶的仰角 ;
()量得测角仪的高度 ;
()量得测角仪到旗杆的水平距离 .
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为
A. B. C. D.
12. 如图,在一个坡度 的山坡 上发现一棵古树 .测得古树底端 到山脚 的距离 ,在距山脚 水平距离 的点 处,测得古树顶端 的仰角 (古树 与山坡 的剖面、点 在同一平面内,古树 与直线 垂直),则古树 的高度约为(参考数据:,,)
A. B. C. D.
二、填空题(共5小题)
13. 如图,航拍无人机从 处测得一幢建筑物顶部 的仰角为 ,测得底部 的俯角为 ,此时航拍无人机与该建筑物的水平距离 为 米,那么该建筑物的高度 约为 米.(精确到 米,参考数据:)
14. 如果在 点处观察 点的仰角为 ,那么在 点处观察 点的俯角为 .(用含 的式子表示)
15. 小明要测量公园里一棵古树的高,被一条小溪挡住去路,采用计算方法,在 点测得古树顶的仰角为 ,向前走了 米到 点,测得古树顶的仰角为 ,则古树的高度为 米.
16. 如图,在量角器的圆心 处下挂一铅锤,制作了一个简易测倾仪,从量角器的点 处观测,当量角器的 刻度线 对准旗杆顶端时,铅垂线对应的度数是 ,则此时观测旗杆顶端的仰角度数是 .
17. 已知某小山坡的坡长为 米、山坡的高度为 米,那么该山坡的坡度 .
三、解答题(共6小题)
18. 如图所示,课外活动中,小明在离旗杆 米的 处,用测角仪测得旗杆顶部 的仰角为 ,已知测角仪器的高 米,求旗杆 的高.(精确到 米)
(供选用的数据:,,)
19. 如图是某校体育场内一看台的截面图,看台 与水平线的夹角为 ,最低处 与地面的距离 为 米,在 , 正前方有垂直于地面的旗杆 ,在 , 两处测得旗杆顶端 的仰角分别为 和 , 长为 米,升旗仪式中,当国歌开始播放时,国旗也在离地面 米的 处同时冉冉升起,国歌播放结束时,国旗刚好上升到旗杆顶端 ,已知国歌播放时间为 秒,求国旗上升的平均速度.(结果精确到 米/秒)
20. 如图,在某海滨城市 附近海面有一股台风,据监测,当前台风中心位于该城市的南偏东 方向 千米的海面 处,并以 千米/时的速度向 处的北偏西 的方向移动,台风侵袭范围是一个圆形区域,当前半径为 千米,且圆的半径以 千米/时速度不断扩张.
(参考数据 ,)
(1)当台风中心移动 小时时,受台风侵袭的圆形区域半径增大到 千米;当台风中心移动 小时时,受台风侵袭的圆形区域半径增大到 千米;
(2)当台风中心移动到与城市 距离最近时,这股台风是否侵袭这座海滨城市 请说明理由.
21. 如图,在东西方向的海岸线 上有一长为 千米的码头 ,在距码头西端 的正西方向 千米处有一观测站 ,现测得位于观测站 的北偏西 方向,且与观测站 相距 千米的小岛 处有艘轮船开始航行驶向港口 .经过一段时间后又测得该轮船位于观测站 的正北方向,且与观测站 相距 千米的 处.
(参考数据:,,)
(1)求 两地的距离(结果保留根号);
(2)如果该轮船不改变航向继续航行,那么轮船能否行至码头 靠岸 请说明理由.
22. 如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端 、 的距离,飞机以距海平面垂直同一高度飞行,在点 处测得端点 的俯角为 ,然后沿着平行于 的方向水平飞行了 米,在点 测得端点 的俯角为 ,已知岛屿两端 、 的距离 米,求飞机飞行的高度.(结果精确到 米,参考数据:,)
23. 如图 是一种自卸货车,图 是该货车的示意图,货箱侧面是一个矩形,长 米,宽 米,初始时点 ,, 在同一水平线上,车厢底部 离地面的高度为 米.卸货时货箱在千斤顶的作用下绕着点 旋转,箱体底部 形成不同角度的斜坡.
(精确到 米,参考值:,,,)
(1)当斜坡 坡角为 时,求车厢最高点 离地面的距离;
(2)点 处的转轴与后车轮转轴(点 处)的水平距离叫做安全轴距,已知该车的安全轴距为 .货厢对角线 , 的交点 是货厢侧面的重心,卸货时如果 , 两点的水平距离小于安全轴距时,会发生车辆倾覆安全事故.当斜坡 的坡角为 时,根据上述车辆设计技术参数,该货车会发生车辆倾覆安全事故吗 试说明你的理由.
答案
1. D
【解析】,,
,
从低处 处看高处 处,那么点 在点 的仰角 方向.
2. A
【解析】设 , 两点的水平线分别为 ,,
依题意,得 ,,
由平行线的性质可知,.
3. B
4. B
【解析】 从点 观测点 的视线是 ,水平线是 ,
从点 观测点 的仰角是 .
5. A
【解析】过 作 于 ,
则四边形 是矩形,
,,
,
,
.
6. D
【解析】作 于点 ,
由题意得 ,.
在 中,,
,
在 中,,
,
由题意得 ,
解得 ,
即点 到直线 的距离为 .
故选D.
7. C
【解析】如图,作 于点 .
设 ,
,,
.
,
,
,
,
.
8. B
【解析】因为 ,
所以 .
9. C
【解析】由题意可知 米,.
,
米.
10. D
【解析】作 于点 .
在直角 中,,,
,
所以 ,
同理,.
.
11. A 【解析】过 作 于 ,则四边形 是矩形.
,,
,
,
,
.
12. A
【解析】如图,延长 交直线 于点 ,
由题意可知,,,
,
,
.
在 中,,
由勾股定理,得 ,即 ,
,,
.
在 中,,
,即 ,解得 ,
即古树 的高度约为 .
故选A.
13.
【解析】由题意可得:,
解得:,
同理,.
故该建筑物的高度为:.
14.
15.
【解析】如图, 为树高,点 为树顶,则 ,,,
依题意,有
由①得
把③代入②,解得 .
故答案为:.
16.
17.
【解析】由勾股定理可知山坡的水平距离为: 米,
坡度 .
18. ,,,
四边形 是矩形,
米,
在 中,
米,,
(米),
(米).
答:旗杆 的高是 米.
19. 依题意得 ,.
在 中,.
在 中,.
.
.
答:国旗上升的平均速度约为 米/秒.
20. (1) ;
【解析】由题意可得,当台风中心移动 小时时,受台风侵袭的圆形区域半径增大到:(千米),
当台风中心移动 小时时,受台风侵袭的圆形区域半径增大到:(千米).
(2) 作 于点 ,
, 点在 点南偏东 ,
与南北方向夹角是 , 点在 点北偏西 ,
与南北方向夹角是 ,
,
在等腰直角三角形 中, 千米,
根据勾股定理可算得 (千米),
设经过 小时时,台风中心从 移动到 ,
则 ,解得 (小时),
此时,受台风侵袭地区的圆的半径为:(千米)(千米),
城市 不会受到侵袭.
21. (1) 过点 作 于点 .
由题意,得 ,,,,
,,
,
.
(2) 如果该轮船不改变航向继续航行,那么轮船不能行至码头 靠岸.
延长 交 于 ,
,
,
,
,解得 ,
,,
,
,
如果该轮船不改变航向继续航行,那么轮船不能行至码头 靠岸.
22. 过点 作 于点 ,过点 作 于点 ,
设高度为 米.
因为 ,
所以 ,
所以四边形 为矩形.
所以 ,.
由题意可知: 米, 米.
在 中,,
所以 (米).
在 中,,
所以 (米).
所以 ,即 .
解得:.
答:飞机行飞行的高度是 米.
23. (1) 如图,过点 , 作 ,,垂足分别为 ,, 交 于点 ,过点 作 于点 ,
则四边形 是矩形,
,
,,
,
斜坡 的坡角为 ,即 ,
,
,,
,,,,
.
(2) 该货车不会发生车辆倾覆安全事故,理由如下,
如图,过点 作 于点 ,
同理求得 ,
在 中,,,
,
四边形 是矩形,
,
,
,
,
,
该货车不会发生车辆倾覆安全事故.
