北师大版九年级数学下册 2.3 确定二次函数的表达式 同步练习(Word版,含解析)
文档属性
| 名称 | 北师大版九年级数学下册 2.3 确定二次函数的表达式 同步练习(Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 464.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 14:44:53 | ||
图片预览


文档简介
北师大版 2.3 确定二次函数的表达式
一、选择题(共8小题)
1. 将抛物线 化为顶点式 的形式为
A. B.
C. D.
2. 已知 与 的关系如表所示,若设 ,则下列选项中, 与 之间的函数关系式正确的是
A. B. C. D.
3. 已知抛物线 的顶点在 轴上,则 等于
A. B. C. D.
4. 把 化成 的形式是
A. B.
C. D.
5. 二次函数 的图象经过点 ,则代数式 的值为
A. B. C. D.
6. 将二次函数 化成 的形式是
A. B.
C. D.
7. 将二次函数 用配方法化成 的形式,下列结果中正确的是
A. B.
C. D.
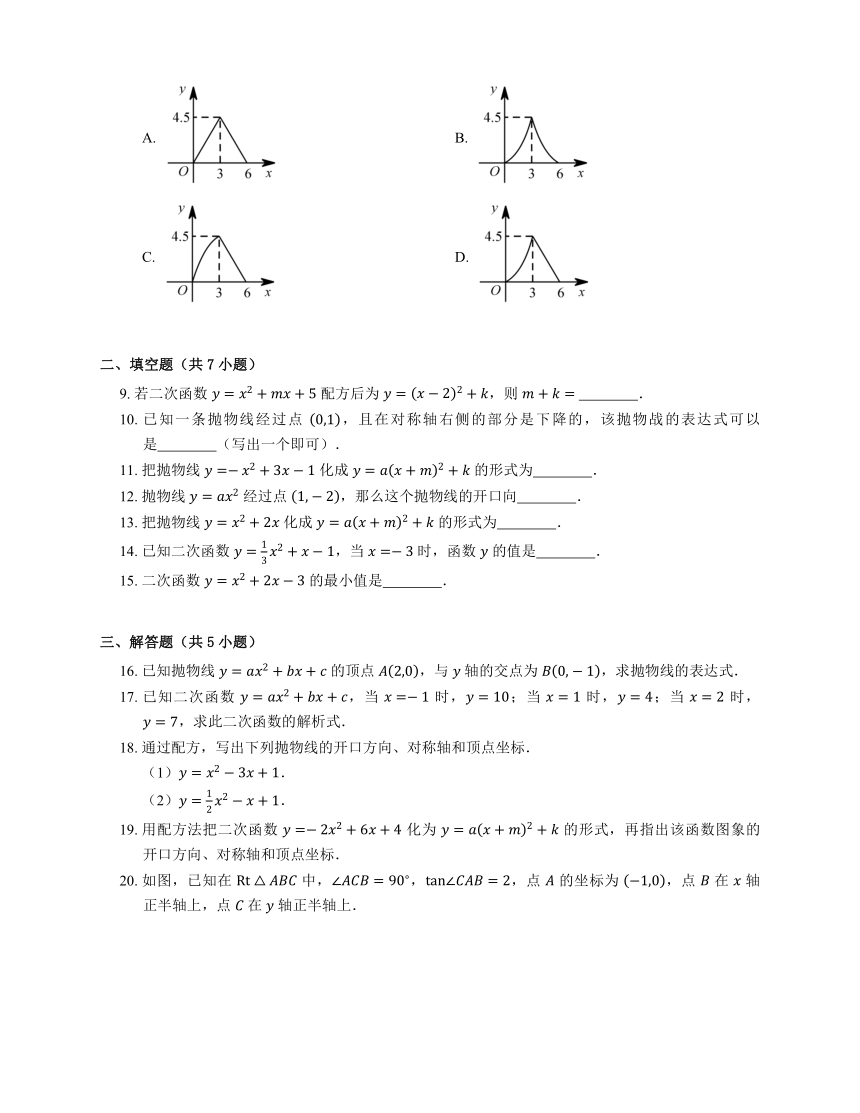
8. 如图,在 中,,,动点 从点 出发,以 的速度沿 方向运动到点 ,动点 同时从点 出发,以 的速度沿折线 方向运动到点 .设 的面积为 (),运动时间为 (),则下列图象能反映 与 之间关系的是
A. B.
C. D.
二、填空题(共7小题)
9. 若二次函数 配方后为 ,则 .
10. 已知一条抛物线经过点 ,且在对称轴右侧的部分是下降的,该抛物战的表达式可以是 (写出一个即可).
11. 把抛物线 化成 的形式为 .
12. 抛物线 经过点 ,那么这个抛物线的开口向 .
13. 把抛物线 化成 的形式为 .
14. 已知二次函数 ,当 时,函数 的值是 .
15. 二次函数 的最小值是 .
三、解答题(共5小题)
16. 已知抛物线 的顶点 ,与 轴的交点为 ,求抛物线的表达式.
17. 已知二次函数 ,当 时,;当 时,;当 时,,求此二次函数的解析式.
18. 通过配方,写出下列抛物线的开口方向、对称轴和顶点坐标.
(1).
(2).
19. 用配方法把二次函数 化为 的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.
20. 如图,已知在 中,,,点 的坐标为 ,点 在 轴正半轴上,点 在 轴正半轴上.
(1)求经过 , 两点的直线的表达式.
(2)求图象经过 ,, 三点的二次函数的解析式.
答案
1. B
2. A
【解析】将题表中的三组值分别代入 中,可得 ,,,所以 与 之间的函数关系式为 .
3. D
4. D
5. B
【解析】 二次函数 的图象经过点 ,
.
.
.
6. A
7. C
【解析】.
8. D
【解析】过点 作 于点 ,
①如图 ,
当点 在 上运动时,即 ,
由题意知 ,,
,
,
则 ;
②如图 ,
当点 在 上运动时,即 ,此时点 与点 重合,
由题意知 ,,
,
,
则 .
9.
10.
【解析】 在对称轴右侧部分是下降,
设抛物线的解析式可以为 ,
经过点 ,
解析式可以是 .
11.
12. 下
【解析】 抛物线 经过点 ,
,
,
这个抛物线的开口向下.
13.
14.
【解析】当 时,.
15.
16. 因为抛物线的顶点是 ,
所以设抛物线的表达式为 .
由抛物线过 ,得 ,
所以 ,
所以抛物线的表达式为 ,
即 .
17. .
18. (1) 开口向上,顶点 ,对称轴为直线 .
(2) 开口向下,顶点 ,对称轴为直线 .
19.
开口向下,对称轴为直线 ,顶点 .
20. (1) ,点 的坐标为 ,,
,则 ,,
,,
,
,,
,,
,
设直线 为:,
解得:
直线 为:.
(2) 设过 ,, 的抛物线为:,
,
解得:,
抛物线为:.
一、选择题(共8小题)
1. 将抛物线 化为顶点式 的形式为
A. B.
C. D.
2. 已知 与 的关系如表所示,若设 ,则下列选项中, 与 之间的函数关系式正确的是
A. B. C. D.
3. 已知抛物线 的顶点在 轴上,则 等于
A. B. C. D.
4. 把 化成 的形式是
A. B.
C. D.
5. 二次函数 的图象经过点 ,则代数式 的值为
A. B. C. D.
6. 将二次函数 化成 的形式是
A. B.
C. D.
7. 将二次函数 用配方法化成 的形式,下列结果中正确的是
A. B.
C. D.
8. 如图,在 中,,,动点 从点 出发,以 的速度沿 方向运动到点 ,动点 同时从点 出发,以 的速度沿折线 方向运动到点 .设 的面积为 (),运动时间为 (),则下列图象能反映 与 之间关系的是
A. B.
C. D.
二、填空题(共7小题)
9. 若二次函数 配方后为 ,则 .
10. 已知一条抛物线经过点 ,且在对称轴右侧的部分是下降的,该抛物战的表达式可以是 (写出一个即可).
11. 把抛物线 化成 的形式为 .
12. 抛物线 经过点 ,那么这个抛物线的开口向 .
13. 把抛物线 化成 的形式为 .
14. 已知二次函数 ,当 时,函数 的值是 .
15. 二次函数 的最小值是 .
三、解答题(共5小题)
16. 已知抛物线 的顶点 ,与 轴的交点为 ,求抛物线的表达式.
17. 已知二次函数 ,当 时,;当 时,;当 时,,求此二次函数的解析式.
18. 通过配方,写出下列抛物线的开口方向、对称轴和顶点坐标.
(1).
(2).
19. 用配方法把二次函数 化为 的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.
20. 如图,已知在 中,,,点 的坐标为 ,点 在 轴正半轴上,点 在 轴正半轴上.
(1)求经过 , 两点的直线的表达式.
(2)求图象经过 ,, 三点的二次函数的解析式.
答案
1. B
2. A
【解析】将题表中的三组值分别代入 中,可得 ,,,所以 与 之间的函数关系式为 .
3. D
4. D
5. B
【解析】 二次函数 的图象经过点 ,
.
.
.
6. A
7. C
【解析】.
8. D
【解析】过点 作 于点 ,
①如图 ,
当点 在 上运动时,即 ,
由题意知 ,,
,
,
则 ;
②如图 ,
当点 在 上运动时,即 ,此时点 与点 重合,
由题意知 ,,
,
,
则 .
9.
10.
【解析】 在对称轴右侧部分是下降,
设抛物线的解析式可以为 ,
经过点 ,
解析式可以是 .
11.
12. 下
【解析】 抛物线 经过点 ,
,
,
这个抛物线的开口向下.
13.
14.
【解析】当 时,.
15.
16. 因为抛物线的顶点是 ,
所以设抛物线的表达式为 .
由抛物线过 ,得 ,
所以 ,
所以抛物线的表达式为 ,
即 .
17. .
18. (1) 开口向上,顶点 ,对称轴为直线 .
(2) 开口向下,顶点 ,对称轴为直线 .
19.
开口向下,对称轴为直线 ,顶点 .
20. (1) ,点 的坐标为 ,,
,则 ,,
,,
,
,,
,,
,
设直线 为:,
解得:
直线 为:.
(2) 设过 ,, 的抛物线为:,
,
解得:,
抛物线为:.
