人教版数学九年级上册 24.1.3 弧、弦、圆心角 课件(共33张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.1.3 弧、弦、圆心角 课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 14:50:54 | ||
图片预览









文档简介
(共33张PPT)
24.1.3 弧、弦、圆心角
谢 谢!
令令令令令令
★顶点在
,并且两边都与圆相交的
角叫做
★圆心角、弧、弦之间的关系
(1)由圆的旋转对称性可知:在
中,相等的圆心角所对的弧
,所对的弦也
(2)在
中,如果两个圆心角、两
条弧或两条弦中有一组量相等,那么它们对应的其
余各组量都分别相等.
考点(①
利用定理与推论进行证明
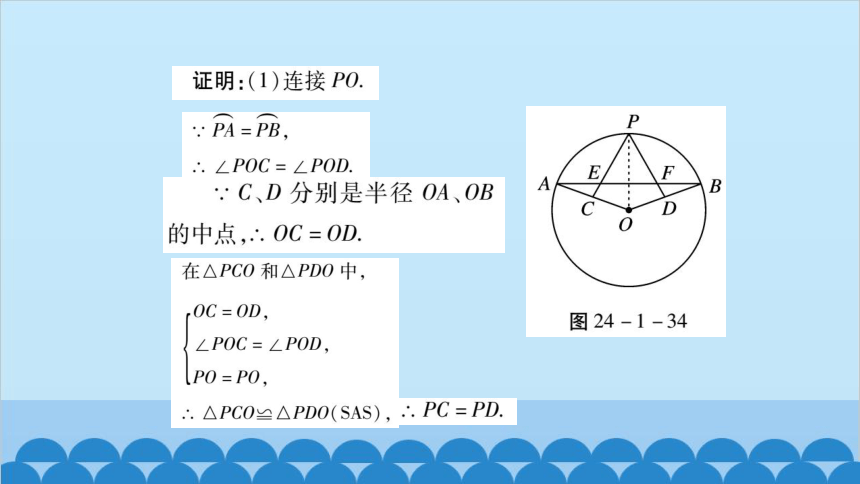
例1
如图24-1-34,PA=PB,C、D分别是
半径OA、OB的中点,连接PC、PD,交弦AB于E、F两
点.求证:
(1PC=PD;
(2PE=PF.
P
E
A
F
B
C
D
图24-1-34
在△PCO和△PD0中,
0C=0D,
∠POC=∠POD,
P0=P0,
∴.△PC0≌△PDO(SAS),
方法总结
在同圆或等圆中,要证弦、孤、圆心
角及弦心距中的一组量相等,通常可以将其转化为证
另外三组量中的一组量相等,一般有多种证法,而连
半径或作垂直于弦的直径构造等弦、等孤、等圆心角、
等弦心距是常用的作辅助线的方法:
1.下列命题:
①相等的圆心角所对的弦不一定相等;
②圆心角不相等,所对的弦就不相等;
③相等的弦所对的圆心角相等;
④两条弧不相等,它们所对的圆心角有可能相等;
⑤两条弧不相等,它们所对的弦就不相等.
其中真命题有
(
A.0个
B.1个
C.2个
D.3个
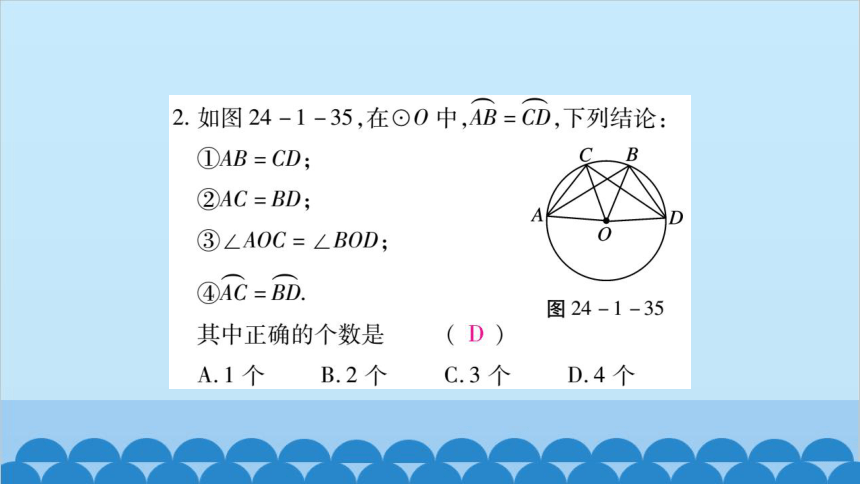
2.如图24-1-35,在⊙0中,AB=CD,下列结论:
①AB=CD;
B
②AC=BD;
A
3∠AOC=∠BOD:
④AC=BD.
图24-1-35
其中正确的个数是
(
A.1个
B.2个
C.3个
D.4个
3.如图24-1-36,P为直径AB上一点,EF、CD为
过点P的两条弦,且∠DPB=∠EPB.求证:
(1CD=EF;
(2)CE =DF.
E
C
A
0
B
F
D
图24-1-36
E
C
M
A
B
N
F
D
1.下列说法正确的是
A.等弦所对的弧相等
B.等弧对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
3.如图24-1-42,过△ABC的三个顶点作圆,将
△ABC绕圆心O逆时针方向旋转°(0<α<
90),得到△A'B'C'.若AB'=A'C=CB,则∠B的
度数为
(
A.30°
B.45
C.50°
D.60°
24.1.3 弧、弦、圆心角
谢 谢!
令令令令令令
★顶点在
,并且两边都与圆相交的
角叫做
★圆心角、弧、弦之间的关系
(1)由圆的旋转对称性可知:在
中,相等的圆心角所对的弧
,所对的弦也
(2)在
中,如果两个圆心角、两
条弧或两条弦中有一组量相等,那么它们对应的其
余各组量都分别相等.
考点(①
利用定理与推论进行证明
例1
如图24-1-34,PA=PB,C、D分别是
半径OA、OB的中点,连接PC、PD,交弦AB于E、F两
点.求证:
(1PC=PD;
(2PE=PF.
P
E
A
F
B
C
D
图24-1-34
在△PCO和△PD0中,
0C=0D,
∠POC=∠POD,
P0=P0,
∴.△PC0≌△PDO(SAS),
方法总结
在同圆或等圆中,要证弦、孤、圆心
角及弦心距中的一组量相等,通常可以将其转化为证
另外三组量中的一组量相等,一般有多种证法,而连
半径或作垂直于弦的直径构造等弦、等孤、等圆心角、
等弦心距是常用的作辅助线的方法:
1.下列命题:
①相等的圆心角所对的弦不一定相等;
②圆心角不相等,所对的弦就不相等;
③相等的弦所对的圆心角相等;
④两条弧不相等,它们所对的圆心角有可能相等;
⑤两条弧不相等,它们所对的弦就不相等.
其中真命题有
(
A.0个
B.1个
C.2个
D.3个
2.如图24-1-35,在⊙0中,AB=CD,下列结论:
①AB=CD;
B
②AC=BD;
A
3∠AOC=∠BOD:
④AC=BD.
图24-1-35
其中正确的个数是
(
A.1个
B.2个
C.3个
D.4个
3.如图24-1-36,P为直径AB上一点,EF、CD为
过点P的两条弦,且∠DPB=∠EPB.求证:
(1CD=EF;
(2)CE =DF.
E
C
A
0
B
F
D
图24-1-36
E
C
M
A
B
N
F
D
1.下列说法正确的是
A.等弦所对的弧相等
B.等弧对的弦相等
C.圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
3.如图24-1-42,过△ABC的三个顶点作圆,将
△ABC绕圆心O逆时针方向旋转°(0<α<
90),得到△A'B'C'.若AB'=A'C=CB,则∠B的
度数为
(
A.30°
B.45
C.50°
D.60°
同课章节目录
