13.3.1等腰三角形的性质课件(第一课时)
文档属性
| 名称 | 13.3.1等腰三角形的性质课件(第一课时) |  | |
| 格式 | zip | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-27 16:47:29 | ||
图片预览





文档简介
课件21张PPT。13.3.1等腰三角形的性质 第一课时学习目标:
1.理解并掌握等腰三角形的性质,
2.能利用等腰三角形的性质证明线段或角的相等关系.
学习重点:
等腰三角形的性质及其应用.
学习难点:
等腰三角形三线合一的性质的理解及其应用.
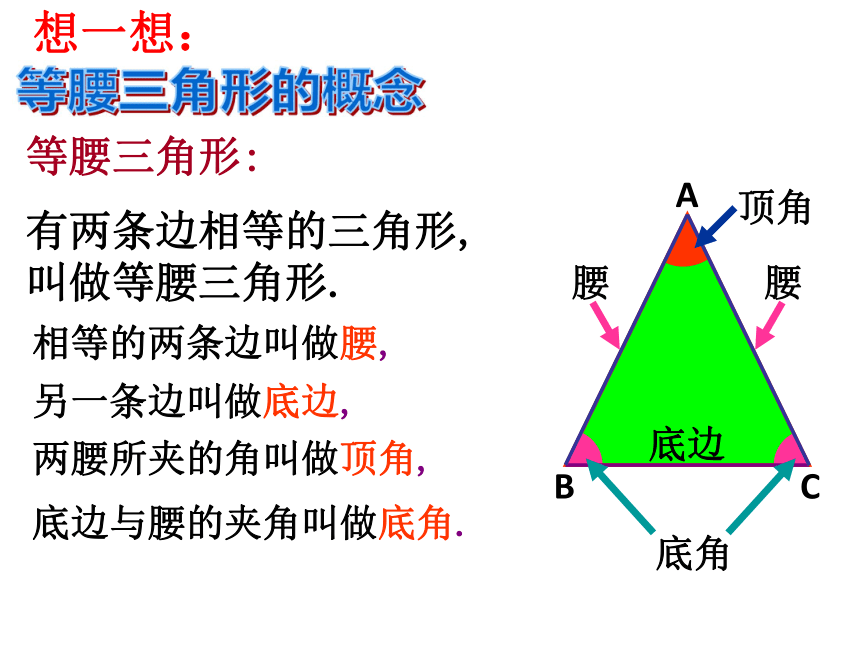
ABC等腰三角形:有两条边相等的三角形,
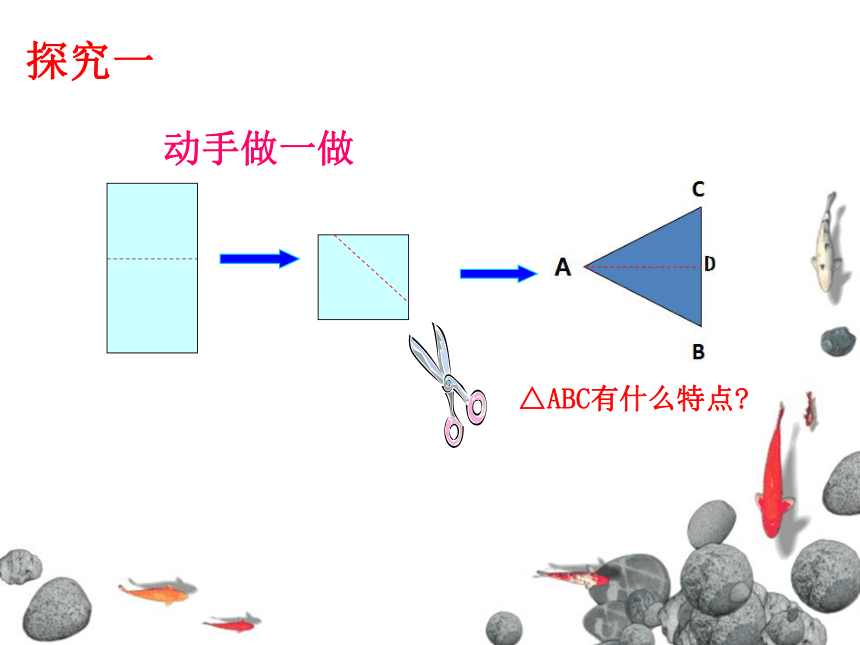
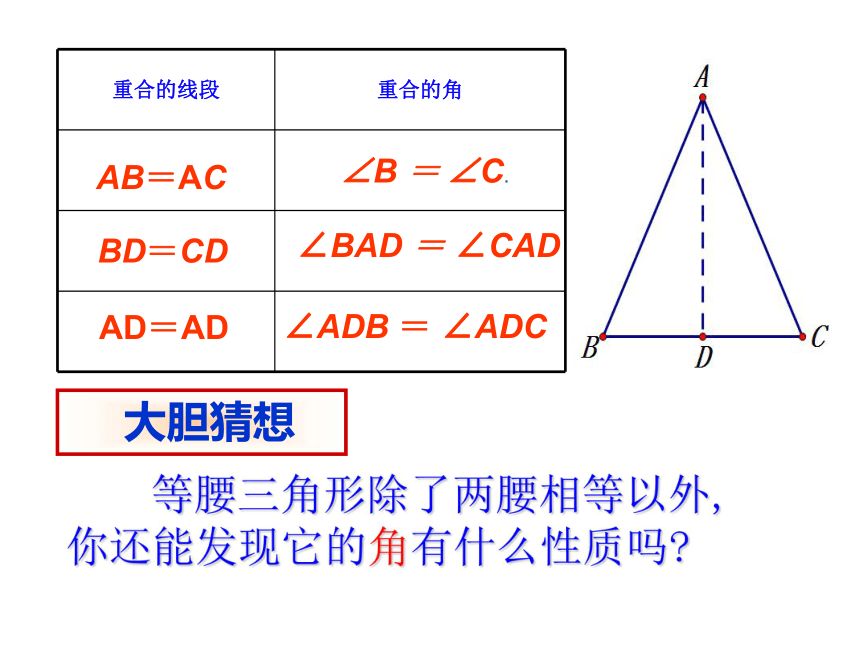
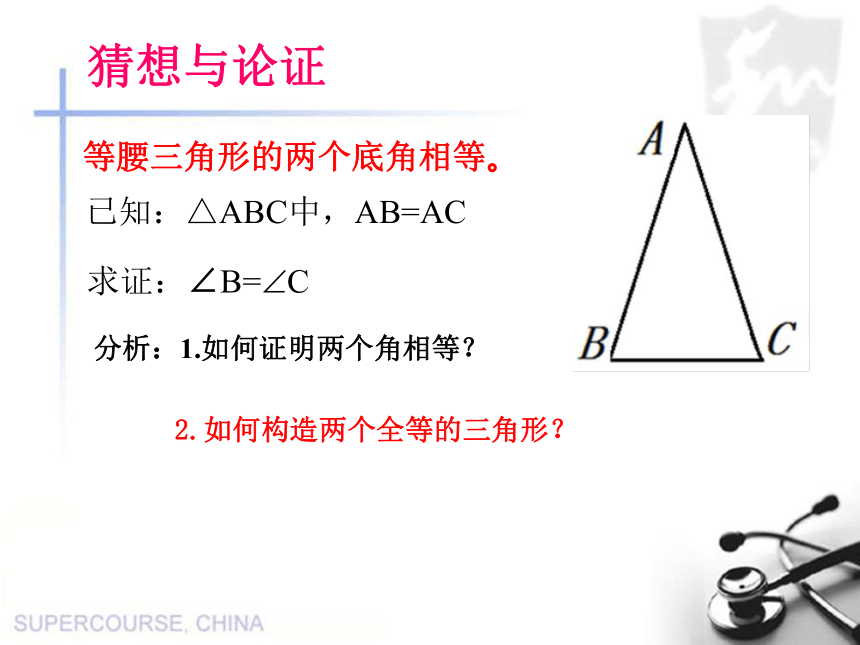
叫做等腰三角形.等腰三角形的概念相等的两条边叫做腰,另一条边叫做底边,底边与腰的夹角叫做底角.两腰所夹的角叫做顶角,腰腰底边顶角底角想一想:动手做一做△ABC有什么特点?探究一 AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD∠ADB = ∠ADC 等腰三角形除了两腰相等以外, 你还能发现它的角有什么性质吗? 大胆猜想猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形?已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作底边的中线AD,则BD=CDAB=AC ( 已知 )BD=CD ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).在△BAD和△CAD中方法一:作底边上的中线已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作顶角的平分线AD,则∠1=∠2AB=AC ( 已知 )∠1=∠2 ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).方法二:作顶角的平分线在△BAD和△CAD中12已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作底边的高线AD,则∠BDA=∠CDA=90°AB=AC ( 已知 )AD=AD (公共边) ∴ Rt△BAD ≌ Rt△CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).方法三:作底边的高线在Rt△BAD和Rt△CAD中用符号语言表示为:在△ABC中,
∵ AC=AB( 已知)
∴ ∠B=∠C (等边对等角)等腰三角形的两个底角相等等腰三角形的性质1:得出结论:(等边对等角)⒈等腰三角形一个底角为75°,它的另外两个角为:75°, 30°70°,40°或55°,55°35°,35°小试牛刀⒉等腰三角形一个角为70°,它的另外两个角为:3.等腰三角形一个角为110°,它的另外两个角为:① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°
⑤0°<底角<90°结论:在等腰三角形中,探究二: 刚才的证明除了能得到∠B=∠C 你还能发现什么?
AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD ∠ADB =∠ADC=90°(等腰三角形三线合一)性质2 等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合.小组讨论 性质3 等腰三角形是轴对称图形,其顶角的平分线(底边上的中线、底边上的高)所在的直线就是等腰三角形的对称轴。 1. 根据等腰三角形性质2填空,
在△ABC中, AB=AC, (1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD 知一线得二线
“三线合一”可以帮助我
们解决线段的垂直、相等
以及角的相等问题。小试牛刀 例1、如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。1、图中有哪几个等腰三角形?ABCD应用新知,体验成功。△ABC △ABD △BDC2、有哪些相等的角?∠ABC=∠ACB=∠BDC ∠ A=∠ABD3、这两组相等的角之间还有什么关系?∠BDC=2∠ A
∠ABC+∠ACB+∠ A=180 °例1、如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。xx2x2x2x解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,
有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,ABC=∠C=72°1、等腰三角形的顶角一定是锐角。
2、等腰三角形的底角可能是锐角或者直角、
钝角都可以。
3、等腰三角形的顶角平分线一定垂直底边。
4、等腰三角形的角平分线、中线和高互相重
合。
5、等腰三角形底边上的中线一定平分顶角(X)(X)(√)(X)(√)明辨是非 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
应用新知,体验成功。 如图:△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE。 求证:AH=2BD
证明:∵AB=AC,AD是高(已知)∴BC=2BD(三线合一)又∵BE是高(已知)∴∠ADC=∠BEC=∠AEH=90°(垂直的定义)在△AEH和△BEC中∴△AEH≌△BEC(ASA)∴∠1+∠C=∠2+∠C=90°∴ ∠1=∠2(同角的余角相等) ∴AH=BC(全等三角形的性质)∴AH=2BD(等量代换)摩拳擦掌 轴对称图形两个底角相等,简称“等边对等角”顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合 一”等腰三角形学习的数学思想及方法:
分类讨论和一题多解。解决等腰三角形问题时常用的辅助线谈谈你的收获!再见
1.理解并掌握等腰三角形的性质,
2.能利用等腰三角形的性质证明线段或角的相等关系.
学习重点:
等腰三角形的性质及其应用.
学习难点:
等腰三角形三线合一的性质的理解及其应用.
ABC等腰三角形:有两条边相等的三角形,
叫做等腰三角形.等腰三角形的概念相等的两条边叫做腰,另一条边叫做底边,底边与腰的夹角叫做底角.两腰所夹的角叫做顶角,腰腰底边顶角底角想一想:动手做一做△ABC有什么特点?探究一 AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD∠ADB = ∠ADC 等腰三角形除了两腰相等以外, 你还能发现它的角有什么性质吗? 大胆猜想猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=?C分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形?已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作底边的中线AD,则BD=CDAB=AC ( 已知 )BD=CD ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).在△BAD和△CAD中方法一:作底边上的中线已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作顶角的平分线AD,则∠1=∠2AB=AC ( 已知 )∠1=∠2 ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).方法二:作顶角的平分线在△BAD和△CAD中12已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.等腰三角形的两个底角相等。D证明: 作底边的高线AD,则∠BDA=∠CDA=90°AB=AC ( 已知 )AD=AD (公共边) ∴ Rt△BAD ≌ Rt△CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).方法三:作底边的高线在Rt△BAD和Rt△CAD中用符号语言表示为:在△ABC中,
∵ AC=AB( 已知)
∴ ∠B=∠C (等边对等角)等腰三角形的两个底角相等等腰三角形的性质1:得出结论:(等边对等角)⒈等腰三角形一个底角为75°,它的另外两个角为:75°, 30°70°,40°或55°,55°35°,35°小试牛刀⒉等腰三角形一个角为70°,它的另外两个角为:3.等腰三角形一个角为110°,它的另外两个角为:① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°
⑤0°<底角<90°结论:在等腰三角形中,探究二: 刚才的证明除了能得到∠B=∠C 你还能发现什么?
AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD ∠ADB =∠ADC=90°(等腰三角形三线合一)性质2 等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合.小组讨论 性质3 等腰三角形是轴对称图形,其顶角的平分线(底边上的中线、底边上的高)所在的直线就是等腰三角形的对称轴。 1. 根据等腰三角形性质2填空,
在△ABC中, AB=AC, (1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD 知一线得二线
“三线合一”可以帮助我
们解决线段的垂直、相等
以及角的相等问题。小试牛刀 例1、如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。1、图中有哪几个等腰三角形?ABCD应用新知,体验成功。△ABC △ABD △BDC2、有哪些相等的角?∠ABC=∠ACB=∠BDC ∠ A=∠ABD3、这两组相等的角之间还有什么关系?∠BDC=2∠ A
∠ABC+∠ACB+∠ A=180 °例1、如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。xx2x2x2x解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,
有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,ABC=∠C=72°1、等腰三角形的顶角一定是锐角。
2、等腰三角形的底角可能是锐角或者直角、
钝角都可以。
3、等腰三角形的顶角平分线一定垂直底边。
4、等腰三角形的角平分线、中线和高互相重
合。
5、等腰三角形底边上的中线一定平分顶角(X)(X)(√)(X)(√)明辨是非 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
应用新知,体验成功。 如图:△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE。 求证:AH=2BD
证明:∵AB=AC,AD是高(已知)∴BC=2BD(三线合一)又∵BE是高(已知)∴∠ADC=∠BEC=∠AEH=90°(垂直的定义)在△AEH和△BEC中∴△AEH≌△BEC(ASA)∴∠1+∠C=∠2+∠C=90°∴ ∠1=∠2(同角的余角相等) ∴AH=BC(全等三角形的性质)∴AH=2BD(等量代换)摩拳擦掌 轴对称图形两个底角相等,简称“等边对等角”顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合 一”等腰三角形学习的数学思想及方法:
分类讨论和一题多解。解决等腰三角形问题时常用的辅助线谈谈你的收获!再见
