11.3.1 多边形 课件(共31张PPT)
文档属性
| 名称 | 11.3.1 多边形 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 16:37:04 | ||
图片预览








文档简介
(共31张PPT)
11.3.1 多边形
人教版八年级上册
知识回顾
1.三角形内角和定理
三角形的内角和等于180°
2.直角三角形的性质、判定
直角三角形的两锐角互余;两锐角互余的三角形是直角三角形
3.三角形外角的性质
三角形的一个外角等于与它不相邻的两个内角和
4.三角形的外角和
三角形外角和等于180°
教学目标
1.了解并掌握多边形的定义及有关概念,能区分凸凹多边形.
2.理解正多边形及其有关概念.
3.掌握对角线条数与多边形的边数之间的关系.
新知导入
在前面的课程里我们学习、了解了三角形、四边形,在我们缤纷多彩的世界中,还有很多几何图形被用在生产、生活中,它们都在等待着我们去探索.......
我们来看看以下物体:
新知讲解
从生活用品到艺术品,从蜂巢到鸟巢,从现实到虚拟,多边形被大量的运用,今天我们就来学习多边形的相关内容。
多边形的定义
知识点 1
问题2:观察画某多边形的过程,类比三角形的概念,你能说出什么是多边形吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
问题1:回顾三角形的定义,什么是三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
新知探究
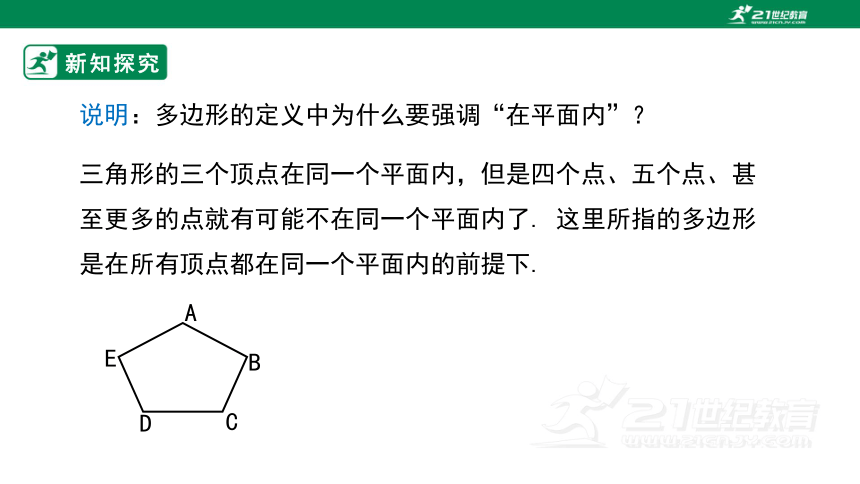
说明:多边形的定义中为什么要强调“在平面内”?
三角形的三个顶点在同一个平面内,但是四个点、五个点、甚至更多的点就有可能不在同一个平面内了. 这里所指的多边形是在所有顶点都在同一个平面内的前提下.
A
新知探究
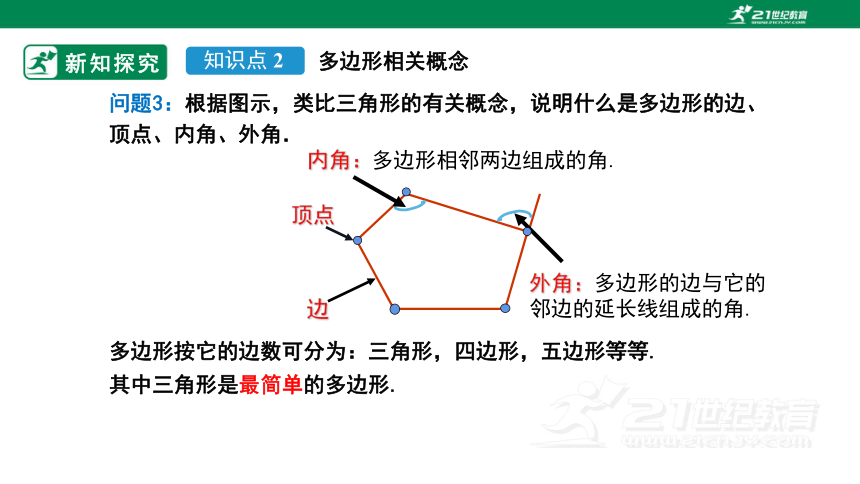
内角:多边形相邻两边组成的角.
问题3:根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
顶点
边
外角:多边形的边与它的邻边的延长线组成的角.
多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.
多边形相关概念
知识点 2
新知探究
多边形用图形名称以及它的各个顶点的大写字母表示,字母按照顶点的顺序书写,可以顺时针也可以逆时针.
例如:五边形ABCDE.
多边形的表示方法
A
新知探究
问4:三角形有3个顶点,3条边,3个内角、6个外角;四边形有4个顶点,4条边,4个内角、8个外角;
那么n边形有多少个顶点?多少条边?多少个内角?多少个外角?
归纳:1.多边形按照边数可以分为:三角形、四边形、五边形等,其中三角形是最简单的多边形.
2.n边形有n个顶点、n条边、n个内角、2n个外角.
新知探究
A
B
C
D
E
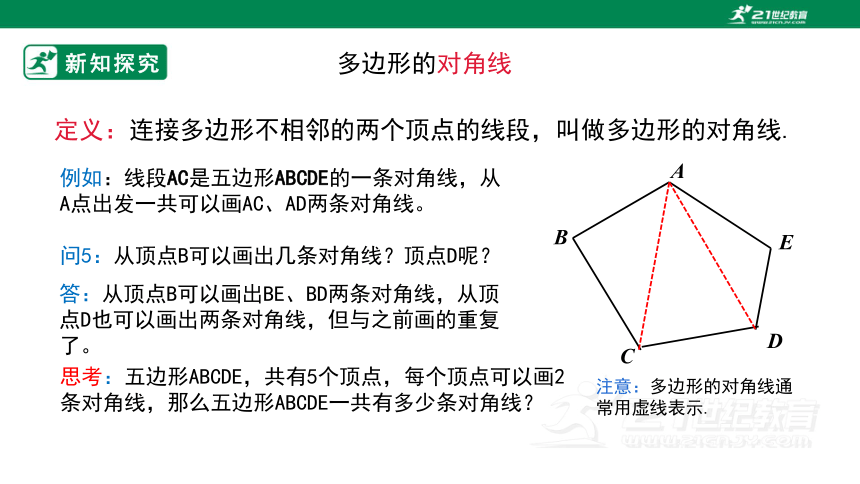
定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
多边形的对角线
例如:线段AC是五边形ABCDE的一条对角线,从A点出发一共可以画AC、AD两条对角线。
注意:多边形的对角线通常用虚线表示.
问5:从顶点B可以画出几条对角线?顶点D呢?
答:从顶点B可以画出BE、BD两条对角线,从顶点D也可以画出两条对角线,但与之前画的重复了。
思考:五边形ABCDE,共有5个顶点,每个顶点可以画2条对角线,那么五边形ABCDE一共有多少条对角线?
新知探究
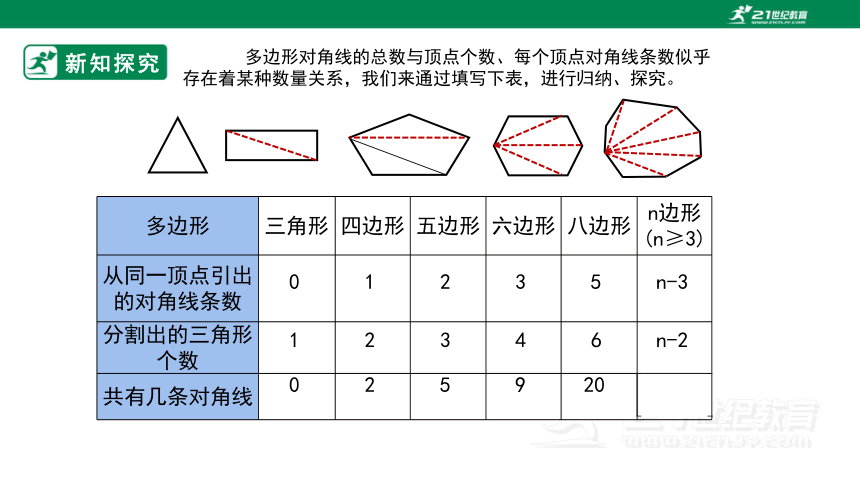
多边形 三角形 四边形 五边形 六边形 八边形 n边形(n≥3)
从同一顶点引出的对角线条数
分割出的三角形个数
共有几条对角线
0
1
0
1
2
2
2
3
5
3
4
9
5
6
20
n-3
n-2
多边形对角线的总数与顶点个数、每个顶点对角线条数似乎存在着某种数量关系,我们来通过填写下表,进行归纳、探究。
新知探究
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
归纳总结
新知典例
例1 过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为23,求这个多边形的边数.
解:设这个多边形为n边形,则有(n-3)条对角线,所分得的三角形个数为n-2,
∴n-3+n-2=23,
解得n=14.
答:该多边形的边数有14条.
课堂练习
1.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
C
2.一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
D
课堂练习
3. 若过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有k条对角线,正h边形的内角和与外角和相等.则代数式h (m﹣k)n的值为 。
解:∵n边形从一个顶点发出的对角线有n﹣3条,
∴m=7+3=10,n=3,k=5,h=4;
则 h (m﹣k)n=60.
60
新知探究
凸多边形
知识点 3
探究:比较下图两个多边形的区别.
A
D
C
B
A
C
B
D
①
②
画出CD所在的直线,发现①中的图形在这条直线的同一侧,而②中的图形不在这条直线的同一侧.
新知探究
定义:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 反之,称为凹多边形,本节只讨论凸多边形.
凸多边形
A
D
C
B
A
C
B
D
①
②
凹多边形
新知典例
例2 凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,
∴新多边形的边数为7、5、6三种情况,
如图所示.
探究小结
一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条.
①从所截角的两边裁,边数增加1.
②从所截角的相邻两角的顶点裁,边数减少1.
③从所截角的一边及相邻角的顶点裁,边数不变.
“裁角问题”的解法
分类
讨论
思想
新知练习
1.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7 C.5或6或7 D.6或7或8
解:如图可知,原来多边形的边数可能是5,6,7.
C
探究新知
正多边形的概念
知识点 4
问题6:在我们熟悉的三角形和四边形里,有一种特别的存在,那就是等边三角形和正方形。你能说说等边三角形和正方形特别的地方吗?
答:等边三角形三边相等、三个内角相等;正方形四边相等四个内角相等;
像等边三角形、正方形这样,各个角都相等,各条边都相等的多边形
叫做正多边形
正三角形
(等边三角形)
正方形
正五边形
正六边形
探究新知
问题7:下列图形是正多边形吗?如果不是,请说明为什么?
答:都不是.第一个不满足四个角相等,是菱形;
第二个不满足四边相等,是长方形.
若一个多边形是正多边形,则必须同时满足各边、各角都相等.
(四条边都相等)
(四个角都相等)
新知典例
例3 下列多边形中,不是凸多边形的是( )
A
B
C
D
B
例4 把一张形状是多边形的纸片剪去其中一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A. 六边形 B . 五边形 C.四边形 D.三角形
A
课堂练习
1.如图所示的图形中,属于多边形的有( )个.
A.3 B.4 C.5 D.6
A
课堂总结
多边形
定义
前提条件是在一个平面内
对角线
它是多边形的一条重要线段,在今后通常作对角线把多边形的问题转化为三角形和四边形的问题
正多
边形
定义既是判定也是性质
定义
用途
公式
连接多边形不相邻两个顶点的线段,叫做多边形的对角线
从一个顶点出发的对角线的总条数(n-3)条,多边形对角线的总条数
课堂练习
1.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
2.一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
C
D
课堂练习
3. 下列选项中的图形,不是凸多边形的是( )
A
B
C
D
A
4.若一个多边形截去一个角后,变成十六边形,那么原来的多边形的边数为( )
A.15或16或17 B.16或17
C.15或17 D.16或17或18
A
课堂练习
5.观察探究及应用.
(1)如图,观察图形并填空:
一个四边形有 条对角线;一个五边形有 条对角线;一个六边形有 条对角线;
(2)分析探究:
由凸n边形的一个顶点出发,可作 条对角线,多边形有n个顶点,若允许重复计数,共可作 条对角线;
(3)结论:一个凸n边形有 条对角线;
2
5
9
(n﹣3)
n(n﹣3)
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.3.1 多边形
人教版八年级上册
知识回顾
1.三角形内角和定理
三角形的内角和等于180°
2.直角三角形的性质、判定
直角三角形的两锐角互余;两锐角互余的三角形是直角三角形
3.三角形外角的性质
三角形的一个外角等于与它不相邻的两个内角和
4.三角形的外角和
三角形外角和等于180°
教学目标
1.了解并掌握多边形的定义及有关概念,能区分凸凹多边形.
2.理解正多边形及其有关概念.
3.掌握对角线条数与多边形的边数之间的关系.
新知导入
在前面的课程里我们学习、了解了三角形、四边形,在我们缤纷多彩的世界中,还有很多几何图形被用在生产、生活中,它们都在等待着我们去探索.......
我们来看看以下物体:
新知讲解
从生活用品到艺术品,从蜂巢到鸟巢,从现实到虚拟,多边形被大量的运用,今天我们就来学习多边形的相关内容。
多边形的定义
知识点 1
问题2:观察画某多边形的过程,类比三角形的概念,你能说出什么是多边形吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
问题1:回顾三角形的定义,什么是三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
新知探究
说明:多边形的定义中为什么要强调“在平面内”?
三角形的三个顶点在同一个平面内,但是四个点、五个点、甚至更多的点就有可能不在同一个平面内了. 这里所指的多边形是在所有顶点都在同一个平面内的前提下.
A
新知探究
内角:多边形相邻两边组成的角.
问题3:根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角.
顶点
边
外角:多边形的边与它的邻边的延长线组成的角.
多边形按它的边数可分为:三角形,四边形,五边形等等.其中三角形是最简单的多边形.
多边形相关概念
知识点 2
新知探究
多边形用图形名称以及它的各个顶点的大写字母表示,字母按照顶点的顺序书写,可以顺时针也可以逆时针.
例如:五边形ABCDE.
多边形的表示方法
A
新知探究
问4:三角形有3个顶点,3条边,3个内角、6个外角;四边形有4个顶点,4条边,4个内角、8个外角;
那么n边形有多少个顶点?多少条边?多少个内角?多少个外角?
归纳:1.多边形按照边数可以分为:三角形、四边形、五边形等,其中三角形是最简单的多边形.
2.n边形有n个顶点、n条边、n个内角、2n个外角.
新知探究
A
B
C
D
E
定义:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
多边形的对角线
例如:线段AC是五边形ABCDE的一条对角线,从A点出发一共可以画AC、AD两条对角线。
注意:多边形的对角线通常用虚线表示.
问5:从顶点B可以画出几条对角线?顶点D呢?
答:从顶点B可以画出BE、BD两条对角线,从顶点D也可以画出两条对角线,但与之前画的重复了。
思考:五边形ABCDE,共有5个顶点,每个顶点可以画2条对角线,那么五边形ABCDE一共有多少条对角线?
新知探究
多边形 三角形 四边形 五边形 六边形 八边形 n边形(n≥3)
从同一顶点引出的对角线条数
分割出的三角形个数
共有几条对角线
0
1
0
1
2
2
2
3
5
3
4
9
5
6
20
n-3
n-2
多边形对角线的总数与顶点个数、每个顶点对角线条数似乎存在着某种数量关系,我们来通过填写下表,进行归纳、探究。
新知探究
从n(n≥3)边形的一个顶点可以作出(n-3)条对角线.将多边形分成(n-2)个三角形.
n(n≥3)边形共有对角线 条.
归纳总结
新知典例
例1 过多边形的一个顶点的所有对角线的条数与这些对角线分该多边形所得三角形的个数的和为23,求这个多边形的边数.
解:设这个多边形为n边形,则有(n-3)条对角线,所分得的三角形个数为n-2,
∴n-3+n-2=23,
解得n=14.
答:该多边形的边数有14条.
课堂练习
1.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
C
2.一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
D
课堂练习
3. 若过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有k条对角线,正h边形的内角和与外角和相等.则代数式h (m﹣k)n的值为 。
解:∵n边形从一个顶点发出的对角线有n﹣3条,
∴m=7+3=10,n=3,k=5,h=4;
则 h (m﹣k)n=60.
60
新知探究
凸多边形
知识点 3
探究:比较下图两个多边形的区别.
A
D
C
B
A
C
B
D
①
②
画出CD所在的直线,发现①中的图形在这条直线的同一侧,而②中的图形不在这条直线的同一侧.
新知探究
定义:画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形. 反之,称为凹多边形,本节只讨论凸多边形.
凸多边形
A
D
C
B
A
C
B
D
①
②
凹多边形
新知典例
例2 凸六边形纸片剪去一个角后,得到的多边形的边数可能是多少?画出图形说明.
解:∵六边形截去一个角的边数有增加1、减少1、不变三种情况,
∴新多边形的边数为7、5、6三种情况,
如图所示.
探究小结
一个多边形截去一个角后,多边形的边数可能增加了一条,也可能不变或减少了一条.
①从所截角的两边裁,边数增加1.
②从所截角的相邻两角的顶点裁,边数减少1.
③从所截角的一边及相邻角的顶点裁,边数不变.
“裁角问题”的解法
分类
讨论
思想
新知练习
1.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7 C.5或6或7 D.6或7或8
解:如图可知,原来多边形的边数可能是5,6,7.
C
探究新知
正多边形的概念
知识点 4
问题6:在我们熟悉的三角形和四边形里,有一种特别的存在,那就是等边三角形和正方形。你能说说等边三角形和正方形特别的地方吗?
答:等边三角形三边相等、三个内角相等;正方形四边相等四个内角相等;
像等边三角形、正方形这样,各个角都相等,各条边都相等的多边形
叫做正多边形
正三角形
(等边三角形)
正方形
正五边形
正六边形
探究新知
问题7:下列图形是正多边形吗?如果不是,请说明为什么?
答:都不是.第一个不满足四个角相等,是菱形;
第二个不满足四边相等,是长方形.
若一个多边形是正多边形,则必须同时满足各边、各角都相等.
(四条边都相等)
(四个角都相等)
新知典例
例3 下列多边形中,不是凸多边形的是( )
A
B
C
D
B
例4 把一张形状是多边形的纸片剪去其中一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是( )
A. 六边形 B . 五边形 C.四边形 D.三角形
A
课堂练习
1.如图所示的图形中,属于多边形的有( )个.
A.3 B.4 C.5 D.6
A
课堂总结
多边形
定义
前提条件是在一个平面内
对角线
它是多边形的一条重要线段,在今后通常作对角线把多边形的问题转化为三角形和四边形的问题
正多
边形
定义既是判定也是性质
定义
用途
公式
连接多边形不相邻两个顶点的线段,叫做多边形的对角线
从一个顶点出发的对角线的总条数(n-3)条,多边形对角线的总条数
课堂练习
1.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
2.一个多边形从一个顶点最多能引出三条对角线,这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
C
D
课堂练习
3. 下列选项中的图形,不是凸多边形的是( )
A
B
C
D
A
4.若一个多边形截去一个角后,变成十六边形,那么原来的多边形的边数为( )
A.15或16或17 B.16或17
C.15或17 D.16或17或18
A
课堂练习
5.观察探究及应用.
(1)如图,观察图形并填空:
一个四边形有 条对角线;一个五边形有 条对角线;一个六边形有 条对角线;
(2)分析探究:
由凸n边形的一个顶点出发,可作 条对角线,多边形有n个顶点,若允许重复计数,共可作 条对角线;
(3)结论:一个凸n边形有 条对角线;
2
5
9
(n﹣3)
n(n﹣3)
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
