一次函数的图像和性质
图片预览



文档简介
课件12张PPT。12.2一次函数(3)-----一次函数的图像和性质 1.一次函数的一般形式
y=kx+b (k,b是常数,k≠0)
正比例函数的一般形式
y=kx (k是常数,k≠0)
二者有什么联系?
正比例函数是一次函数b=0时的特殊情形
旧知复习 2.正比例函数的图象有以下特点:
(1)正比例函数的图象都经过点(______)
(2)作正比例函数y=kx图象时,一般描两点( ),( ).
(3)正比例函数y=kx有下列性质:
当k>0时,图象过第 ____、 ____象限和原点, y随x的增大
而_____,图象自左向右是____的;
当k<0时,图象过第____、___象限和原点, y随x的增大
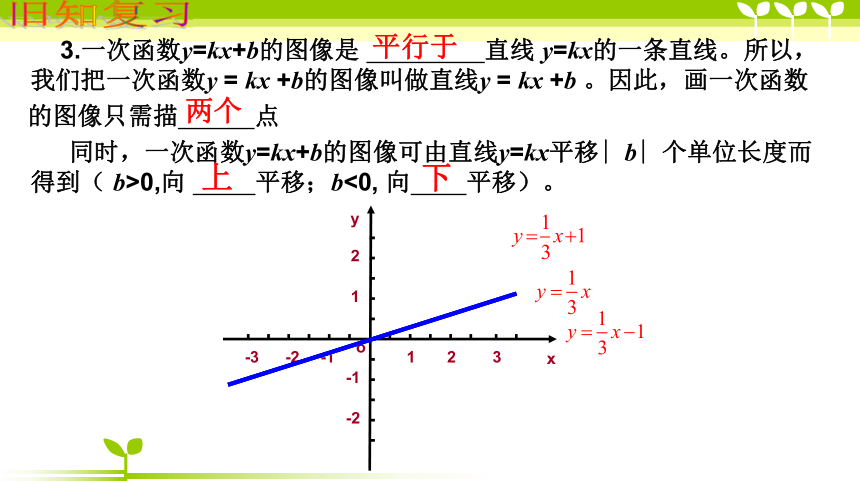
而_____,图象自左向右是______的.0 , 01,k0 , 0一三增大上升二四减小下降 3.一次函数y=kx+b的图像是 直线 y=kx的一条直线。所以,我们把一次函数y = kx +b的图像叫做直线y = kx +b 。因此,画一次函数
的图像只需描 点
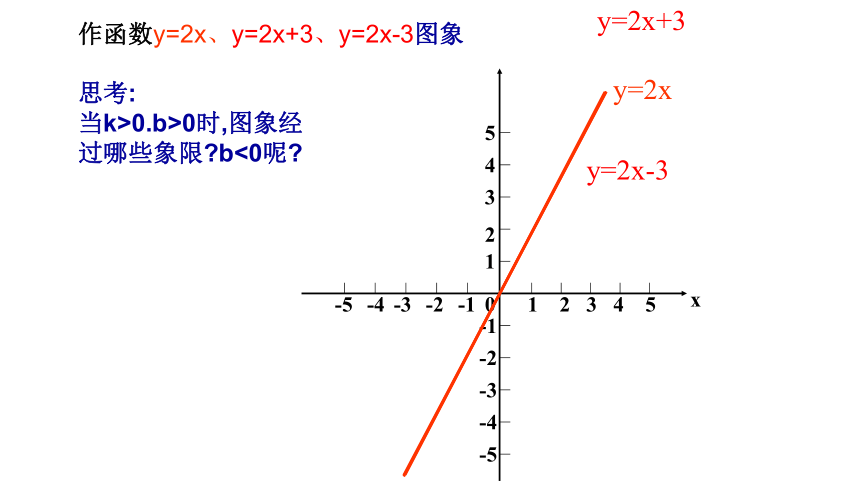
同时,一次函数y=kx+b的图像可由直线y=kx平移∣b∣个单位长度而得到( b>0,向 平移;b<0, 向 平移)。旧知复习平行于上下两个-3o-22123-1-1-2xy1y=2xy=2x+3y=2x-3作函数y=2x、y=2x+3、y=2x-3图象思考:
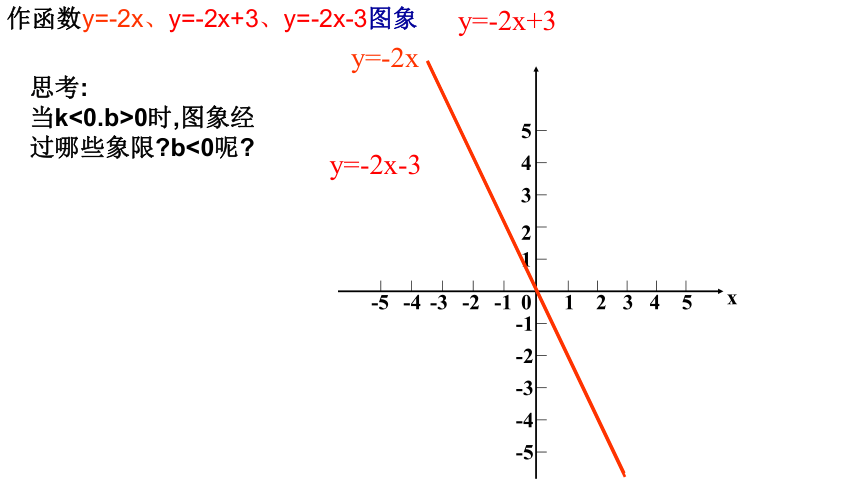
当k>0.b>0时,图象经过哪些象限?b<0呢?作函数y=-2x、y=-2x+3、y=-2x-3图象y=-2xy=-2x+3y=-2x-3思考:
当k<0.b>0时,图象经过哪些象限?b<0呢?观察分析: 当一个点在直线上从左向右移动时,它的位置怎样变化 自变量x由___到___函数y的值从___到___大小小大 当k>0 y随x的增大而增大,
这时函数的图象从左到右上升。 y=kx+b(k>0) 思考:当k<0时呢?b=0即y=kxb>0b<0b=0b>0b<0一次函数 y=kx+b中,k,b的取值跟图像的关系如下:一、三一、二、三一、三、四二、四一、二、四 二、三、四当k >0时,y的值随x的增大而增大当k <0时,y的值随x的增大而减小归纳:y=kx+b (k>0)y=kx+b (k<0)(0,b)(0,b)(0,b)(0,b)反馈检测
1、填空:
(1)对于y=7x,y随x的________而增大.
(2)对于y=-2x+3,y随x的增大而___________.
(3)已知一次函数y=(2m+1)x+5,若y随x的增大而增大,则m的取值范
围是______
2、直线y=-2x+3经过A(x1,y1)、B(x2,y2),当x1>x2时,y1与y2哪个大?
3、m取何值时,一次函数y=(m-1)x+m2-1的图象经过原点?
4、当b>0时,y=x+b的图象经过哪几个象限?当b<0时呢?增大减小m=-1一、二、三一、三、四y1(1)当m______时,y随x的增大而减小;
(2)当m______,n______时,函数图象与y轴的交点在x轴的下方;
(3)当m______,n______时,函数图象过原点.,它们在同一直角坐标系中大致5、两个一次函数的图象是( )6.拓展:已知一次函数y0xxxxyyy000A. B. C. D.y2
y1y1y1y2
y2
y2
B<-2≠-2<4≠-2=4通过本节课的学习,你有哪些收获?
提示:可以从学习知识.学习方法等方面来总结
感悟与收获谢谢同学们的合作
y=kx+b (k,b是常数,k≠0)
正比例函数的一般形式
y=kx (k是常数,k≠0)
二者有什么联系?
正比例函数是一次函数b=0时的特殊情形
旧知复习 2.正比例函数的图象有以下特点:
(1)正比例函数的图象都经过点(______)
(2)作正比例函数y=kx图象时,一般描两点( ),( ).
(3)正比例函数y=kx有下列性质:
当k>0时,图象过第 ____、 ____象限和原点, y随x的增大
而_____,图象自左向右是____的;
当k<0时,图象过第____、___象限和原点, y随x的增大
而_____,图象自左向右是______的.0 , 01,k0 , 0一三增大上升二四减小下降 3.一次函数y=kx+b的图像是 直线 y=kx的一条直线。所以,我们把一次函数y = kx +b的图像叫做直线y = kx +b 。因此,画一次函数
的图像只需描 点
同时,一次函数y=kx+b的图像可由直线y=kx平移∣b∣个单位长度而得到( b>0,向 平移;b<0, 向 平移)。旧知复习平行于上下两个-3o-22123-1-1-2xy1y=2xy=2x+3y=2x-3作函数y=2x、y=2x+3、y=2x-3图象思考:
当k>0.b>0时,图象经过哪些象限?b<0呢?作函数y=-2x、y=-2x+3、y=-2x-3图象y=-2xy=-2x+3y=-2x-3思考:
当k<0.b>0时,图象经过哪些象限?b<0呢?观察分析: 当一个点在直线上从左向右移动时,它的位置怎样变化 自变量x由___到___函数y的值从___到___大小小大 当k>0 y随x的增大而增大,
这时函数的图象从左到右上升。 y=kx+b(k>0) 思考:当k<0时呢?b=0即y=kxb>0b<0b=0b>0b<0一次函数 y=kx+b中,k,b的取值跟图像的关系如下:一、三一、二、三一、三、四二、四一、二、四 二、三、四当k >0时,y的值随x的增大而增大当k <0时,y的值随x的增大而减小归纳:y=kx+b (k>0)y=kx+b (k<0)(0,b)(0,b)(0,b)(0,b)反馈检测
1、填空:
(1)对于y=7x,y随x的________而增大.
(2)对于y=-2x+3,y随x的增大而___________.
(3)已知一次函数y=(2m+1)x+5,若y随x的增大而增大,则m的取值范
围是______
2、直线y=-2x+3经过A(x1,y1)、B(x2,y2),当x1>x2时,y1与y2哪个大?
3、m取何值时,一次函数y=(m-1)x+m2-1的图象经过原点?
4、当b>0时,y=x+b的图象经过哪几个象限?当b<0时呢?增大减小m=-1一、二、三一、三、四y1(1)当m______时,y随x的增大而减小;
(2)当m______,n______时,函数图象与y轴的交点在x轴的下方;
(3)当m______,n______时,函数图象过原点.,它们在同一直角坐标系中大致5、两个一次函数的图象是( )6.拓展:已知一次函数y0xxxxyyy000A. B. C. D.y2
y1y1y1y2
y2
y2
B<-2≠-2<4≠-2=4通过本节课的学习,你有哪些收获?
提示:可以从学习知识.学习方法等方面来总结
感悟与收获谢谢同学们的合作
