华师大版数学八年级上册 12.3.2完全平方公式 课件(共20张PPT)
文档属性
| 名称 | 华师大版数学八年级上册 12.3.2完全平方公式 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
完全平方公式
温故互查:(二人小组完成)
1.复述平方差公式;
2.复述多项式乘以多项式的法则。
两数和(差)的平方
长子七中 胡 霞
学习目标:
1.能推导两数和(差)的平方公式;
2.了解两数和(差)的平方公式的几何背景;
3.能利用公式进行简单计算.
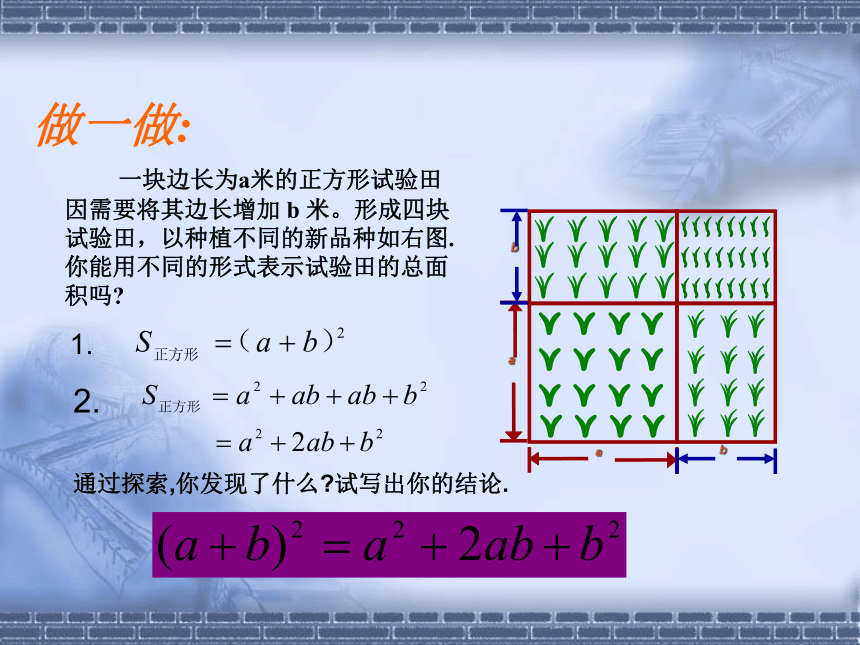
做一做:
一块边长为a米的正方形试验田因需要将其边长增加 b 米。形成四块试验田,以种植不同的新品种如右图.你能用不同的形式表示试验田的总面积吗
a
b
b
a
1.
2.
通过探索,你发现了什么 试写出你的结论.
想一想:
你能用多项式的乘法法则来说明它成立吗?
解:
两数和的平方公式:
符号语言:
文字语言: 两数和的平方,等于这两个数的平方和加上它们积的2倍.
几何背景:
先观察右图,再用等式表示下图中图形面积的运算:
a
b
a
b
ab
=
+
+
=
+
+
a
b
a
b
a
b
a
b
ab
2ab
认真阅读教材例4题,并仿照例题完成下列各题.
解:
1.
解:
解:
2.
3.
4.
解:
想一想:
如何计算 呢
(2)利用两数和的平方公式计算
解:
体现了“转化”的数学思想
(1)利用多项式的乘法法则计算;
解:
两数差的平方公式:
符号语言:
文字语言: 两数差的平方,等于这两数的平方和减去它们积的2倍.
几何背景:
ab
ab
=
—
+
=
—
+
观察右图,用等式表示下图中图形的面积公式:
a-b
b
a-b
b
a
a
2ab
认真阅读教材例5题,并仿照例题完成下列各题:
1.填空:
(m-1) = ( ) – 2 ( ) ( ) + ( )
(-s+t) = ( ) +2 ( ) ( )+ ( )
(-x-y) = ( ) + 2 ( ) ( ) + ( )
(-x-y) = ( ) - 2 ( ) ( ) + ( )
(-x-y) = [-( )] = ( )
2.计算:
m
1
1
m
-s
-s
t
t
-x
-x
-y
-y
-x
-x
y
y
解:
x+y
x+y
两数和(差)平方公式的结构特征:
左边是一个二次项的平方;
右边是一个二次三项式,其中有两项是左边二项式中每一项的平方,另一项是左边二项式中那两项的乘积的2倍.
口诀:首平方,尾平方,积的2倍放中央.
1、利用完全平方公式计算:
(1)(2x 3)2 ; (2) (4x+3y)2 ;
(3) ( m 0.4n)2; (4)
2、若(2a+1)2=(2a-1) 2 +( )成立, 则括号内的式子是( )
A.6a B.8a C.12a D.18a
3、下列等式成立的是 ( )
A.(a-b)2=a2-ab+b2 B.(a+3b )2=a2+9b2
C.(a+b)(a-b)=(b +a)(-b+ a) D. (x-9)(x+9)=x2-9
4、已知 是完全平方式,则 a 的值是( )
A、 B、-6 C、6 D、
自我检测:
B
C
D
解:
解:
解:
解:
知识盘点:
符号语言:
文字语言: 两数和的平方,等于这两个数的平方和加上它们积的2倍.
两数和的平方公式:
两数差的平方公式:
符号语言:
文字语言: 两数差的平方,等于这两数的平方和
减去它们积的2倍.
口诀: 首平方,尾平方,积的2倍放中央.
1.下列各式中,能够成立的等式是( ).
2. 若 是一个完全平方式,则m的值是___________
A、12 B、﹣12 C、±12 D、±6
3、运用完全平方公式计算:
(1) (2)
⑶ (4)( a-3b)(3b- a)
D
C
巩固训练:
A
B
C
D
拓展探究:
已知:a+b=10,ab=20,
求:(1) (2)
2.计算:
课堂小结
说说本节课的收获。
谢谢大家!
完全平方公式
温故互查:(二人小组完成)
1.复述平方差公式;
2.复述多项式乘以多项式的法则。
两数和(差)的平方
长子七中 胡 霞
学习目标:
1.能推导两数和(差)的平方公式;
2.了解两数和(差)的平方公式的几何背景;
3.能利用公式进行简单计算.
做一做:
一块边长为a米的正方形试验田因需要将其边长增加 b 米。形成四块试验田,以种植不同的新品种如右图.你能用不同的形式表示试验田的总面积吗
a
b
b
a
1.
2.
通过探索,你发现了什么 试写出你的结论.
想一想:
你能用多项式的乘法法则来说明它成立吗?
解:
两数和的平方公式:
符号语言:
文字语言: 两数和的平方,等于这两个数的平方和加上它们积的2倍.
几何背景:
先观察右图,再用等式表示下图中图形面积的运算:
a
b
a
b
ab
=
+
+
=
+
+
a
b
a
b
a
b
a
b
ab
2ab
认真阅读教材例4题,并仿照例题完成下列各题.
解:
1.
解:
解:
2.
3.
4.
解:
想一想:
如何计算 呢
(2)利用两数和的平方公式计算
解:
体现了“转化”的数学思想
(1)利用多项式的乘法法则计算;
解:
两数差的平方公式:
符号语言:
文字语言: 两数差的平方,等于这两数的平方和减去它们积的2倍.
几何背景:
ab
ab
=
—
+
=
—
+
观察右图,用等式表示下图中图形的面积公式:
a-b
b
a-b
b
a
a
2ab
认真阅读教材例5题,并仿照例题完成下列各题:
1.填空:
(m-1) = ( ) – 2 ( ) ( ) + ( )
(-s+t) = ( ) +2 ( ) ( )+ ( )
(-x-y) = ( ) + 2 ( ) ( ) + ( )
(-x-y) = ( ) - 2 ( ) ( ) + ( )
(-x-y) = [-( )] = ( )
2.计算:
m
1
1
m
-s
-s
t
t
-x
-x
-y
-y
-x
-x
y
y
解:
x+y
x+y
两数和(差)平方公式的结构特征:
左边是一个二次项的平方;
右边是一个二次三项式,其中有两项是左边二项式中每一项的平方,另一项是左边二项式中那两项的乘积的2倍.
口诀:首平方,尾平方,积的2倍放中央.
1、利用完全平方公式计算:
(1)(2x 3)2 ; (2) (4x+3y)2 ;
(3) ( m 0.4n)2; (4)
2、若(2a+1)2=(2a-1) 2 +( )成立, 则括号内的式子是( )
A.6a B.8a C.12a D.18a
3、下列等式成立的是 ( )
A.(a-b)2=a2-ab+b2 B.(a+3b )2=a2+9b2
C.(a+b)(a-b)=(b +a)(-b+ a) D. (x-9)(x+9)=x2-9
4、已知 是完全平方式,则 a 的值是( )
A、 B、-6 C、6 D、
自我检测:
B
C
D
解:
解:
解:
解:
知识盘点:
符号语言:
文字语言: 两数和的平方,等于这两个数的平方和加上它们积的2倍.
两数和的平方公式:
两数差的平方公式:
符号语言:
文字语言: 两数差的平方,等于这两数的平方和
减去它们积的2倍.
口诀: 首平方,尾平方,积的2倍放中央.
1.下列各式中,能够成立的等式是( ).
2. 若 是一个完全平方式,则m的值是___________
A、12 B、﹣12 C、±12 D、±6
3、运用完全平方公式计算:
(1) (2)
⑶ (4)( a-3b)(3b- a)
D
C
巩固训练:
A
B
C
D
拓展探究:
已知:a+b=10,ab=20,
求:(1) (2)
2.计算:
课堂小结
说说本节课的收获。
谢谢大家!
