人教版八年级数学上册11.1.2三角形的高、中线与角平分线同步练习(word、无答案)
文档属性
| 名称 | 人教版八年级数学上册11.1.2三角形的高、中线与角平分线同步练习(word、无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 90.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 16:31:43 | ||
图片预览

文档简介
11.1.2 三角形的高、中线与角平分线 同步精练
一.选择题
1.下列各组图形中,AD是△ABC的高的图形是( )
A.B.C.D.
2.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形B.面积相等的三角形 C.直角三角形D.周长相等的三角形
3.如图,AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm,则△ACD的周长为( )
A.19cm B.22cm C.25cm D.31cm
4.如图所示,△ABC中AC边上的高线是( )
A.线段DA B.线段BA C.线段BC D.线段BD
5.在三条边都不相等的三角形中,同一条边上的中线、高和这边所对角的角平分线,最短的是( )
A.高 B.中线 C.角平分线 D.不能确定
6.如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( )
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.
A.4个 B.3个 C.2个 D.1个
二.填空题
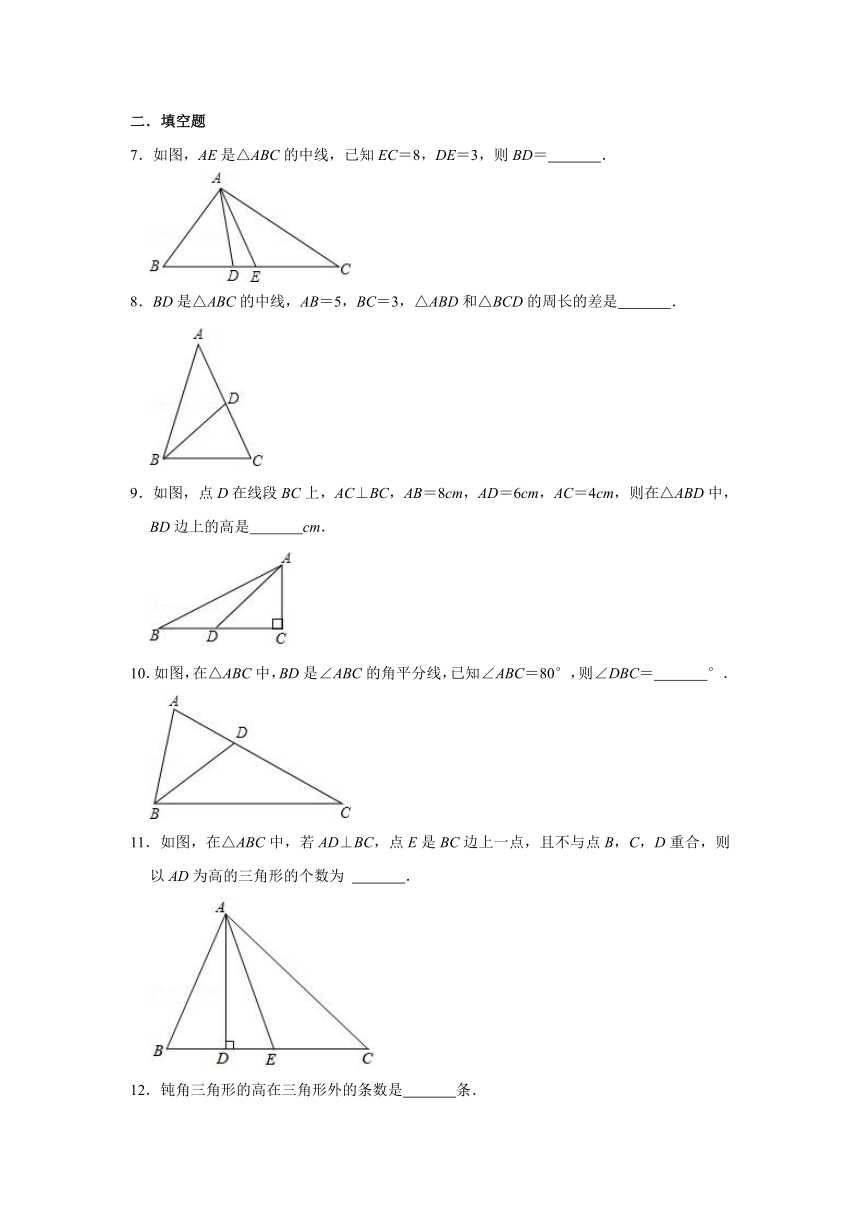
7.如图,AE是△ABC的中线,已知EC=8,DE=3,则BD= .
8.BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 .
9.如图,点D在线段BC上,AC⊥BC,AB=8cm,AD=6cm,AC=4cm,则在△ABD中,BD边上的高是 cm.
10.如图,在△ABC中,BD是∠ABC的角平分线,已知∠ABC=80°,则∠DBC= °.
11.如图,在△ABC中,若AD⊥BC,点E是BC边上一点,且不与点B,C,D重合,则以AD为高的三角形的个数为 .
12.钝角三角形的高在三角形外的条数是 条.
三.解答题
13.如图,已知△ABC和△EFD,在图中分别画出这两个三角形的三条高.
14.如图所示,AD是△ABC的中线,AE是△ACD的中线,已知DE=2cm,求BD,BE,BC的长.
15.如图,AD、AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系?
15.如图,在△ABC中,CD是中线,已知BC﹣AC=5cm,△DBC的周长为25cm,求△ADC的周长.
16.如图,在△ABC中,AD⊥BC,垂足为点D,EC⊥BC交AB于点E,CF⊥AB,垂足为点F,BG⊥AC,垂足为点G.
(1)分别写出△ABC各条边上的高;
(2)CF是哪几个三角形的高?
18.如图,武汉有三个车站A、B、C成三角形,一辆公共汽车从B站前往到C站.
(1)当汽车运动到点D点时,刚好BD=CD,连接线段AD,AD这条线段是什么线段?这样的线段在△ABC中有几条呢?此时有面积相等的三角形吗?
(2)汽车继续向前运动,当运动到点E时,发现∠BAE=∠CAE,那么AE这条线段是什么线段呢?在△ABC中,这样的线段又有几条呢?
(3)汽车继续向前运动,当运动到点F时,发现∠AFB=∠AFC=90°,则AF是什么线段?这样的线段在△ABC中有几条?
一.选择题
1.下列各组图形中,AD是△ABC的高的图形是( )
A.B.C.D.
2.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形B.面积相等的三角形 C.直角三角形D.周长相等的三角形
3.如图,AD是△ABC的中线,已知△ABD的周长为25cm,AB比AC长6cm,则△ACD的周长为( )
A.19cm B.22cm C.25cm D.31cm
4.如图所示,△ABC中AC边上的高线是( )
A.线段DA B.线段BA C.线段BC D.线段BD
5.在三条边都不相等的三角形中,同一条边上的中线、高和这边所对角的角平分线,最短的是( )
A.高 B.中线 C.角平分线 D.不能确定
6.如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( )
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.
A.4个 B.3个 C.2个 D.1个
二.填空题
7.如图,AE是△ABC的中线,已知EC=8,DE=3,则BD= .
8.BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 .
9.如图,点D在线段BC上,AC⊥BC,AB=8cm,AD=6cm,AC=4cm,则在△ABD中,BD边上的高是 cm.
10.如图,在△ABC中,BD是∠ABC的角平分线,已知∠ABC=80°,则∠DBC= °.
11.如图,在△ABC中,若AD⊥BC,点E是BC边上一点,且不与点B,C,D重合,则以AD为高的三角形的个数为 .
12.钝角三角形的高在三角形外的条数是 条.
三.解答题
13.如图,已知△ABC和△EFD,在图中分别画出这两个三角形的三条高.
14.如图所示,AD是△ABC的中线,AE是△ACD的中线,已知DE=2cm,求BD,BE,BC的长.
15.如图,AD、AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系?
15.如图,在△ABC中,CD是中线,已知BC﹣AC=5cm,△DBC的周长为25cm,求△ADC的周长.
16.如图,在△ABC中,AD⊥BC,垂足为点D,EC⊥BC交AB于点E,CF⊥AB,垂足为点F,BG⊥AC,垂足为点G.
(1)分别写出△ABC各条边上的高;
(2)CF是哪几个三角形的高?
18.如图,武汉有三个车站A、B、C成三角形,一辆公共汽车从B站前往到C站.
(1)当汽车运动到点D点时,刚好BD=CD,连接线段AD,AD这条线段是什么线段?这样的线段在△ABC中有几条呢?此时有面积相等的三角形吗?
(2)汽车继续向前运动,当运动到点E时,发现∠BAE=∠CAE,那么AE这条线段是什么线段呢?在△ABC中,这样的线段又有几条呢?
(3)汽车继续向前运动,当运动到点F时,发现∠AFB=∠AFC=90°,则AF是什么线段?这样的线段在△ABC中有几条?
