苏科版数学八年级上册 1.1~1.2:全等图形、全等三角形 阶段练习(原卷版+解析版)
文档属性
| 名称 | 苏科版数学八年级上册 1.1~1.2:全等图形、全等三角形 阶段练习(原卷版+解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 687.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 16:38:08 | ||
图片预览



文档简介
阶段练习1.1~1.2:全等图形、全等三角形
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·湖北省直辖县级单位·八年级期末)下列说法正确的是( )
A.两个面积相等的图形一定是全等图形 B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形 D.两个正三角形一定是全等图形
2、(2021·福建·福州三牧中学八年级期中)有下面的说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
3、(2021·重庆大足·八年级期末)如图,和全等,且,对应.若,,,则的长为( )
A.4 B.5 C.6 D.无法确定
(3题) (4题) (5)
4、(2022·云南昆明·三模)如图,,若,则的度数是( )
A.80° B.70° C.65° D.60°
5、(2022·陕西延安·八年级期末)如图,已知,,,则的长为( )
A.7 B.3.5 C.3 D.2
6、(2022·山东淄博·模拟预测)在中,,分别是,上的点,,则的度数( )
A.15 B.20 C.25 D.30
(6题) (7题) (8题)
7、(2022·河南驻马店·八年级期末)如图,,点和点是对应顶点,点和点是对应顶点,过点作,垂足为点,若,则的度数为( )
A. B. C. D.
8、如图,已知,下列结论:①;②;③;④;⑤;⑥;⑦.其中正确的有( )
A.4个 B.5个 C.6个 D.个
9、如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
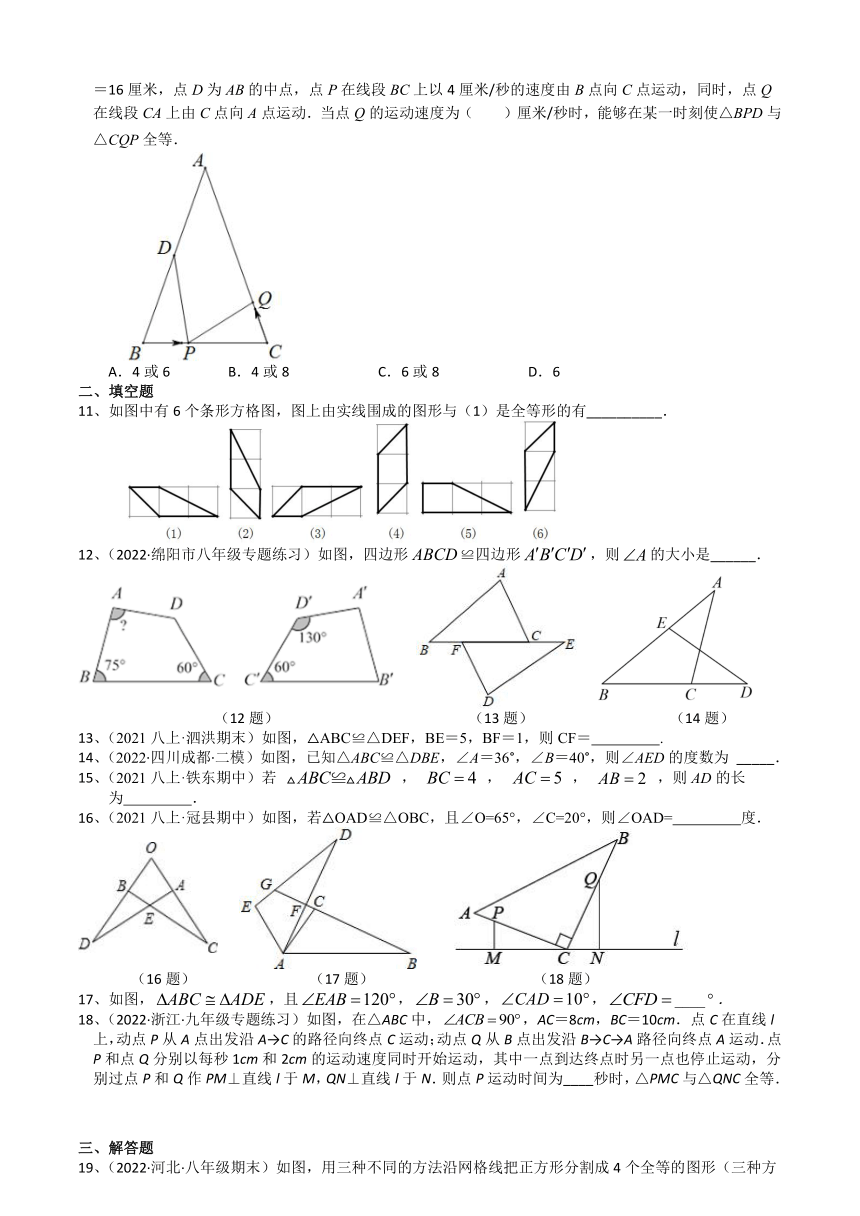
10、(2022·广西·南丹县教学研究室八年级期末)如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为( )厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
A.4或6 B.4或8 C.6或8 D.6
二、填空题
11、如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有__________.
12、(2022·绵阳市八年级专题练习)如图,四边形≌四边形,则的大小是______.
(12题) (13题) (14题)
13、(2021八上·泗洪期末)如图,△ABC≌△DEF,BE=5,BF=1,则CF= .
14、(2022·四川成都·二模)如图,已知△ABC≌△DBE,∠A=36°,∠B=40°,则∠AED的度数为 _____.
15、(2021八上·铁东期中)若 , , , ,则AD的长为 .
16、(2021八上·冠县期中)如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= 度.
(16题) (17题) (18题)
17、如图,,且,,,____.
18、(2022·浙江·九年级专题练习)如图,在△ABC中,,AC=8cm,BC=10cm.点C在直线l上,动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和2cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,分别过点P和Q作PM⊥直线l于M,QN⊥直线l于N.则点P运动时间为____秒时,△PMC与△QNC全等.
三、解答题
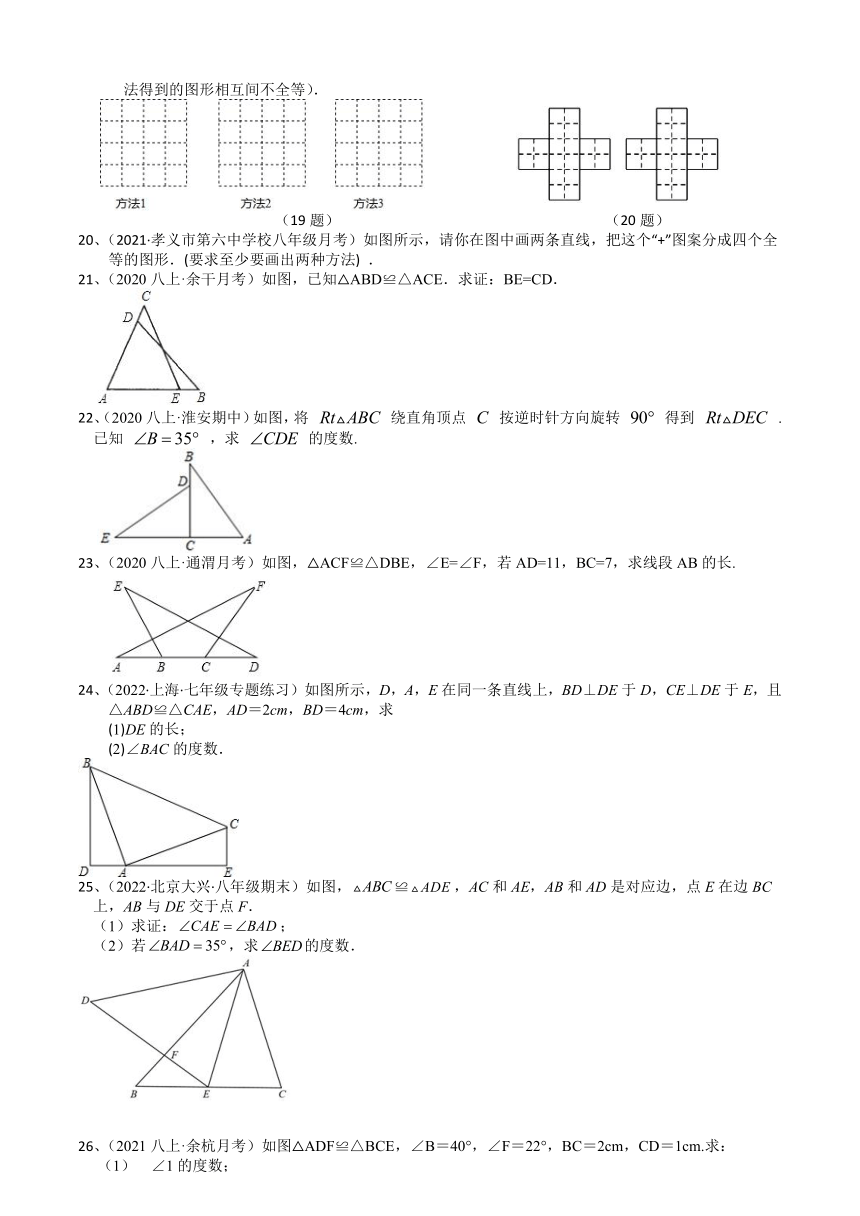
19、(2022·河北·八年级期末)如图,用三种不同的方法沿网格线把正方形分割成4个全等的图形(三种方法得到的图形相互间不全等).
(19题) (20题)
20、(2021·孝义市第六中学校八年级月考)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(要求至少要画出两种方法) .
21、(2020八上·余干月考)如图,已知△ABD≌△ACE.求证:BE=CD.
22、(2020八上·淮安期中)如图,将 绕直角顶点 按逆时针方向旋转 得到 .已知 ,求 的度数.
23、(2020八上·通渭月考)如图,△ACF≌△DBE,∠E=∠F,若AD=11,BC=7,求线段AB的长.
24、(2022·上海·七年级专题练习)如图所示,D,A,E在同一条直线上,BD⊥DE于D,CE⊥DE于E,且△ABD≌△CAE,AD=2cm,BD=4cm,求
(1)DE的长;
(2)∠BAC的度数.
25、(2022·北京大兴·八年级期末)如图,≌,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
26、(2021八上·余杭月考)如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求:
(1) ∠1的度数;
(2) AC的长.
27、(2022·安徽·安庆市石化第一中学八年级期末)如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.
(1)求AE的长度;
(2)求∠AED的度数.
28、(2021秋 灌云县月考)如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
29、(2021·江苏盐城·八年级期中)如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证∶ CE⊥AB
(2)已知BC=7,AD=5,求 AF的长.
阶段练习1.1~1.2:全等图形、全等三角形
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·湖北省直辖县级单位·八年级期末)下列说法正确的是( )
A.两个面积相等的图形一定是全等图形 B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形 D.两个正三角形一定是全等图形
【答案】B
解:A:两个面积相等的图形不一定是全等图形,故A错误,不符合题意;
B:两个全等图形形状一定相同,故B正确,符合题意;
C:两个周长相等的图形不一定是全等图形,故C错误,不符合题意;
D:两个正三角形不一定是全等图形,故D错误,不符合题意;
故选:B.
2、(2021·福建·福州三牧中学八年级期中)有下面的说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【详解】①全等三角形的形状相同,根据图形全等的定义,正确;
②全等三角形的对应边相等,根据全等三角形的性质,正确;
③全等三角形的对应角相等,根据全等三角形的性质,正确;
④全等三角形的周长、面积分别相等,正确;
故四个命题都正确, 故D为答案.
3、(2021·重庆大足·八年级期末)如图,和全等,且,对应.若,,,则的长为( )
A.4 B.5 C.6 D.无法确定
【答案】A
【详解】∵和全等,,对应
∴;∴AB=DF=4;故选:A.
4、(2022·云南昆明·三模)如图,,若,则的度数是( )
A.80° B.70° C.65° D.60°
【答案】B
【详解】,,
,,
,,故选:B.
5、(2022·陕西延安·八年级期末)如图,已知,,,则的长为( )
A.7 B.3.5 C.3 D.2
【答案】C
解:∵△ABC≌△DAE,∴AC=DE=5,AE=BC=2,∴CE=AC-AE=3, 故选C.
6、(2022·山东淄博·模拟预测)在中,,分别是,上的点,,则的度数( )
A.15 B.20 C.25 D.30
【答案】D
解:∵;∴,
,∴,∴,故选:.
7、(2022·河南驻马店·八年级期末)如图,,点和点是对应顶点,点和点是对应顶点,过点作,垂足为点,若,则的度数为( )
A. B. C. D.
解:∵,∴,
∴,即,
∵,∴,
∵,∴,∴;故选B.
8、如图,已知,下列结论:①;②;③;④;⑤;⑥;⑦.其中正确的有( )
A.4个 B.5个 C.6个 D.个
【答案】C
解:①∵;∴故①正确;
②∵;∴即:,故②正确;
③∵;∴;
∴即:,故③正确;
④∵;∴;∴,故④正确;
⑤∵;∴,故⑤正确;
⑥根据已知条件不能证得,故⑥错误;
⑦∵;∴;∴,故⑦正确;
故①②③④⑤⑦,正确的6个.故选C.
9、如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
【答案】C
解:如图延长C′D交AB′于H.
∵△AEB≌△AEB′,∴∠ABE=∠AB′E,
∵C′H∥EB′,∴∠AHC′=∠AB′E,∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=40°,∴∠C′AH=120°,
∴∠C′+∠AHC′=60°,∴∠BFC=60°+40°=100°, 故选:C.
10、(2022·广西·南丹县教学研究室八年级期末)如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为( )厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
A.4或6 B.4或8 C.6或8 D.6
解:设点Q的速度为x厘米/秒,则运动t秒时,CQ=xt,
∵P点的速度为4厘米/秒,BC=16厘米,∴BP=4t厘米,PC=(16-4t)厘米
又∵AB=AC=24厘米,点D为AB的中点;∴BD=AB=12厘米,
∵∠B=∠C,∴运动t秒时,△BPD与△CQP全等共有两种情况
①当△BPD≌△CQP时,则有BD=CP,BP=CQ;即12=16-4t,4t=xt;解得t=1,
∴由4t=xt可知,x=4.
②当△BPD≌△CPQ时,则有BD=CQ,BP=CP;即12=xt,4t=16-4t;∴t=2,x=6.
综合①②可知速度为4厘米/秒或6厘米/秒. 故选A.
二、填空题
11、如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有__________.
【答案】(2)(3)(6)
【详解】(6)以左下角顶点为定点逆时针旋转90°后,与(1)两个实线图形刚好重合,
(3)可上下反转成(1)的情况,与(1)两个实线图形刚好重合,
(2)以右下角顶点为定点顺时针旋转90°后成图(3),然后反转成(1)的情况,与(1)两个实线图形刚好重合,
(4)为平行四边形,而(1)为梯形,所以不能和(1)中图形完全重合,
(5)为直角梯形,而(1)不是,所以不能和(1)中图形完全重合,
故答案是:(2)(3)(6)
12、(2022·绵阳市八年级专题练习)如图,四边形≌四边形,则的大小是______.
【答案】
解:∵四边形≌四边形,
∴,∴;故答案为:95°.
13、(2021八上·泗洪期末)如图,△ABC≌△DEF,BE=5,BF=1,则CF= .
【答案】3
解:∵BE=5,BF=1,∴EF=BE﹣BF=4,
∵△ABC≌△DEF,∴BC=EF=4,∴CF=BC﹣BF=4-1=3.故答案为:3.
14、(2022·四川成都·二模)如图,已知△ABC≌△DBE,∠A=36°,∠B=40°,则∠AED的度数为 _____.
【答案】76°##76度
解:∵△ABC≌△DBE,∴∠A=∠D=36°,
∵∠AED是△BDE的外角,∴∠AED=∠B+∠D=40°+36°=76°.故答案为:76°.
15、(2021八上·铁东期中)若 , , , ,则AD的长为 .
【答案】5
解:∵△ABC≌△ABD,AC=5,∴AD=AC=5,故答案为:5.
16、(2021八上·冠县期中)如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= 度.
【答案】95
解:根据三角形内角和定理可得:∠OBC=180°-20°-65°=95°,
根据三角形全等的性质可得:∠OAD=∠OBC=95°.
17、如图,,且,,,____.
【答案】95
解:,,
,,,
, 故答案为:95.
18、(2022·浙江·九年级专题练习)如图,在△ABC中,,AC=8cm,BC=10cm.点C在直线l上,动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和2cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,分别过点P和Q作PM⊥直线l于M,QN⊥直线l于N.则点P运动时间为____秒时,△PMC与△QNC全等.
【答案】2或6
解:设运动时间为t秒时,△PMC≌△CNQ,∴斜边,
分两种情况:
①如图1,点P在AC上,点Q在BC上,
∵,,∴,,
∵,∴,∴;
图1 图2
②如图2,点P、Q都在AC上,此时点P、Q重合,
∵,,∴,∴;
综上所述,点P运动时间为2或6秒时,△PMC与△QNC全等, 故答案为:2或6.
三、解答题
19、(2022·河北·八年级期末)如图,用三种不同的方法沿网格线把正方形分割成4个全等的图形(三种方法得到的图形相互间不全等).
解:如图所示:
.
20、(2021·孝义市第六中学校八年级月考)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(要求至少要画出两种方法) .
解:如图所示:
21、(2020八上·余干月考)如图,已知△ABD≌△ACE.求证:BE=CD.
【答案】解:∵△ABD≌△ACE, ∴AD=AE,AB=AC,
∴BE=AB-AE=AC-AD=CD.
22、(2020八上·淮安期中)如图,将 绕直角顶点 按逆时针方向旋转 得到 .已知 ,求 的度数.
【答案】解:∵;∴
∵将 绕直角顶点 按逆时针方向旋转 得到
∴; ∴ .
23、(2020八上·通渭月考)如图,△ACF≌△DBE,∠E=∠F,若AD=11,BC=7,求线段AB的长.
【答案】解:∵△ACF≌△DBE,∴AC=DB, ∴AC–BC=DB–BC,即AB=CD,
∵AD=11,BC=7,∴AB= (AD–BC)= ×(11–7)=2,即AB=2.
24、(2022·上海·七年级专题练习)如图所示,D,A,E在同一条直线上,BD⊥DE于D,CE⊥DE于E,且△ABD≌△CAE,AD=2cm,BD=4cm,求(1)DE的长; (2)∠BAC的度数.
【答案】(1);(2)
解:(1)∵△ABD≌△CAE,AD=2cm,BD=4cm,
∴AE=BD=4cm,∴DE=AD+AE=6cm.
(2)∵BD⊥DE,∴∠D=90°,∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,∴∠DBA=∠CAE; ∴∠BAD+∠CAE=90°,∴∠BAC=90°.
25、(2022·北京大兴·八年级期末)如图,≌,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.(1)求证:;
(2)若,求的度数.
【详解】
(1)证明:∵≌,∴∠BAC=∠DAE,
即∠CAE+∠BAE=∠BAD+∠BAE,∴;
(2)∵,,∴∠CAE=35°,
∵≌,∴∠C=∠AED,
∵∠AEB=∠C+∠CAE,∠AEB=∠AED+∠BED,∴∠BED=∠CAE=35°.
26、(2021八上·余杭月考)如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求:
(1) ∠1的度数; (2) AC的长.
【答案】(1)解:∵;∴
由三角形外角的性质可得: ;∠1的度数为
(2)解:∵;∴
∴; 即AC的长为
27、(2022·安徽·安庆市石化第一中学八年级期末)如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.
(1)求AE的长度;
(2)求∠AED的度数.
【答案】(1);(2).
解:(1)∵,∴,∵,∴;
(2)∵,∴,
∵, ∴.
28、(2021秋 灌云县月考)如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
【解答】(1)证明:∵△ABC≌△DAE,∴AE=BC,AC=DE,
又∵AE=AC+CE,∴BC=DE+CE;
(2)解:∵BC∥DE,∴∠BCE=∠E,
又∵△ABC≌△DAE,∴∠ACB=∠E,∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
29、(2021·江苏盐城·八年级期中)如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证∶ CE⊥AB
(2)已知BC=7,AD=5,求 AF的长.
【详解】(1)证明:∵AD⊥BC∴∠CDF=90°
∵△ABD≌△CFD,∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,∴∠AEF=∠CDF=90°,∴CE⊥AB;
(2)解:∵△ABD≌△CFD,∴BD=DF,AD=DC,
∵BC=7,AD=5,∴BD=BC CD=2,∴AF=AD DF=5 2=3.
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·湖北省直辖县级单位·八年级期末)下列说法正确的是( )
A.两个面积相等的图形一定是全等图形 B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形 D.两个正三角形一定是全等图形
2、(2021·福建·福州三牧中学八年级期中)有下面的说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
3、(2021·重庆大足·八年级期末)如图,和全等,且,对应.若,,,则的长为( )
A.4 B.5 C.6 D.无法确定
(3题) (4题) (5)
4、(2022·云南昆明·三模)如图,,若,则的度数是( )
A.80° B.70° C.65° D.60°
5、(2022·陕西延安·八年级期末)如图,已知,,,则的长为( )
A.7 B.3.5 C.3 D.2
6、(2022·山东淄博·模拟预测)在中,,分别是,上的点,,则的度数( )
A.15 B.20 C.25 D.30
(6题) (7题) (8题)
7、(2022·河南驻马店·八年级期末)如图,,点和点是对应顶点,点和点是对应顶点,过点作,垂足为点,若,则的度数为( )
A. B. C. D.
8、如图,已知,下列结论:①;②;③;④;⑤;⑥;⑦.其中正确的有( )
A.4个 B.5个 C.6个 D.个
9、如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
10、(2022·广西·南丹县教学研究室八年级期末)如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为( )厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
A.4或6 B.4或8 C.6或8 D.6
二、填空题
11、如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有__________.
12、(2022·绵阳市八年级专题练习)如图,四边形≌四边形,则的大小是______.
(12题) (13题) (14题)
13、(2021八上·泗洪期末)如图,△ABC≌△DEF,BE=5,BF=1,则CF= .
14、(2022·四川成都·二模)如图,已知△ABC≌△DBE,∠A=36°,∠B=40°,则∠AED的度数为 _____.
15、(2021八上·铁东期中)若 , , , ,则AD的长为 .
16、(2021八上·冠县期中)如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= 度.
(16题) (17题) (18题)
17、如图,,且,,,____.
18、(2022·浙江·九年级专题练习)如图,在△ABC中,,AC=8cm,BC=10cm.点C在直线l上,动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和2cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,分别过点P和Q作PM⊥直线l于M,QN⊥直线l于N.则点P运动时间为____秒时,△PMC与△QNC全等.
三、解答题
19、(2022·河北·八年级期末)如图,用三种不同的方法沿网格线把正方形分割成4个全等的图形(三种方法得到的图形相互间不全等).
(19题) (20题)
20、(2021·孝义市第六中学校八年级月考)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(要求至少要画出两种方法) .
21、(2020八上·余干月考)如图,已知△ABD≌△ACE.求证:BE=CD.
22、(2020八上·淮安期中)如图,将 绕直角顶点 按逆时针方向旋转 得到 .已知 ,求 的度数.
23、(2020八上·通渭月考)如图,△ACF≌△DBE,∠E=∠F,若AD=11,BC=7,求线段AB的长.
24、(2022·上海·七年级专题练习)如图所示,D,A,E在同一条直线上,BD⊥DE于D,CE⊥DE于E,且△ABD≌△CAE,AD=2cm,BD=4cm,求
(1)DE的长;
(2)∠BAC的度数.
25、(2022·北京大兴·八年级期末)如图,≌,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.
(1)求证:;
(2)若,求的度数.
26、(2021八上·余杭月考)如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求:
(1) ∠1的度数;
(2) AC的长.
27、(2022·安徽·安庆市石化第一中学八年级期末)如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.
(1)求AE的长度;
(2)求∠AED的度数.
28、(2021秋 灌云县月考)如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
29、(2021·江苏盐城·八年级期中)如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证∶ CE⊥AB
(2)已知BC=7,AD=5,求 AF的长.
阶段练习1.1~1.2:全等图形、全等三角形
-2022-2023学年苏科版数学八年级上册
一、选择题
1、(2022·湖北省直辖县级单位·八年级期末)下列说法正确的是( )
A.两个面积相等的图形一定是全等图形 B.两个全等图形形状一定相同
C.两个周长相等的图形一定是全等图形 D.两个正三角形一定是全等图形
【答案】B
解:A:两个面积相等的图形不一定是全等图形,故A错误,不符合题意;
B:两个全等图形形状一定相同,故B正确,符合题意;
C:两个周长相等的图形不一定是全等图形,故C错误,不符合题意;
D:两个正三角形不一定是全等图形,故D错误,不符合题意;
故选:B.
2、(2021·福建·福州三牧中学八年级期中)有下面的说法:①全等三角形的形状相同;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【详解】①全等三角形的形状相同,根据图形全等的定义,正确;
②全等三角形的对应边相等,根据全等三角形的性质,正确;
③全等三角形的对应角相等,根据全等三角形的性质,正确;
④全等三角形的周长、面积分别相等,正确;
故四个命题都正确, 故D为答案.
3、(2021·重庆大足·八年级期末)如图,和全等,且,对应.若,,,则的长为( )
A.4 B.5 C.6 D.无法确定
【答案】A
【详解】∵和全等,,对应
∴;∴AB=DF=4;故选:A.
4、(2022·云南昆明·三模)如图,,若,则的度数是( )
A.80° B.70° C.65° D.60°
【答案】B
【详解】,,
,,
,,故选:B.
5、(2022·陕西延安·八年级期末)如图,已知,,,则的长为( )
A.7 B.3.5 C.3 D.2
【答案】C
解:∵△ABC≌△DAE,∴AC=DE=5,AE=BC=2,∴CE=AC-AE=3, 故选C.
6、(2022·山东淄博·模拟预测)在中,,分别是,上的点,,则的度数( )
A.15 B.20 C.25 D.30
【答案】D
解:∵;∴,
,∴,∴,故选:.
7、(2022·河南驻马店·八年级期末)如图,,点和点是对应顶点,点和点是对应顶点,过点作,垂足为点,若,则的度数为( )
A. B. C. D.
解:∵,∴,
∴,即,
∵,∴,
∵,∴,∴;故选B.
8、如图,已知,下列结论:①;②;③;④;⑤;⑥;⑦.其中正确的有( )
A.4个 B.5个 C.6个 D.个
【答案】C
解:①∵;∴故①正确;
②∵;∴即:,故②正确;
③∵;∴;
∴即:,故③正确;
④∵;∴;∴,故④正确;
⑤∵;∴,故⑤正确;
⑥根据已知条件不能证得,故⑥错误;
⑦∵;∴;∴,故⑦正确;
故①②③④⑤⑦,正确的6个.故选C.
9、如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且,BE、CD交于点F.若∠BAC=40°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
【答案】C
解:如图延长C′D交AB′于H.
∵△AEB≌△AEB′,∴∠ABE=∠AB′E,
∵C′H∥EB′,∴∠AHC′=∠AB′E,∴∠ABE=∠AHC′,
∵△ADC≌△ADC′,∴∠C′=∠ACD,
∵∠BFC=∠DBF+∠BDF,∠BDF=∠CAD+∠ACD,∴∠BFC=∠AHC′+∠C′+∠DAC,
∵∠DAC=∠DAC′=∠CAB′=40°,∴∠C′AH=120°,
∴∠C′+∠AHC′=60°,∴∠BFC=60°+40°=100°, 故选:C.
10、(2022·广西·南丹县教学研究室八年级期末)如图,在△ABC中,AB=AC=24厘米,∠B=∠C ,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为( )厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
A.4或6 B.4或8 C.6或8 D.6
解:设点Q的速度为x厘米/秒,则运动t秒时,CQ=xt,
∵P点的速度为4厘米/秒,BC=16厘米,∴BP=4t厘米,PC=(16-4t)厘米
又∵AB=AC=24厘米,点D为AB的中点;∴BD=AB=12厘米,
∵∠B=∠C,∴运动t秒时,△BPD与△CQP全等共有两种情况
①当△BPD≌△CQP时,则有BD=CP,BP=CQ;即12=16-4t,4t=xt;解得t=1,
∴由4t=xt可知,x=4.
②当△BPD≌△CPQ时,则有BD=CQ,BP=CP;即12=xt,4t=16-4t;∴t=2,x=6.
综合①②可知速度为4厘米/秒或6厘米/秒. 故选A.
二、填空题
11、如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有__________.
【答案】(2)(3)(6)
【详解】(6)以左下角顶点为定点逆时针旋转90°后,与(1)两个实线图形刚好重合,
(3)可上下反转成(1)的情况,与(1)两个实线图形刚好重合,
(2)以右下角顶点为定点顺时针旋转90°后成图(3),然后反转成(1)的情况,与(1)两个实线图形刚好重合,
(4)为平行四边形,而(1)为梯形,所以不能和(1)中图形完全重合,
(5)为直角梯形,而(1)不是,所以不能和(1)中图形完全重合,
故答案是:(2)(3)(6)
12、(2022·绵阳市八年级专题练习)如图,四边形≌四边形,则的大小是______.
【答案】
解:∵四边形≌四边形,
∴,∴;故答案为:95°.
13、(2021八上·泗洪期末)如图,△ABC≌△DEF,BE=5,BF=1,则CF= .
【答案】3
解:∵BE=5,BF=1,∴EF=BE﹣BF=4,
∵△ABC≌△DEF,∴BC=EF=4,∴CF=BC﹣BF=4-1=3.故答案为:3.
14、(2022·四川成都·二模)如图,已知△ABC≌△DBE,∠A=36°,∠B=40°,则∠AED的度数为 _____.
【答案】76°##76度
解:∵△ABC≌△DBE,∴∠A=∠D=36°,
∵∠AED是△BDE的外角,∴∠AED=∠B+∠D=40°+36°=76°.故答案为:76°.
15、(2021八上·铁东期中)若 , , , ,则AD的长为 .
【答案】5
解:∵△ABC≌△ABD,AC=5,∴AD=AC=5,故答案为:5.
16、(2021八上·冠县期中)如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= 度.
【答案】95
解:根据三角形内角和定理可得:∠OBC=180°-20°-65°=95°,
根据三角形全等的性质可得:∠OAD=∠OBC=95°.
17、如图,,且,,,____.
【答案】95
解:,,
,,,
, 故答案为:95.
18、(2022·浙江·九年级专题练习)如图,在△ABC中,,AC=8cm,BC=10cm.点C在直线l上,动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和2cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,分别过点P和Q作PM⊥直线l于M,QN⊥直线l于N.则点P运动时间为____秒时,△PMC与△QNC全等.
【答案】2或6
解:设运动时间为t秒时,△PMC≌△CNQ,∴斜边,
分两种情况:
①如图1,点P在AC上,点Q在BC上,
∵,,∴,,
∵,∴,∴;
图1 图2
②如图2,点P、Q都在AC上,此时点P、Q重合,
∵,,∴,∴;
综上所述,点P运动时间为2或6秒时,△PMC与△QNC全等, 故答案为:2或6.
三、解答题
19、(2022·河北·八年级期末)如图,用三种不同的方法沿网格线把正方形分割成4个全等的图形(三种方法得到的图形相互间不全等).
解:如图所示:
.
20、(2021·孝义市第六中学校八年级月考)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(要求至少要画出两种方法) .
解:如图所示:
21、(2020八上·余干月考)如图,已知△ABD≌△ACE.求证:BE=CD.
【答案】解:∵△ABD≌△ACE, ∴AD=AE,AB=AC,
∴BE=AB-AE=AC-AD=CD.
22、(2020八上·淮安期中)如图,将 绕直角顶点 按逆时针方向旋转 得到 .已知 ,求 的度数.
【答案】解:∵;∴
∵将 绕直角顶点 按逆时针方向旋转 得到
∴; ∴ .
23、(2020八上·通渭月考)如图,△ACF≌△DBE,∠E=∠F,若AD=11,BC=7,求线段AB的长.
【答案】解:∵△ACF≌△DBE,∴AC=DB, ∴AC–BC=DB–BC,即AB=CD,
∵AD=11,BC=7,∴AB= (AD–BC)= ×(11–7)=2,即AB=2.
24、(2022·上海·七年级专题练习)如图所示,D,A,E在同一条直线上,BD⊥DE于D,CE⊥DE于E,且△ABD≌△CAE,AD=2cm,BD=4cm,求(1)DE的长; (2)∠BAC的度数.
【答案】(1);(2)
解:(1)∵△ABD≌△CAE,AD=2cm,BD=4cm,
∴AE=BD=4cm,∴DE=AD+AE=6cm.
(2)∵BD⊥DE,∴∠D=90°,∴∠DBA+∠BAD=90°,
∵△ABD≌△CAE,∴∠DBA=∠CAE; ∴∠BAD+∠CAE=90°,∴∠BAC=90°.
25、(2022·北京大兴·八年级期末)如图,≌,AC和AE,AB和AD是对应边,点E在边BC上,AB与DE交于点F.(1)求证:;
(2)若,求的度数.
【详解】
(1)证明:∵≌,∴∠BAC=∠DAE,
即∠CAE+∠BAE=∠BAD+∠BAE,∴;
(2)∵,,∴∠CAE=35°,
∵≌,∴∠C=∠AED,
∵∠AEB=∠C+∠CAE,∠AEB=∠AED+∠BED,∴∠BED=∠CAE=35°.
26、(2021八上·余杭月考)如图△ADF≌△BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求:
(1) ∠1的度数; (2) AC的长.
【答案】(1)解:∵;∴
由三角形外角的性质可得: ;∠1的度数为
(2)解:∵;∴
∴; 即AC的长为
27、(2022·安徽·安庆市石化第一中学八年级期末)如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.
(1)求AE的长度;
(2)求∠AED的度数.
【答案】(1);(2).
解:(1)∵,∴,∵,∴;
(2)∵,∴,
∵, ∴.
28、(2021秋 灌云县月考)如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
【解答】(1)证明:∵△ABC≌△DAE,∴AE=BC,AC=DE,
又∵AE=AC+CE,∴BC=DE+CE;
(2)解:∵BC∥DE,∴∠BCE=∠E,
又∵△ABC≌△DAE,∴∠ACB=∠E,∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
29、(2021·江苏盐城·八年级期中)如图所示,已知△ABD≌△CFD,AD⊥BC于D.
(1)求证∶ CE⊥AB
(2)已知BC=7,AD=5,求 AF的长.
【详解】(1)证明:∵AD⊥BC∴∠CDF=90°
∵△ABD≌△CFD,∴∠BAD=∠DCF,
又∵∠AFE=∠CFD,∴∠AEF=∠CDF=90°,∴CE⊥AB;
(2)解:∵△ABD≌△CFD,∴BD=DF,AD=DC,
∵BC=7,AD=5,∴BD=BC CD=2,∴AF=AD DF=5 2=3.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
