2022-2023学年人教版八年级数学上册13.1.2 线段的垂直平分线的性质 导学案(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册13.1.2 线段的垂直平分线的性质 导学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 232.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 00:00:00 | ||
图片预览



文档简介
13.1.2线段的垂直平分线的性质
【学习目标】
1.了解两个图形成轴对称的性质,了解轴对称图形的性质。探究线段垂直平分线的性质。
2.经历探索轴对称图形性质的过程,发展空间观察能力。
3.体验数学与现实间的联系,发展审美感,激发兴趣。
【学习重难点】
轴对称的性质,线段垂直平分线的性质。
【学习过程】
一、知识链接。
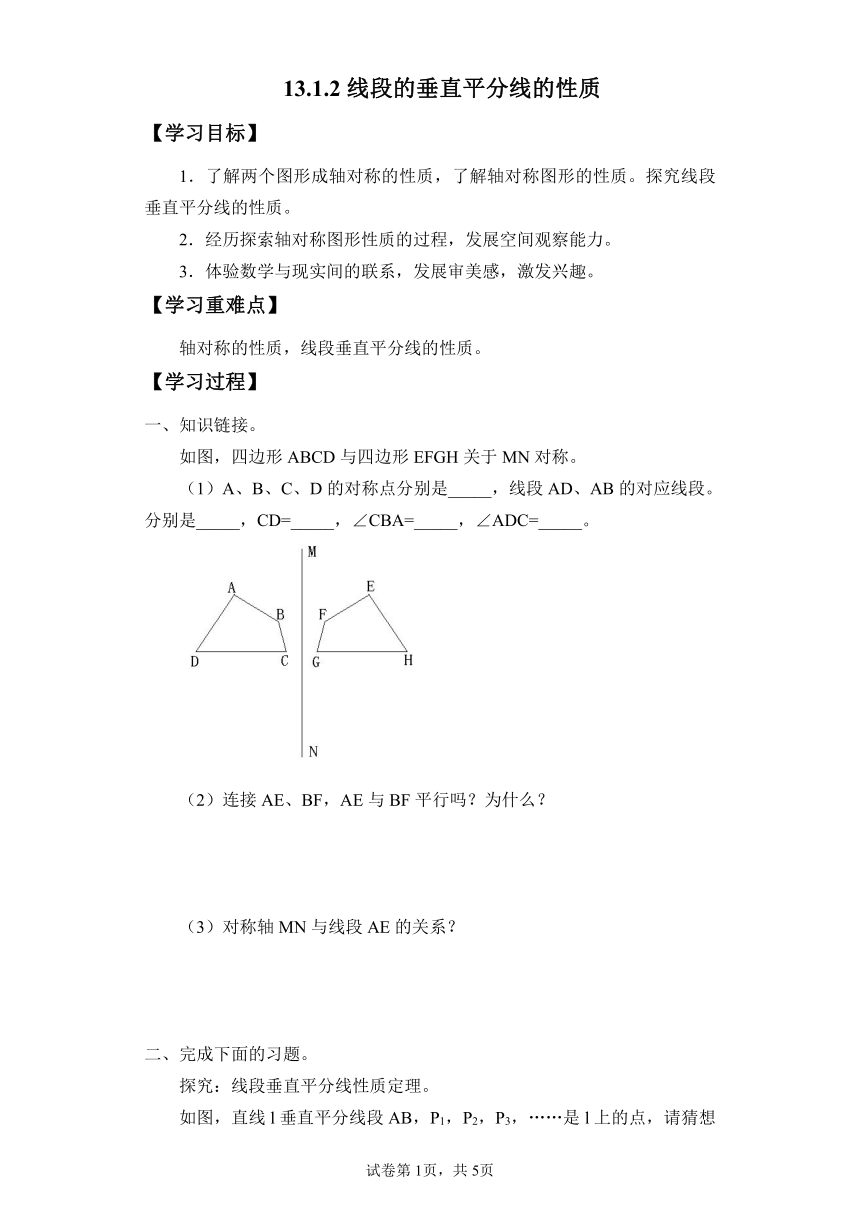
如图,四边形ABCD与四边形EFGH关于MN对称。
(1)A、B、C、D的对称点分别是_____,线段AD、AB的对应线段。分别是_____,CD=_____,∠CBA=_____,∠ADC=_____。
(2)连接AE、BF,AE与BF平行吗?为什么?
(3)对称轴MN与线段AE的关系?
二、完成下面的习题。
探究:线段垂直平分线性质定理。
如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,请猜想点P1,P2,P3,……到点A与点B的距离之间的数量关系并证明你的猜想。
猜想:_____。
已知:直线l垂直平分_____,垂足为O,点C在直线l上,求证:AC=_____。
证明:
线段垂直平分线性质定理_____
几何语言:∵_____
∴_____
跟踪训练:如图所示,直线MN和DE分别是线段AB、BC的垂直平分线,它们交于P点,请问PA和PC相等吗?为什么?
三、线段垂直平分线判定定理。
你能写出线段垂直平分线的性质定理的逆命题吗?_____。
小帅同学为验证逆命题已经做出了一些步骤,请你帮他补充完整。
已知:_____=_____求证:_____在AB的_____线上。
判定定理:_____
几何语言:∵_____
∴_____
四、练习题。
1.三角形的外心是三角形的( )
A.三条中线的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三条高所在直线的交点
2.如图,在中,,以点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于长为半径画弧,两弧交于点,作射线,交于点,连接,.给出下列说法:①;②垂直平分;③平分;④.其中正确的有( )
A.①② B.②③ C.③④ D.②④
3.如图,DE,DF分别是线段AB,BC的垂直平分线,连接DA,DC,则( )
A.∠A=∠C B.∠B=∠ADC
C.DA=DC D.DE=DF
4.如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( )
A.在∠B的平分线与DE的交点处
B.在线段AB、AC的垂直平分线的交点处
C.在∠B的平分线与DE的垂直平分线的交点处
D.在∠A的平分线与DE的垂直平分线的交点处
5.如图,在Rt△ABC中,∠ABC=90°,分别以点A和点B为圆心,大于AB的长为半径作弧相交于点D和点E,直线DE交AC于点F,交AB于点G,连接BF,若BF=3,AG=2,则BC=( )
A.5 B.4 C.2 D.2
6.如图所示线段AB,BC的垂直平分线的交点P恰好在AC边上,且,则点B到点P的距离为________.
7.如图,在四边形ABCD中,AD=CD,AB=CB.下列结论:①BD垂直平分AC;②BD平分∠ADC;③ABCD;④ABD≌CBD.其中所有正确结论的序号是_______.
8.如图,DE是△ABC的边AB的垂直平分线,垂足为点D,DE交AC于点E,且,△BEC的周长为11,则BC的长为________.
9.如图,在中,是的中垂线,分别交,于点,.若的周长为8,,求的长.
10.如图,在中,,,通过尺规作图,得到直线和射线,仔细观察作图痕迹,完成下列问题:
(1)直线是线段的________线,射线是的________线;
(2)求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.A
3.C
4.C
5.C
6.5cm
7.①②④
8.4
9.5
10.(1)线段垂直平分;角平分
(2)23°
4 / 4
【学习目标】
1.了解两个图形成轴对称的性质,了解轴对称图形的性质。探究线段垂直平分线的性质。
2.经历探索轴对称图形性质的过程,发展空间观察能力。
3.体验数学与现实间的联系,发展审美感,激发兴趣。
【学习重难点】
轴对称的性质,线段垂直平分线的性质。
【学习过程】
一、知识链接。
如图,四边形ABCD与四边形EFGH关于MN对称。
(1)A、B、C、D的对称点分别是_____,线段AD、AB的对应线段。分别是_____,CD=_____,∠CBA=_____,∠ADC=_____。
(2)连接AE、BF,AE与BF平行吗?为什么?
(3)对称轴MN与线段AE的关系?
二、完成下面的习题。
探究:线段垂直平分线性质定理。
如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,请猜想点P1,P2,P3,……到点A与点B的距离之间的数量关系并证明你的猜想。
猜想:_____。
已知:直线l垂直平分_____,垂足为O,点C在直线l上,求证:AC=_____。
证明:
线段垂直平分线性质定理_____
几何语言:∵_____
∴_____
跟踪训练:如图所示,直线MN和DE分别是线段AB、BC的垂直平分线,它们交于P点,请问PA和PC相等吗?为什么?
三、线段垂直平分线判定定理。
你能写出线段垂直平分线的性质定理的逆命题吗?_____。
小帅同学为验证逆命题已经做出了一些步骤,请你帮他补充完整。
已知:_____=_____求证:_____在AB的_____线上。
判定定理:_____
几何语言:∵_____
∴_____
四、练习题。
1.三角形的外心是三角形的( )
A.三条中线的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三条高所在直线的交点
2.如图,在中,,以点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于长为半径画弧,两弧交于点,作射线,交于点,连接,.给出下列说法:①;②垂直平分;③平分;④.其中正确的有( )
A.①② B.②③ C.③④ D.②④
3.如图,DE,DF分别是线段AB,BC的垂直平分线,连接DA,DC,则( )
A.∠A=∠C B.∠B=∠ADC
C.DA=DC D.DE=DF
4.如图,三条笔直的公路两两相交,交点分别在点A、B、C处,有两户村民分别在点D和点E处,现准备建造一个蓄水池,要求水池到两条公路AB、BC的距离相等,且到两户村民D、E的距离相等,则水池修建的位置应该是( )
A.在∠B的平分线与DE的交点处
B.在线段AB、AC的垂直平分线的交点处
C.在∠B的平分线与DE的垂直平分线的交点处
D.在∠A的平分线与DE的垂直平分线的交点处
5.如图,在Rt△ABC中,∠ABC=90°,分别以点A和点B为圆心,大于AB的长为半径作弧相交于点D和点E,直线DE交AC于点F,交AB于点G,连接BF,若BF=3,AG=2,则BC=( )
A.5 B.4 C.2 D.2
6.如图所示线段AB,BC的垂直平分线的交点P恰好在AC边上,且,则点B到点P的距离为________.
7.如图,在四边形ABCD中,AD=CD,AB=CB.下列结论:①BD垂直平分AC;②BD平分∠ADC;③ABCD;④ABD≌CBD.其中所有正确结论的序号是_______.
8.如图,DE是△ABC的边AB的垂直平分线,垂足为点D,DE交AC于点E,且,△BEC的周长为11,则BC的长为________.
9.如图,在中,是的中垂线,分别交,于点,.若的周长为8,,求的长.
10.如图,在中,,,通过尺规作图,得到直线和射线,仔细观察作图痕迹,完成下列问题:
(1)直线是线段的________线,射线是的________线;
(2)求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.A
3.C
4.C
5.C
6.5cm
7.①②④
8.4
9.5
10.(1)线段垂直平分;角平分
(2)23°
4 / 4
