2022-2023学年人教版八年级数学上册13.4 课题学习 最短路径问题 导学案(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册13.4 课题学习 最短路径问题 导学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 99.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 07:07:27 | ||
图片预览

文档简介
13.4课题学习 最短路径问题
【学习目标】
能利用轴对称解决简单的最短路径问题。
【学习重难点】
1.如何证明所作的路径是最短的。
【学习过程】
一、预习感知。
1.举出常见的轴对称图形:_____(至少写三个)。
2.轴对称图形上任意一对对应点的连线被_____垂直平分。
3.等腰三角形的“三线合一”是指_____,_____,_____互相重合。
4.两个全等的图形__________轴对称。(填“是”、“不是”、“不一定是”)
5.线段垂直平分线上的点到__________________________的距离相等。
二、合作探究。
(一)最短路径问题。
(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求。
(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求。
(二)运用轴对称解决距离最短问题。
运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点到直线上某点的距离和最小这个核心,所有作法都相同。
(三)利用平移确定最短路径选址。
解决连接河两岸的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题。
三、检查反馈。
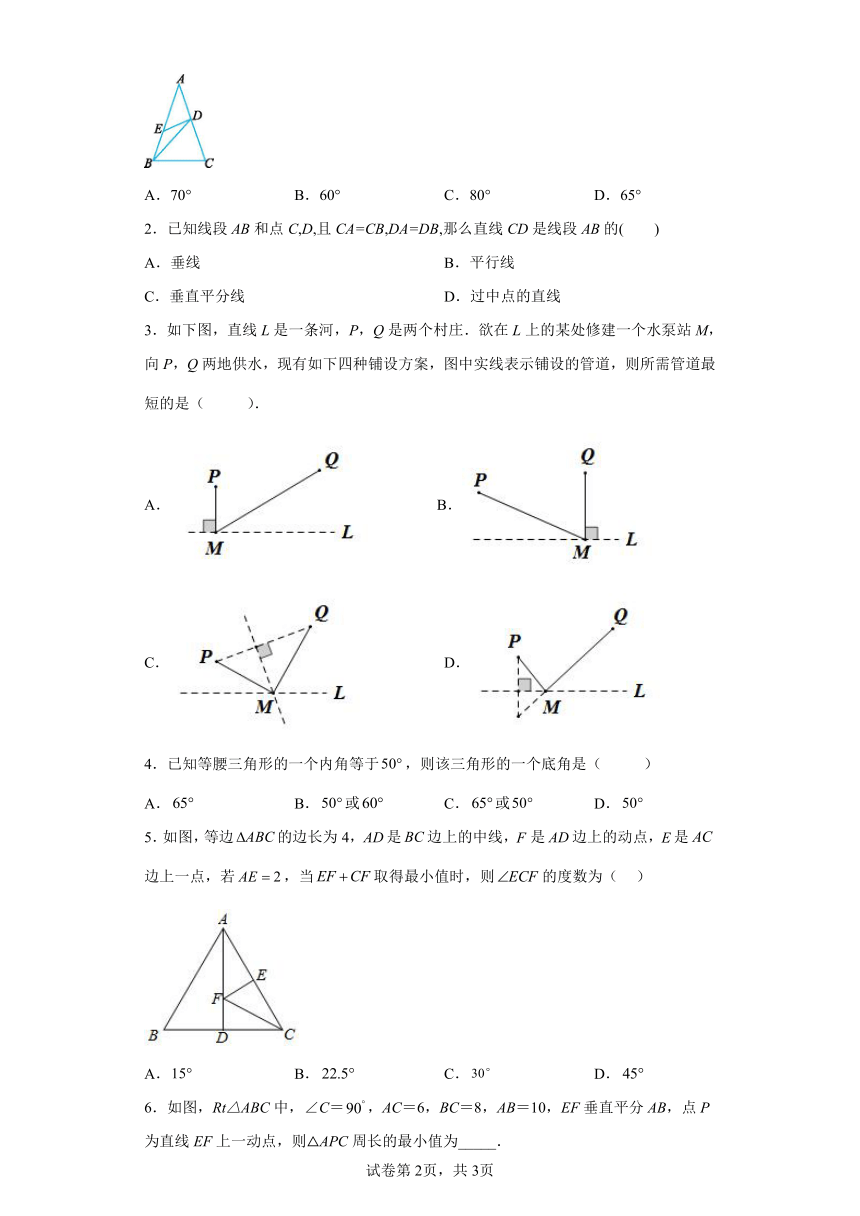
1.如图所示,△ABC中,AB=AC,∠EBD=20°,AD=DE=EB,则∠C的度数为( )
A.70° B.60° C.80° D.65°
2.已知线段AB和点C,D,且CA=CB,DA=DB,那么直线CD是线段AB的( )
A.垂线 B.平行线
C.垂直平分线 D.过中点的直线
3.如下图,直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站M,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).
A. B.
C. D.
4.已知等腰三角形的一个内角等于,则该三角形的一个底角是( )
A. B.或 C.或 D.
5.如图,等边的边长为4,是边上的中线,是边上的动点,是边上一点,若,当取得最小值时,则的度数为( )
A. B. C. D.
6.如图,Rt△ABC中,∠C=,AC=6,BC=8,AB=10,EF垂直平分AB,点P为直线EF上一动点,则△APC周长的最小值为_____.
7.如图,在边长为6,面积为的等边△ABC中,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点, 连结BM、MN,则BM+MN的最小值是_______
8.如下图,,在、上分别找一点M、N,当周长最小时,的度数是_____________.
9.如图,在△ABC中,AB=AC,AD是△ABC底边BC上的中线,点P为线段AB上一点.若点P为AB的中点,当∠BPE满足什么条件时,△ABC是等边三角形,
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.C
3.D
4.C
5.C
6.14
7.
8.120°
9.∠BPE=90°
3 / 3
【学习目标】
能利用轴对称解决简单的最短路径问题。
【学习重难点】
1.如何证明所作的路径是最短的。
【学习过程】
一、预习感知。
1.举出常见的轴对称图形:_____(至少写三个)。
2.轴对称图形上任意一对对应点的连线被_____垂直平分。
3.等腰三角形的“三线合一”是指_____,_____,_____互相重合。
4.两个全等的图形__________轴对称。(填“是”、“不是”、“不一定是”)
5.线段垂直平分线上的点到__________________________的距离相等。
二、合作探究。
(一)最短路径问题。
(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求。
(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求。
(二)运用轴对称解决距离最短问题。
运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点到直线上某点的距离和最小这个核心,所有作法都相同。
(三)利用平移确定最短路径选址。
解决连接河两岸的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题。
三、检查反馈。
1.如图所示,△ABC中,AB=AC,∠EBD=20°,AD=DE=EB,则∠C的度数为( )
A.70° B.60° C.80° D.65°
2.已知线段AB和点C,D,且CA=CB,DA=DB,那么直线CD是线段AB的( )
A.垂线 B.平行线
C.垂直平分线 D.过中点的直线
3.如下图,直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站M,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).
A. B.
C. D.
4.已知等腰三角形的一个内角等于,则该三角形的一个底角是( )
A. B.或 C.或 D.
5.如图,等边的边长为4,是边上的中线,是边上的动点,是边上一点,若,当取得最小值时,则的度数为( )
A. B. C. D.
6.如图,Rt△ABC中,∠C=,AC=6,BC=8,AB=10,EF垂直平分AB,点P为直线EF上一动点,则△APC周长的最小值为_____.
7.如图,在边长为6,面积为的等边△ABC中,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点, 连结BM、MN,则BM+MN的最小值是_______
8.如下图,,在、上分别找一点M、N,当周长最小时,的度数是_____________.
9.如图,在△ABC中,AB=AC,AD是△ABC底边BC上的中线,点P为线段AB上一点.若点P为AB的中点,当∠BPE满足什么条件时,△ABC是等边三角形,
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.C
3.D
4.C
5.C
6.14
7.
8.120°
9.∠BPE=90°
3 / 3
