2022-2023学年人教版八年级数学上册13.4 课题学习 最短路径问题 导学案 (含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册13.4 课题学习 最短路径问题 导学案 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 397.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 07:08:18 | ||
图片预览


文档简介
13.4最短路径问题
【学习目标】
体会利用作图解决最短路径问题
【学法指导】
最短路径问题,通过转化为两点之间线段最短加以解决。
【学习过程】
一、预习导学
1.如图所示,从A地到B地有三条路可供选择,你会选走哪条路最近?你的理由是什么?
二、合作探究
探究一
1.两点在一条直线异侧
已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB最小。
思考:为什么这样做就能得到最短距离呢?你如何验证PA+PB最短呢?
2.到同侧两点距离和最短
如图所示,要在街道旁修建一个奶站P,向居民区A、B提供牛奶,奶站P应建在什么地方,才能使从A、B到它的距离之和最短。
。B
A 。
思考:为什么这样做就能得到最短距离呢?你如何验证PA+PB最短呢?
探究二
3.造桥选址问题中的最短路径问题
如图,A和B连地在一条河的两岸,要在河上造一座桥MN,桥造在何处可使从A到B路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
归纳总结:在解决最短路径问题是,我们通常利用 、 等变化把已知问题转化为容易解决的问题,从而作出最短路径的选择。
【达标检测】
1.下列三角形中,等腰三角形的个数是( )
A.4个 B.3个 C.2个 D.1个
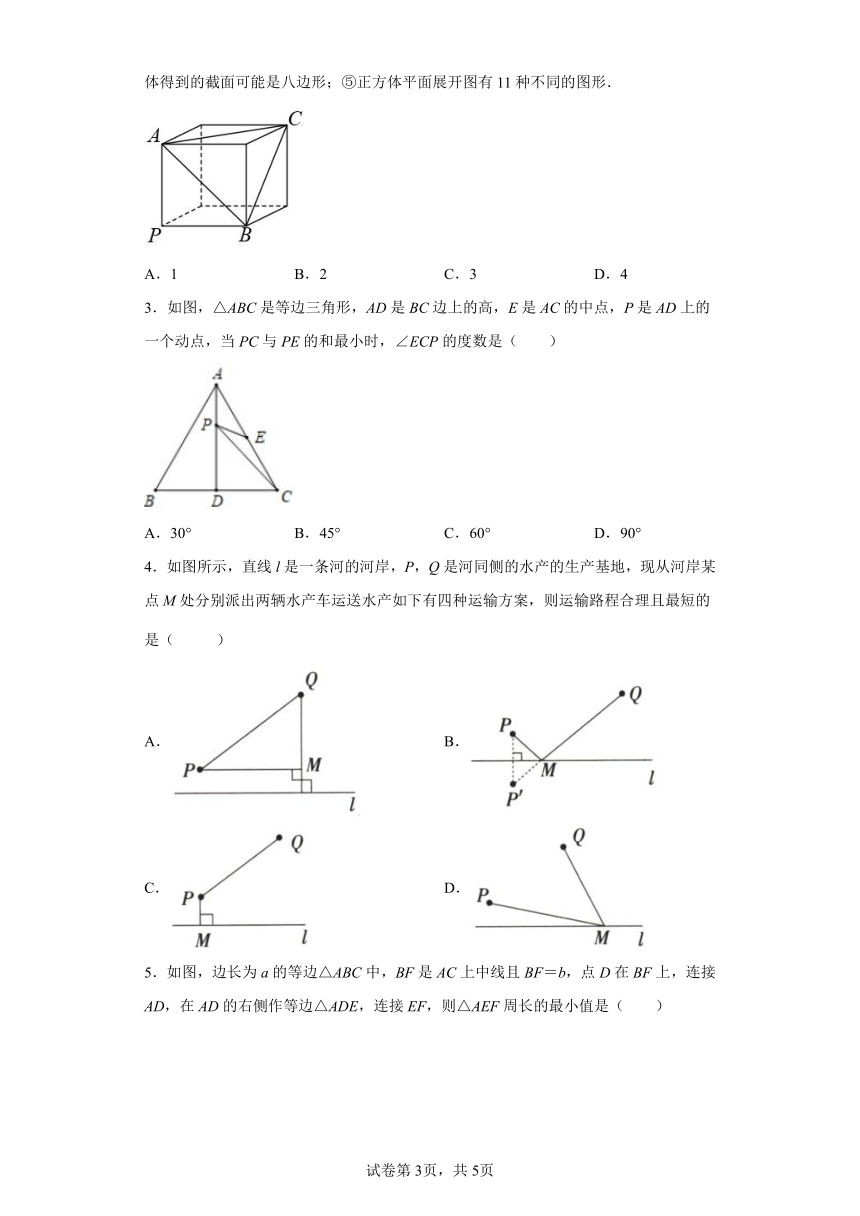
2.如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有( )个
①用剪刀沿着它的棱剪开这个纸盒,至少要剪7刀,才能展开成平面图形;②用一平面去截这个正方体得到的截面是三角形ABC,则∠ABC=45°;③一只蚂蚁在一个实心正方体木块P点处想沿着表面爬到C点最近的路只有4条;④用一平面去截这个正方体得到的截面可能是八边形;⑤正方体平面展开图有11种不同的图形.
A.1 B.2 C.3 D.4
3.如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠ECP的度数是( )
A.30° B.45° C.60° D.90°
4.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
5.如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是( )
A.ab B.a+b C.ab D.a
6.如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是 _____.
7.如图,在中,垂直平分,点P为直线上一动点,则周长的最小值是________.
8.已知,如图,在直线l的两侧有两点A、B在直线上画出点P,使PA+PB最短,画法:______.
9.如图,在长度为1个单位长度的小正方形组成的网格中,点A,B,C均在小正方形的顶点上.
直接写出△A'B'C′的面积为 ;
10.如图,在△ABC中,AB=AC,点D是BC的中点,点E在AB上,BE=BD,∠BAC=76°,求∠ADE的大小.
参考答案:
1.B
2.B
3.A
4.B
5.B
6.4
7.7
8.连接AB交直线l于P
9.3.5
10.26°
①
②
③
试卷第1页,共3页
试卷第1页,共3页
【学习目标】
体会利用作图解决最短路径问题
【学法指导】
最短路径问题,通过转化为两点之间线段最短加以解决。
【学习过程】
一、预习导学
1.如图所示,从A地到B地有三条路可供选择,你会选走哪条路最近?你的理由是什么?
二、合作探究
探究一
1.两点在一条直线异侧
已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB最小。
思考:为什么这样做就能得到最短距离呢?你如何验证PA+PB最短呢?
2.到同侧两点距离和最短
如图所示,要在街道旁修建一个奶站P,向居民区A、B提供牛奶,奶站P应建在什么地方,才能使从A、B到它的距离之和最短。
。B
A 。
思考:为什么这样做就能得到最短距离呢?你如何验证PA+PB最短呢?
探究二
3.造桥选址问题中的最短路径问题
如图,A和B连地在一条河的两岸,要在河上造一座桥MN,桥造在何处可使从A到B路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
归纳总结:在解决最短路径问题是,我们通常利用 、 等变化把已知问题转化为容易解决的问题,从而作出最短路径的选择。
【达标检测】
1.下列三角形中,等腰三角形的个数是( )
A.4个 B.3个 C.2个 D.1个
2.如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有( )个
①用剪刀沿着它的棱剪开这个纸盒,至少要剪7刀,才能展开成平面图形;②用一平面去截这个正方体得到的截面是三角形ABC,则∠ABC=45°;③一只蚂蚁在一个实心正方体木块P点处想沿着表面爬到C点最近的路只有4条;④用一平面去截这个正方体得到的截面可能是八边形;⑤正方体平面展开图有11种不同的图形.
A.1 B.2 C.3 D.4
3.如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠ECP的度数是( )
A.30° B.45° C.60° D.90°
4.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
5.如图,边长为a的等边△ABC中,BF是AC上中线且BF=b,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,则△AEF周长的最小值是( )
A.ab B.a+b C.ab D.a
6.如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是 _____.
7.如图,在中,垂直平分,点P为直线上一动点,则周长的最小值是________.
8.已知,如图,在直线l的两侧有两点A、B在直线上画出点P,使PA+PB最短,画法:______.
9.如图,在长度为1个单位长度的小正方形组成的网格中,点A,B,C均在小正方形的顶点上.
直接写出△A'B'C′的面积为 ;
10.如图,在△ABC中,AB=AC,点D是BC的中点,点E在AB上,BE=BD,∠BAC=76°,求∠ADE的大小.
参考答案:
1.B
2.B
3.A
4.B
5.B
6.4
7.7
8.连接AB交直线l于P
9.3.5
10.26°
①
②
③
试卷第1页,共3页
试卷第1页,共3页
