2.11 有理数的乘方 课件(共17张PPT)
文档属性
| 名称 | 2.11 有理数的乘方 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 13:49:33 | ||
图片预览






文档简介
(共17张PPT)
2.11 有理数的乘方
华师大版 七年级上册
教学目标
【教学目标】
1.理解有理数乘方的意义,了解幂、底数、指数的相关概念;
2.掌握有理数的乘方的符号法则及相关性质,能够正确地进行有理数的乘方运算;
3.在经历发现问题、探索规律的过程中体会到数学学习的乐趣,从而培养学生学习数学的主动性和勇于探索的精神,增进学生学好数学的自信心.
【重点】有理数乘方的意义及其运算.
【难点】有理数乘方符号法则及相关性质的理解与应用.
新知导入
计算
(1) (-2)+(-2)+(-2)=
(2) (-2)+(-2)+(-2) + (-2 )=
(3) (-2)+(-2)+(-2) + (-2 ) +(-2)+(-2) + (-2)+(-2)+(-2) + (-2 ) =
(-2)×3
(-2)×4
(-2)×10
新知导入
2.如图,一正方体的棱长为a厘米, 则它的体积为__________立方厘米.
a×a×a
1.如图,边长为a厘米的正方形的面积为______平方厘米.
a×a
a
a
在小学已经知道:
a×a=
a×a×a=
读作:a的平方(或a的2次方)
读作:a的立方(或a的3次方)
a2
a3
新知讲解
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a· ·a = an
n个
…
例如:2×2×2×2
2×2×2×2×2×2
记作
记作
读作2的6次方(幂).
读作2的4次方(幂).
新知讲解
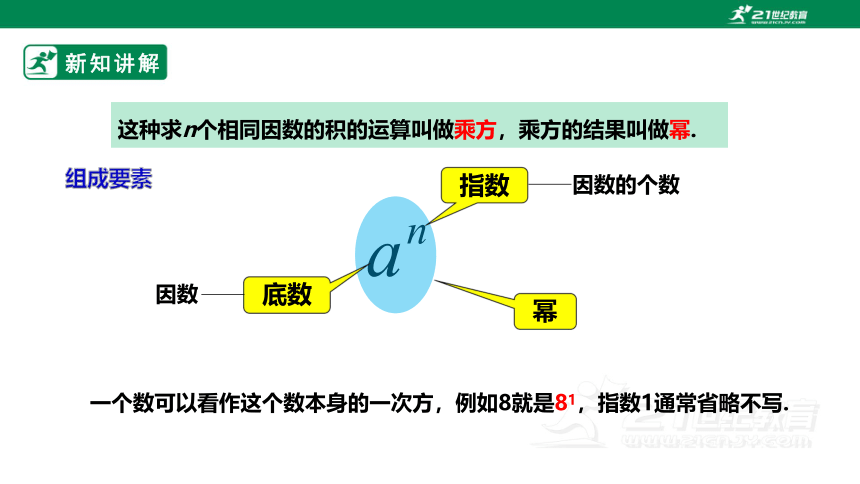
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方,例如8就是81,指数1通常省略不写.
组成要素
幂
指数
底数
因数
因数的个数
新知讲解
23与32的一样吗?为什么?
23中,底数是2,指数是3
32中,底数是3,指数是2
新知讲解
例 计算
(1)(-2)3 (2)(-2)4 (3)(-2)5
解:(1)(-2)3 =(-2)×(-2)×(-2)=-8
(2)(-2)4 =(-2)×(-2)×(-2)×(-2)=16
(3)(-2)5=(-2)×(-2)×(-2)×(-2)×(-2)=-32
新知讲解
(-2)3与-23的意义是否相同?
(-2)4与-24呢?
-23读作23的相反数,而(-2)3读作-2的三次方。
-24读作24的相反数,而(-2)4读作-2的四次方。
新知讲解
根据有理数乘法法则,我们有:
正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数.
1的任何次幂都是1.
-1的偶次幂是1,奇次幂是-1.
确定幂的符号时,一看底数,
二看指数.
课堂练习
1.填空:
(1)把(-5)×(-5) ×(-5)写成幂的形式是_______,底数是____,指数是____,结果是______;
(2)在45中,底数是____,指数是____,结果是_________;
(3)在 中,底数是____,指数是____,结果是____.
(-5)3
-5
3
-125
4
5
1024
-
6
课堂练习
2. 下列运算正确的是( )
A.-22=4 B.3=-8
C.3=- D. (-2)3=-6
C
3.一个非零整数的平方和立方都等于它的绝对值,这个数是( )
A. -1 B. 2 C. 1 D. -1或1
C
课堂练习
4.计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
课堂练习
5.计算:(1)(-6)3×(- ); (2)(-3)3×(- )2.
解:(1)原式=(-216)×
=216×
=36;
(2)原式=-27×
=-3.
课堂总结
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数.
(2)负数的奇次幂是负数,负数的偶次幂是正数.
(3)零的正整数次幂都是零.
幂
指数
底数
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.11 有理数的乘方
华师大版 七年级上册
教学目标
【教学目标】
1.理解有理数乘方的意义,了解幂、底数、指数的相关概念;
2.掌握有理数的乘方的符号法则及相关性质,能够正确地进行有理数的乘方运算;
3.在经历发现问题、探索规律的过程中体会到数学学习的乐趣,从而培养学生学习数学的主动性和勇于探索的精神,增进学生学好数学的自信心.
【重点】有理数乘方的意义及其运算.
【难点】有理数乘方符号法则及相关性质的理解与应用.
新知导入
计算
(1) (-2)+(-2)+(-2)=
(2) (-2)+(-2)+(-2) + (-2 )=
(3) (-2)+(-2)+(-2) + (-2 ) +(-2)+(-2) + (-2)+(-2)+(-2) + (-2 ) =
(-2)×3
(-2)×4
(-2)×10
新知导入
2.如图,一正方体的棱长为a厘米, 则它的体积为__________立方厘米.
a×a×a
1.如图,边长为a厘米的正方形的面积为______平方厘米.
a×a
a
a
在小学已经知道:
a×a=
a×a×a=
读作:a的平方(或a的2次方)
读作:a的立方(或a的3次方)
a2
a3
新知讲解
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a· ·a = an
n个
…
例如:2×2×2×2
2×2×2×2×2×2
记作
记作
读作2的6次方(幂).
读作2的4次方(幂).
新知讲解
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方,例如8就是81,指数1通常省略不写.
组成要素
幂
指数
底数
因数
因数的个数
新知讲解
23与32的一样吗?为什么?
23中,底数是2,指数是3
32中,底数是3,指数是2
新知讲解
例 计算
(1)(-2)3 (2)(-2)4 (3)(-2)5
解:(1)(-2)3 =(-2)×(-2)×(-2)=-8
(2)(-2)4 =(-2)×(-2)×(-2)×(-2)=16
(3)(-2)5=(-2)×(-2)×(-2)×(-2)×(-2)=-32
新知讲解
(-2)3与-23的意义是否相同?
(-2)4与-24呢?
-23读作23的相反数,而(-2)3读作-2的三次方。
-24读作24的相反数,而(-2)4读作-2的四次方。
新知讲解
根据有理数乘法法则,我们有:
正数的任何次幂都是正数;
负数的奇次幂是负数,负数的偶次幂是正数.
1的任何次幂都是1.
-1的偶次幂是1,奇次幂是-1.
确定幂的符号时,一看底数,
二看指数.
课堂练习
1.填空:
(1)把(-5)×(-5) ×(-5)写成幂的形式是_______,底数是____,指数是____,结果是______;
(2)在45中,底数是____,指数是____,结果是_________;
(3)在 中,底数是____,指数是____,结果是____.
(-5)3
-5
3
-125
4
5
1024
-
6
课堂练习
2. 下列运算正确的是( )
A.-22=4 B.3=-8
C.3=- D. (-2)3=-6
C
3.一个非零整数的平方和立方都等于它的绝对值,这个数是( )
A. -1 B. 2 C. 1 D. -1或1
C
课堂练习
4.计算:
(1) (-4)3; (2) (-2)4; (3)
解:(1) (-4)3=(-4)×(-4)×(-4)=-64;
(2) (-2)4=(-2)×(-2)×(-2)×(-2)=16;
课堂练习
5.计算:(1)(-6)3×(- ); (2)(-3)3×(- )2.
解:(1)原式=(-216)×
=216×
=36;
(2)原式=-27×
=-3.
课堂总结
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数.
(2)负数的奇次幂是负数,负数的偶次幂是正数.
(3)零的正整数次幂都是零.
幂
指数
底数
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
