总复习四 (圆)课件人教版六年级上册数学(共31张PPT)
文档属性
| 名称 | 总复习四 (圆)课件人教版六年级上册数学(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 735.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-31 18:40:11 | ||
图片预览







文档简介
(共31张PPT)
圆知识点总复习
圆与各部分之间的关系
长方形/正方形里剪最大圆
等周长变形
目
录
半圆的周长和面积
求阴影部分面积
解决问题
考点一
圆与各部分之间的关系
考点一:圆与各部分之间的关系
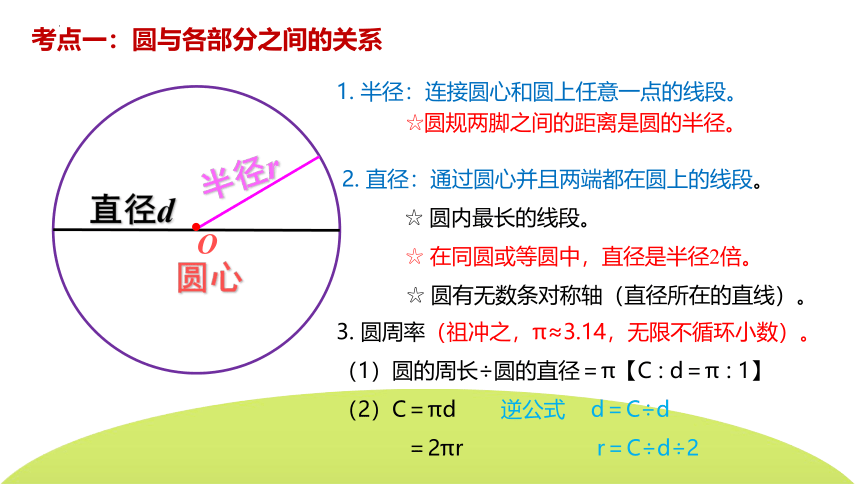
1. 半径:连接圆心和圆上任意一点的线段。
☆圆规两脚之间的距离是圆的半径。
O
圆心
半径r
直径d
·
2. 直径:通过圆心并且两端都在圆上的线段。
☆ 圆内最长的线段。
☆ 在同圆或等圆中,直径是半径2倍。
☆ 圆有无数条对称轴(直径所在的直线)。
3. 圆周率(祖冲之,π≈3.14,无限不循环小数)。
(1)圆的周长÷圆的直径=π【C : d=π : 1】
(2)C=πd 逆公式 d=C÷d
=2πr r=C÷d÷2
考点一:圆与各部分之间的关系
圆心(O) 用圆规画圆时,针尖所在的位置
半径(r) 连接圆心和圆上任意一点的线段
半径的长度就是圆规两脚之间的距离
直径(d) 通过圆心并且两端都在圆上的线段
圆周率(π) 任意一个圆的周长与它的直径的比值
它是一个无限不循环小数
考点一:圆与各部分之间的关系
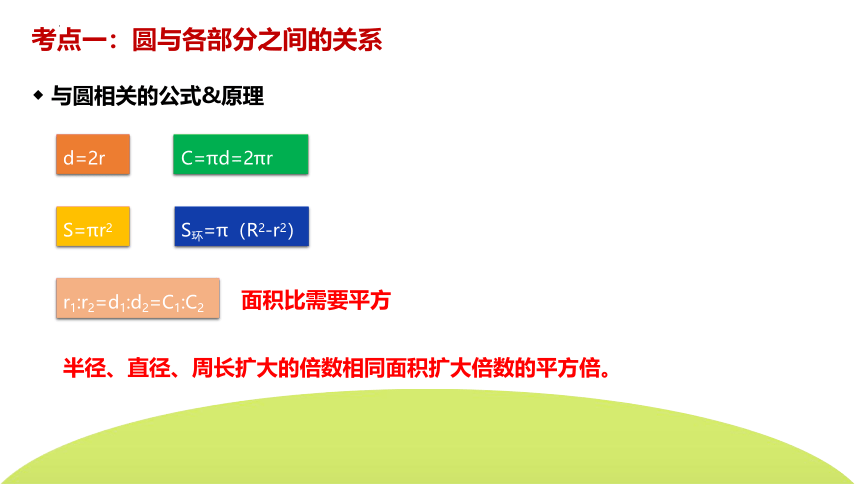
◆ 与圆相关的公式&原理
d=2r
C=πd=2πr
S=πr2
S环=π(R2-r2)
r1:r2=d1:d2=C1:C2
半径、直径、周长扩大的倍数相同面积扩大倍数的平方倍。
面积比需要平方
【某区真题】填空题。
1. 若圆的半径扩大3倍,那么直径扩大( )倍,周长扩大( )倍,面积
扩大( )倍。
3
3
9
2. 小圆半径是大圆半径的 ,那么小圆直径是大圆直径的 ,小圆周长
是大圆周长的 ,小圆面积是大圆面积的 。
3
4
3
4
9
16
考点二
长方形/正方形里剪最大的圆
考点二:长方形/正方形里剪最大的圆
长方形:短边就是圆的直径
正方形:边长就是圆的直径
在一个边长为4分米的正方形里剪下一个最大的圆,这个圆的周长是( )分米,面积是( )平方分米。
12.56
12.56
d=4,r=2
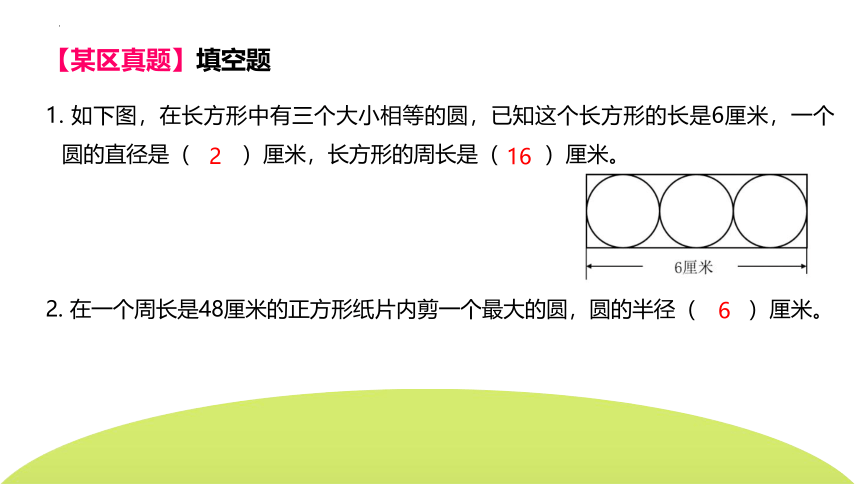
【某区真题】填空题
1. 如下图,在长方形中有三个大小相等的圆,已知这个长方形的长是6厘米,一个圆的直径是( )厘米,长方形的周长是( )厘米。
2. 在一个周长是48厘米的正方形纸片内剪一个最大的圆,圆的半径( )厘米。
2
16
6
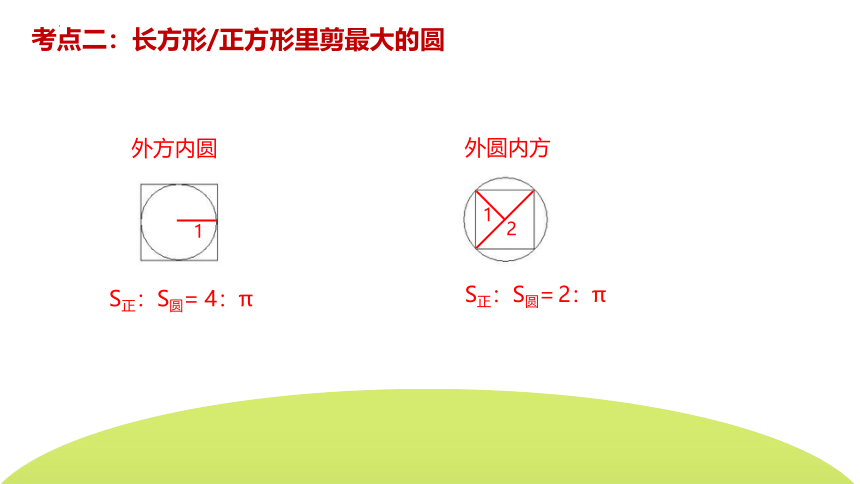
考点二:长方形/正方形里剪最大的圆
外方内圆
S正:S圆=
外圆内方
S正:S圆=
1
1
2
4:π
2:π
【某区真题】填空题
1. 如右图,在一个边长为10厘米的正方形纸片中剪下一个最大的圆,这个圆的
面积是( )平方厘米,剩下部分的面积是( )平方厘米,圆的
面积与正方形纸片的面积比是( )。
直径:10cm
半径:5cm
78.5
21.5
π : 4
【某区真题】填空题
2. 已知圆内最大的正方形的面积是30平方厘米,这个圆的面积是( )
平方厘米。
一份面积:30÷2=15 cm
圆:15×3.14=47.1 cm
47.1
考点三
等周长变形
考点三:等周长变形
识记:周长相等的长方形、正方形和圆,S圆>S正>S长
12.56÷4=3.14(厘米)
C=πd
=3.14×4
=12.56(厘米)
一根铁丝刚好能围成一个直径是4厘米的圆,若把它围成一个正方形,正方形的边长是( )厘米。
考点四
半圆的周长和面积
考点四:半圆的周长和面积
C半圆=πd÷2+d
=πr + 2r
=5.14r
【注意是否有靠墙的情况,靠墙时不用加d】
S半圆=πr ÷2
·
·
r
r
S圆=πr
C圆=πd
=2πr
圆周长的一半(πr)
1. 求图中半圆的周长与面积。(单位:厘米)
C半=πd÷2+d
=πr+2r
S半=πr2÷2
C半=3.14×3+2×3
=15.42(厘米)
S半=3.14×32÷2
=14.13(平方厘米)
【某区真题】
【某区真题】
2. 靠墙用篱笆围一个半圆形的菜地,菜地的直径是3米,需要多少米的篱笆?
3.14×3÷2=4.71(米)
答:需要4.71米。
【某区真题】
3. 一个半圆形花坛,周长是10.28米。这个花坛的面积是多少平方米?
r: 10.28÷(3.14+2)=2(米)
3.14×2 ÷2=6.28(平方米)
答:这个花坛的面积是6.28平方米。
考点五
求阴影部分的面积
考点四:求阴影部分的面积
1. 求组合图形的周长常用方法:
☆描边法:曲线部分(圆的周长×几分之几)+线段部分
2. 求组合图形的面积常用方法:
①直接计算;
②小+小;
③大-小。
☆ 六大基本图形的面积计算:
①S长=ab; ④S三=ah÷2;
②S正=a ; ⑤S梯=(a+b)h÷2;
③S平=ah; ⑥S圆=πr
考点四:求阴影部分的面积
4. 扇形的周长和面积
① 先找出圆心角以及圆心角占整个圆的几分之几;
② 算出整个圆的周长或面积,再求它的几分之几是多少。
3. 一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
圆心角:顶点在圆心的角叫圆心角。
☆半径和圆心角决定扇形的大小;
圆心角相等,半径越长,扇形面积越大。
n°
【某区真题】
S长:8×(8÷2)=32(cm2)
r=3cm,R=3+2=5cm
1. 求阴影部分面积。
S环=π(R2-r2)
=3.14×(32-22)
=50.24(cm2)
S半:3.14×(8÷2)2÷2=25.12(cm2)
S阴:32-25.12=6.88(cm2)
【某区真题】
2. 求下图阴影部分的面积。
3.14×8 × =150.72(平方厘米)
S半圆: 3.14×(8÷2)2÷2
=50.24÷2
=25.12(平方厘米)
S梯形:(10+12)×8÷2=88(平方厘米)
88-25.12=62.88(平方厘米)
考点六
解决问题
考点六:解决问题
1. 车轮问题。
(1)车轮滚动一周的长度,就是这个车轮的周长。(C=πd=2πr)
(2)速度:周长×每分钟转的圈数。
(3)路程÷速度=时间【单位统一】
2. 时钟问题【针的长度=半径】:
(1)分针走一圈,1小时; (2) 时针走一圈,12小时;一昼夜=24小时。
① 先算一圈(C=2πr) ① 先算一圈(C=2πr)
② 周长×小时数(或“×分钟÷60“) ② 周长×小时数÷12
【某区真题】
1. 一辆自行车轮胎的外直径是0.7m,如果车轮平均每分钟转100周。4分钟后自行车行进了多少米?
3.14×0.7=2.198(米)
2.198×100×4=879.2(米)
答:4分钟后自行车行进了879.2米。
【某区真题】
2. 一个运动场(如图),两端是半圆形,中间是长方形。
(1)沿着这个运动场跑1圈,要跑多少米?
(2)给这个运动场铺上草坪,一共要铺草坪多少平方米?
(1)3.14×60+100×2=388.4(米)
答:沿着这个运动场跑1圈,要跑388.4米。
(2)3.14×(60÷2) +100×60=8826(平方米)
答:给这个运动场铺上草坪,一共要铺草坪8826平方米。
【某区真题】
3. 时钟的分针长20cm,经过2小时,这跟分针的针尖走了多少厘米?扫过地面积是多少平方厘米?
2×3.14×20×2=251.2(厘米)
3.14×202×2=2512(平方厘米)
答:分针的针尖走了251.2厘米,扫过地面积是2512平方厘米。
感谢观看
圆知识点总复习
圆与各部分之间的关系
长方形/正方形里剪最大圆
等周长变形
目
录
半圆的周长和面积
求阴影部分面积
解决问题
考点一
圆与各部分之间的关系
考点一:圆与各部分之间的关系
1. 半径:连接圆心和圆上任意一点的线段。
☆圆规两脚之间的距离是圆的半径。
O
圆心
半径r
直径d
·
2. 直径:通过圆心并且两端都在圆上的线段。
☆ 圆内最长的线段。
☆ 在同圆或等圆中,直径是半径2倍。
☆ 圆有无数条对称轴(直径所在的直线)。
3. 圆周率(祖冲之,π≈3.14,无限不循环小数)。
(1)圆的周长÷圆的直径=π【C : d=π : 1】
(2)C=πd 逆公式 d=C÷d
=2πr r=C÷d÷2
考点一:圆与各部分之间的关系
圆心(O) 用圆规画圆时,针尖所在的位置
半径(r) 连接圆心和圆上任意一点的线段
半径的长度就是圆规两脚之间的距离
直径(d) 通过圆心并且两端都在圆上的线段
圆周率(π) 任意一个圆的周长与它的直径的比值
它是一个无限不循环小数
考点一:圆与各部分之间的关系
◆ 与圆相关的公式&原理
d=2r
C=πd=2πr
S=πr2
S环=π(R2-r2)
r1:r2=d1:d2=C1:C2
半径、直径、周长扩大的倍数相同面积扩大倍数的平方倍。
面积比需要平方
【某区真题】填空题。
1. 若圆的半径扩大3倍,那么直径扩大( )倍,周长扩大( )倍,面积
扩大( )倍。
3
3
9
2. 小圆半径是大圆半径的 ,那么小圆直径是大圆直径的 ,小圆周长
是大圆周长的 ,小圆面积是大圆面积的 。
3
4
3
4
9
16
考点二
长方形/正方形里剪最大的圆
考点二:长方形/正方形里剪最大的圆
长方形:短边就是圆的直径
正方形:边长就是圆的直径
在一个边长为4分米的正方形里剪下一个最大的圆,这个圆的周长是( )分米,面积是( )平方分米。
12.56
12.56
d=4,r=2
【某区真题】填空题
1. 如下图,在长方形中有三个大小相等的圆,已知这个长方形的长是6厘米,一个圆的直径是( )厘米,长方形的周长是( )厘米。
2. 在一个周长是48厘米的正方形纸片内剪一个最大的圆,圆的半径( )厘米。
2
16
6
考点二:长方形/正方形里剪最大的圆
外方内圆
S正:S圆=
外圆内方
S正:S圆=
1
1
2
4:π
2:π
【某区真题】填空题
1. 如右图,在一个边长为10厘米的正方形纸片中剪下一个最大的圆,这个圆的
面积是( )平方厘米,剩下部分的面积是( )平方厘米,圆的
面积与正方形纸片的面积比是( )。
直径:10cm
半径:5cm
78.5
21.5
π : 4
【某区真题】填空题
2. 已知圆内最大的正方形的面积是30平方厘米,这个圆的面积是( )
平方厘米。
一份面积:30÷2=15 cm
圆:15×3.14=47.1 cm
47.1
考点三
等周长变形
考点三:等周长变形
识记:周长相等的长方形、正方形和圆,S圆>S正>S长
12.56÷4=3.14(厘米)
C=πd
=3.14×4
=12.56(厘米)
一根铁丝刚好能围成一个直径是4厘米的圆,若把它围成一个正方形,正方形的边长是( )厘米。
考点四
半圆的周长和面积
考点四:半圆的周长和面积
C半圆=πd÷2+d
=πr + 2r
=5.14r
【注意是否有靠墙的情况,靠墙时不用加d】
S半圆=πr ÷2
·
·
r
r
S圆=πr
C圆=πd
=2πr
圆周长的一半(πr)
1. 求图中半圆的周长与面积。(单位:厘米)
C半=πd÷2+d
=πr+2r
S半=πr2÷2
C半=3.14×3+2×3
=15.42(厘米)
S半=3.14×32÷2
=14.13(平方厘米)
【某区真题】
【某区真题】
2. 靠墙用篱笆围一个半圆形的菜地,菜地的直径是3米,需要多少米的篱笆?
3.14×3÷2=4.71(米)
答:需要4.71米。
【某区真题】
3. 一个半圆形花坛,周长是10.28米。这个花坛的面积是多少平方米?
r: 10.28÷(3.14+2)=2(米)
3.14×2 ÷2=6.28(平方米)
答:这个花坛的面积是6.28平方米。
考点五
求阴影部分的面积
考点四:求阴影部分的面积
1. 求组合图形的周长常用方法:
☆描边法:曲线部分(圆的周长×几分之几)+线段部分
2. 求组合图形的面积常用方法:
①直接计算;
②小+小;
③大-小。
☆ 六大基本图形的面积计算:
①S长=ab; ④S三=ah÷2;
②S正=a ; ⑤S梯=(a+b)h÷2;
③S平=ah; ⑥S圆=πr
考点四:求阴影部分的面积
4. 扇形的周长和面积
① 先找出圆心角以及圆心角占整个圆的几分之几;
② 算出整个圆的周长或面积,再求它的几分之几是多少。
3. 一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
圆心角:顶点在圆心的角叫圆心角。
☆半径和圆心角决定扇形的大小;
圆心角相等,半径越长,扇形面积越大。
n°
【某区真题】
S长:8×(8÷2)=32(cm2)
r=3cm,R=3+2=5cm
1. 求阴影部分面积。
S环=π(R2-r2)
=3.14×(32-22)
=50.24(cm2)
S半:3.14×(8÷2)2÷2=25.12(cm2)
S阴:32-25.12=6.88(cm2)
【某区真题】
2. 求下图阴影部分的面积。
3.14×8 × =150.72(平方厘米)
S半圆: 3.14×(8÷2)2÷2
=50.24÷2
=25.12(平方厘米)
S梯形:(10+12)×8÷2=88(平方厘米)
88-25.12=62.88(平方厘米)
考点六
解决问题
考点六:解决问题
1. 车轮问题。
(1)车轮滚动一周的长度,就是这个车轮的周长。(C=πd=2πr)
(2)速度:周长×每分钟转的圈数。
(3)路程÷速度=时间【单位统一】
2. 时钟问题【针的长度=半径】:
(1)分针走一圈,1小时; (2) 时针走一圈,12小时;一昼夜=24小时。
① 先算一圈(C=2πr) ① 先算一圈(C=2πr)
② 周长×小时数(或“×分钟÷60“) ② 周长×小时数÷12
【某区真题】
1. 一辆自行车轮胎的外直径是0.7m,如果车轮平均每分钟转100周。4分钟后自行车行进了多少米?
3.14×0.7=2.198(米)
2.198×100×4=879.2(米)
答:4分钟后自行车行进了879.2米。
【某区真题】
2. 一个运动场(如图),两端是半圆形,中间是长方形。
(1)沿着这个运动场跑1圈,要跑多少米?
(2)给这个运动场铺上草坪,一共要铺草坪多少平方米?
(1)3.14×60+100×2=388.4(米)
答:沿着这个运动场跑1圈,要跑388.4米。
(2)3.14×(60÷2) +100×60=8826(平方米)
答:给这个运动场铺上草坪,一共要铺草坪8826平方米。
【某区真题】
3. 时钟的分针长20cm,经过2小时,这跟分针的针尖走了多少厘米?扫过地面积是多少平方厘米?
2×3.14×20×2=251.2(厘米)
3.14×202×2=2512(平方厘米)
答:分针的针尖走了251.2厘米,扫过地面积是2512平方厘米。
感谢观看
