人教B版(2019) 选择性必修第一册 1.1.1 空间向量及其运算 同步练习(Word含答案)
文档属性
| 名称 | 人教B版(2019) 选择性必修第一册 1.1.1 空间向量及其运算 同步练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 166.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 11:06:14 | ||
图片预览




文档简介
第一章 空间向量与立体几何
1.1 空间向量及其运算
1.1.1 空间向量及其运算
基础过关练
题组一 空间向量概念的理解
1.如图,在长方体ABCD-A'B'C'D'中,下列说法正确的是( )
A.=
B.||=||
C.向量与共线
D.向量与共面
2.下列关于空间向量的命题中,正确的个数是( )
①在同一条直线上的单位向量都相等;②只有零向量的模等于0;③在正方体ABCD-A1B1C1D1中,与是相等向量;④在空间四边形ABCD中,与是相反向量;⑤在三棱柱ABC-A1B1C1中,与的模一定相等的向量一共有3个.
A.2 B.3
C.4 D.5
3.(2020辽宁东北育才中学月考)给出下列命题:①若将空间中所有单位向量的起点移到同一个点,则它们的终点构成一个圆;②若空间向量a,b满足|a|=|b|,则a=b;③若空间向量m,n,p满足m=n,n=p,则m=p;④空间中任意两个单位向量必相等;⑤零向量没有方向.其中真命题为 (填序号).
题组二 空间向量的线性运算
4.(多选)(2020山东聊城模拟)已知正方体ABCD-A1B1C1D1,则下列各式运算结果是的为( )
A.++ B.++
C.++ D.++
5.(2021福建厦门海沧实验中学期中)如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若=a,=b,=c,则=( )
A.-a+b+c B.a+b+c
C.a-b+c D.-a-b+c
6.(2021江苏南京期中)在平行六面体ABCD-A1B1C1D1中,=a,=b,=c,点P在A1C上,且A1P∶PC=2∶3,则=( )
A.a+b+c B.a+b+c
C.-a+b+c D.a-b-c
7.化简:(a+2b-3c)+5-3(a-2b-c)= .
8.如图,在正六棱柱ABCDEF-A1B1C1D1E1F1中:(1)化简--+++,并在图中标出化简结果对应的向量;
(2)化简++++,并在图中标出化简结果对应的向量.
9.如图,在长方体ABCD-A1B1C1D1中,O为AC的中点.
(1)化简:--;
(2)设E是棱DD1上的点,且=,若=x+y+z,试求实数x,y,z的值.
题组三 空间向量的数量积
10.(2022河北石家庄一中期末)在空间四边形ABCD中,·+·+·=( )
A.-1 B.0
C.1 D.不确定
11.(2020河南郑州外国语学校模拟)如图,空间四边形ABCD的每条边和对角线长都等于1,F,G分别是AD,CD的中点,则·=( )
A. B. C. D.
12.(2020吉林一中阶段测试)在平行六面体ABCD-A1B1C1D1中,向量,,两两的夹角均为60°,且||=1,||=2,||=3,则||等于( )
A.5 B.6
C.4 D.8
13.(2022北京理工大附中开学考试)已知空间向量a,b,若|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为( )
A.30° B.60°
C.120° D.150°
14.(2020山西大同高级中学模拟)在长方体ABCD-A1B1C1D1中,下列计算结果一定不等于0的是( )
A.· B.·
C.· D.·
能力提升练
题组一 空间向量的线性运算
1.在空间四边形ABCD中,连接AC,BD,若△BCD是正三角形,且E为其重心,则+--的化简结果是( )
A. B.2
C.0 D.2
2.在正三棱柱ABC-A1B1C1中, M为△A1B1C1的重心,若=a,=b,=c,则= .
题组二 空间向量的数量积
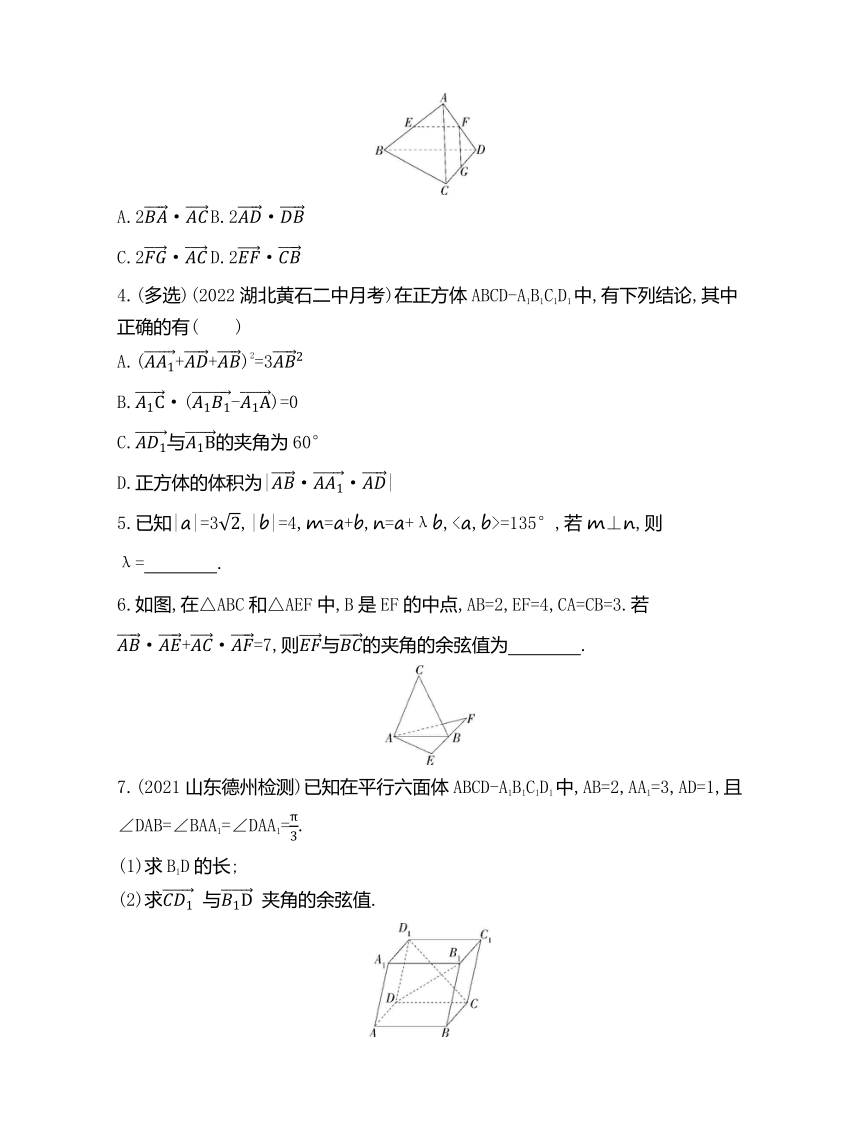
3.(2020江西宜春期末)如图,空间四边形ABCD的每条边和对角线的长都为a,E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是 ( )
A.2· B.2·
C.2· D.2·
4.(多选)(2022湖北黄石二中月考)在正方体ABCD-A1B1C1D1中,有下列结论,其中正确的有( )
A.(++)2=3
B.·(-)=0
C.与的夹角为60°
D.正方体的体积为|··|
5.已知|a|=3,|b|=4,m=a+b,n=a+λb,=135°,若m⊥n,则λ= .
6.如图,在△ABC和△AEF中,B是EF的中点,AB=2,EF=4,CA=CB=3.若·+·=7,则与的夹角的余弦值为 .
7.(2021山东德州检测)已知在平行六面体ABCD-A1B1C1D1中,AB=2,AA1=3,AD=1,且∠DAB=∠BAA1=∠DAA1=.
(1)求B1D的长;
(2)求 与 夹角的余弦值.
答案与分层梯度式解析
第一章 空间向量与立体几何
1.1 空间向量及其运算
1.1.1 空间向量及其运算
基础过关练
1.D 与长度相等,方向相反,故=-,A错误;无法确定||,||的大小,故B错误;与不是共线向量,但可以平移到同一平面上,是共面向量,故C错误,D正确.
2.A ①错误,在同一条直线上的单位向量,方向可能相同,也可能相反,故它们不一定相等;②正确,零向量的模等于0,模等于0的向量只有零向量;③正确,与的模相等,方向相同;④错误,空间四边形ABCD中,与的模不一定相等,方向一定不相反;⑤错误,在三棱柱ABC-A1B1C1中,与的模一定相等的向量有,,,,,共5个.故选A.
3.答案 ③
解析 ①假命题.若将空间中所有单位向量的起点移到同一个点,则它们的终点将构成一个球面,而不是一个圆.②假命题.根据向量相等的定义,要保证两个向量相等,不仅模要相等,而且方向还要相同,但②中向量a与b的方向不一定相同.③真命题.向量的相等具有传递性.④假命题.空间中任意两个单位向量的模均为1,但方向不一定相同,所以不一定相等.⑤假命题.零向量的方向是任意的.
4.ABC 选项A中,++=+=;
选项B中,++=+(+)=+=;
选项C中,++=+=;
选项D中,++=+(+)=+≠.故选ABC.
5.A =++=++
=++(+)=-a+c+(a+b)
=-a+b+c.
6.
B 如图,因为A1P∶PC=2∶3,所以=,所以=+=+=+(-)=+=+(+)=++,又=a,=b,=c,所以=a+b+c.故选B.
7.答案 a+b+c
解析 原式=a+b+×(-3)+5×-3×(-1)c=a+b+c.
8.解析 (1)--+++=+++++=++0=+=.
如图所示.
(2)++++=++++=++=0+=.
如图所示.
9.解析 (1)∵+=,
∴--=-(+)=-=-=.
(2)∵=+=+=+(+)=++=--,
∴x=,y=-,z=-.
10.B 令=a,=b,=c,则·+·+·=a·(c-b)+b·(a-c)+c·(b-a)=a·c-a·b+b·a-b·c+c·b-c·a=0.
11.B 由题意得=,所以·=·=×1×1×cos 60°=.故选B.
12.A ||2=(++)2=||2+||2+||2+2·+2·+2·=1+4+9+2+3+6=25,∴||=5,故选A.
13.C 设向量a与b的夹角为θ.∵c⊥a,∴c·a=(a+b)·a=0,则|a|2+|a||b|cos θ=0,∴cos θ=-,∴θ=120°.
14.D 如图所示:
对于A,当长方体为正方体时,AD1⊥B1C,此时·=0,故选项A不符合;
对于B,当长方体的底面ABCD是正方形时,AC⊥BD,可以推出AC⊥平面BB1D1D,则BD1⊥AC,此时·=0,故选项B不符合;
对于C,易知DC⊥AD1,所以·=0,故选项C不符合;
对于D,因为B1C1∥A1D1,BD1与A1D1分别是直角三角形BA1D1的斜边和直角边,二者不可能垂直,所以B1C1与BD1不可能垂直,所以·≠0.故选D.
解题指导 判断两个向量的数量积的结果与0的关系可转化为应用立体几何中相关定理判断两直线是否垂直的问题.
能力提升练
1.C 如图所示,取BC的中点F,则=,又E为正三角形BCD的重心,即DF上靠近F的三等分点,所以=,则+--=+--=+-=-=0.
2.答案 c+-
解析 如图,连接C1M并延长,交A1B1于点D.
∵在正三棱柱ABC-A1B1C1中,M为△A1B1C1的重心,=a,=b,=c,∴=+=c+=c+×(+)=c+(-b+-)=c+(-b+a-b)=c+-.
3.C 由题意可知,<,>=<,>=<,>=120°,∴2·=2||||cos 120°=-a2,2·=2||||cos 120°=-a2.∵E,F,G分别是AB,AD,DC的中点,∴FG∥AC且FG=AC,EF∥BD且EF=BD,∴2·==a2,2·=·=||||cos 120°=-a2.故选C.
4.AB (++)2=(++)2==3,故A正确;
·(-)=·=(+)·=·+·=0,故B正确;
与的夹角是与夹角的补角,而△ACD1为正三角形,所以与的夹角为60°,故与的夹角是120°,故C错误;
正方体的体积为||||||,故D错误.
5.答案 -
解析 ∵|a|=3,|b|=4,m=a+b,n=a+λb,=135°,∴m·n=(a+b)·(a+λb)=a2+(λ+1)a·b+λb2=(3)2+(λ+1)×3×4cos 135°+λ×42=0,即4λ+6=0,解得λ=-.
6.答案
解析 由题意得=9=(-)2=+-2·=9+4-2·,所以·=2.由·+·=7,可得·(+)+·(+)=+·+·+·=4+·(-)+2+·=6+·(-)=6+·=7.所以·=2,即4×3×cos<,>=2,所以cos<,>=.
7.解析 (1)由题可知,=++=--,则||==
==,
因此,B1D的长为.
(2)由题知,==-,
则||=
=
==,
∴·=(-)·(--)
=·-·--·++·
=·--·+
=3×1×-32-2×1×+22=-,
∴cos<,>===-.
1.1 空间向量及其运算
1.1.1 空间向量及其运算
基础过关练
题组一 空间向量概念的理解
1.如图,在长方体ABCD-A'B'C'D'中,下列说法正确的是( )
A.=
B.||=||
C.向量与共线
D.向量与共面
2.下列关于空间向量的命题中,正确的个数是( )
①在同一条直线上的单位向量都相等;②只有零向量的模等于0;③在正方体ABCD-A1B1C1D1中,与是相等向量;④在空间四边形ABCD中,与是相反向量;⑤在三棱柱ABC-A1B1C1中,与的模一定相等的向量一共有3个.
A.2 B.3
C.4 D.5
3.(2020辽宁东北育才中学月考)给出下列命题:①若将空间中所有单位向量的起点移到同一个点,则它们的终点构成一个圆;②若空间向量a,b满足|a|=|b|,则a=b;③若空间向量m,n,p满足m=n,n=p,则m=p;④空间中任意两个单位向量必相等;⑤零向量没有方向.其中真命题为 (填序号).
题组二 空间向量的线性运算
4.(多选)(2020山东聊城模拟)已知正方体ABCD-A1B1C1D1,则下列各式运算结果是的为( )
A.++ B.++
C.++ D.++
5.(2021福建厦门海沧实验中学期中)如图,在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若=a,=b,=c,则=( )
A.-a+b+c B.a+b+c
C.a-b+c D.-a-b+c
6.(2021江苏南京期中)在平行六面体ABCD-A1B1C1D1中,=a,=b,=c,点P在A1C上,且A1P∶PC=2∶3,则=( )
A.a+b+c B.a+b+c
C.-a+b+c D.a-b-c
7.化简:(a+2b-3c)+5-3(a-2b-c)= .
8.如图,在正六棱柱ABCDEF-A1B1C1D1E1F1中:(1)化简--+++,并在图中标出化简结果对应的向量;
(2)化简++++,并在图中标出化简结果对应的向量.
9.如图,在长方体ABCD-A1B1C1D1中,O为AC的中点.
(1)化简:--;
(2)设E是棱DD1上的点,且=,若=x+y+z,试求实数x,y,z的值.
题组三 空间向量的数量积
10.(2022河北石家庄一中期末)在空间四边形ABCD中,·+·+·=( )
A.-1 B.0
C.1 D.不确定
11.(2020河南郑州外国语学校模拟)如图,空间四边形ABCD的每条边和对角线长都等于1,F,G分别是AD,CD的中点,则·=( )
A. B. C. D.
12.(2020吉林一中阶段测试)在平行六面体ABCD-A1B1C1D1中,向量,,两两的夹角均为60°,且||=1,||=2,||=3,则||等于( )
A.5 B.6
C.4 D.8
13.(2022北京理工大附中开学考试)已知空间向量a,b,若|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为( )
A.30° B.60°
C.120° D.150°
14.(2020山西大同高级中学模拟)在长方体ABCD-A1B1C1D1中,下列计算结果一定不等于0的是( )
A.· B.·
C.· D.·
能力提升练
题组一 空间向量的线性运算
1.在空间四边形ABCD中,连接AC,BD,若△BCD是正三角形,且E为其重心,则+--的化简结果是( )
A. B.2
C.0 D.2
2.在正三棱柱ABC-A1B1C1中, M为△A1B1C1的重心,若=a,=b,=c,则= .
题组二 空间向量的数量积
3.(2020江西宜春期末)如图,空间四边形ABCD的每条边和对角线的长都为a,E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是 ( )
A.2· B.2·
C.2· D.2·
4.(多选)(2022湖北黄石二中月考)在正方体ABCD-A1B1C1D1中,有下列结论,其中正确的有( )
A.(++)2=3
B.·(-)=0
C.与的夹角为60°
D.正方体的体积为|··|
5.已知|a|=3,|b|=4,m=a+b,n=a+λb,
6.如图,在△ABC和△AEF中,B是EF的中点,AB=2,EF=4,CA=CB=3.若·+·=7,则与的夹角的余弦值为 .
7.(2021山东德州检测)已知在平行六面体ABCD-A1B1C1D1中,AB=2,AA1=3,AD=1,且∠DAB=∠BAA1=∠DAA1=.
(1)求B1D的长;
(2)求 与 夹角的余弦值.
答案与分层梯度式解析
第一章 空间向量与立体几何
1.1 空间向量及其运算
1.1.1 空间向量及其运算
基础过关练
1.D 与长度相等,方向相反,故=-,A错误;无法确定||,||的大小,故B错误;与不是共线向量,但可以平移到同一平面上,是共面向量,故C错误,D正确.
2.A ①错误,在同一条直线上的单位向量,方向可能相同,也可能相反,故它们不一定相等;②正确,零向量的模等于0,模等于0的向量只有零向量;③正确,与的模相等,方向相同;④错误,空间四边形ABCD中,与的模不一定相等,方向一定不相反;⑤错误,在三棱柱ABC-A1B1C1中,与的模一定相等的向量有,,,,,共5个.故选A.
3.答案 ③
解析 ①假命题.若将空间中所有单位向量的起点移到同一个点,则它们的终点将构成一个球面,而不是一个圆.②假命题.根据向量相等的定义,要保证两个向量相等,不仅模要相等,而且方向还要相同,但②中向量a与b的方向不一定相同.③真命题.向量的相等具有传递性.④假命题.空间中任意两个单位向量的模均为1,但方向不一定相同,所以不一定相等.⑤假命题.零向量的方向是任意的.
4.ABC 选项A中,++=+=;
选项B中,++=+(+)=+=;
选项C中,++=+=;
选项D中,++=+(+)=+≠.故选ABC.
5.A =++=++
=++(+)=-a+c+(a+b)
=-a+b+c.
6.
B 如图,因为A1P∶PC=2∶3,所以=,所以=+=+=+(-)=+=+(+)=++,又=a,=b,=c,所以=a+b+c.故选B.
7.答案 a+b+c
解析 原式=a+b+×(-3)+5×-3×(-1)c=a+b+c.
8.解析 (1)--+++=+++++=++0=+=.
如图所示.
(2)++++=++++=++=0+=.
如图所示.
9.解析 (1)∵+=,
∴--=-(+)=-=-=.
(2)∵=+=+=+(+)=++=--,
∴x=,y=-,z=-.
10.B 令=a,=b,=c,则·+·+·=a·(c-b)+b·(a-c)+c·(b-a)=a·c-a·b+b·a-b·c+c·b-c·a=0.
11.B 由题意得=,所以·=·=×1×1×cos 60°=.故选B.
12.A ||2=(++)2=||2+||2+||2+2·+2·+2·=1+4+9+2+3+6=25,∴||=5,故选A.
13.C 设向量a与b的夹角为θ.∵c⊥a,∴c·a=(a+b)·a=0,则|a|2+|a||b|cos θ=0,∴cos θ=-,∴θ=120°.
14.D 如图所示:
对于A,当长方体为正方体时,AD1⊥B1C,此时·=0,故选项A不符合;
对于B,当长方体的底面ABCD是正方形时,AC⊥BD,可以推出AC⊥平面BB1D1D,则BD1⊥AC,此时·=0,故选项B不符合;
对于C,易知DC⊥AD1,所以·=0,故选项C不符合;
对于D,因为B1C1∥A1D1,BD1与A1D1分别是直角三角形BA1D1的斜边和直角边,二者不可能垂直,所以B1C1与BD1不可能垂直,所以·≠0.故选D.
解题指导 判断两个向量的数量积的结果与0的关系可转化为应用立体几何中相关定理判断两直线是否垂直的问题.
能力提升练
1.C 如图所示,取BC的中点F,则=,又E为正三角形BCD的重心,即DF上靠近F的三等分点,所以=,则+--=+--=+-=-=0.
2.答案 c+-
解析 如图,连接C1M并延长,交A1B1于点D.
∵在正三棱柱ABC-A1B1C1中,M为△A1B1C1的重心,=a,=b,=c,∴=+=c+=c+×(+)=c+(-b+-)=c+(-b+a-b)=c+-.
3.C 由题意可知,<,>=<,>=<,>=120°,∴2·=2||||cos 120°=-a2,2·=2||||cos 120°=-a2.∵E,F,G分别是AB,AD,DC的中点,∴FG∥AC且FG=AC,EF∥BD且EF=BD,∴2·==a2,2·=·=||||cos 120°=-a2.故选C.
4.AB (++)2=(++)2==3,故A正确;
·(-)=·=(+)·=·+·=0,故B正确;
与的夹角是与夹角的补角,而△ACD1为正三角形,所以与的夹角为60°,故与的夹角是120°,故C错误;
正方体的体积为||||||,故D错误.
5.答案 -
解析 ∵|a|=3,|b|=4,m=a+b,n=a+λb,
6.答案
解析 由题意得=9=(-)2=+-2·=9+4-2·,所以·=2.由·+·=7,可得·(+)+·(+)=+·+·+·=4+·(-)+2+·=6+·(-)=6+·=7.所以·=2,即4×3×cos<,>=2,所以cos<,>=.
7.解析 (1)由题可知,=++=--,则||==
==,
因此,B1D的长为.
(2)由题知,==-,
则||=
=
==,
∴·=(-)·(--)
=·-·--·++·
=·--·+
=3×1×-32-2×1×+22=-,
∴cos<,>===-.
