人教B版(2019)选择性必修第一册 1.2.3 直线与平面的夹角 同步练习(Word含答案)
文档属性
| 名称 | 人教B版(2019)选择性必修第一册 1.2.3 直线与平面的夹角 同步练习(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 294.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 11:17:40 | ||
图片预览



文档简介
第一章 空间向量与立体几何
1.2 空间向量在立体几何中的应用
1.2.3 直线与平面的夹角
基础过关练
题组一 用定义研究线面角问题
1.(2020河南濮阳油田一中调研)在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱B1B的中点,则直线AE与平面A1ED1所成角的大小是( )
A.60° B.90°
C.45° D.以上都不对
2.(2022山西运城模拟)某正四棱锥的侧棱与底面所成的角为45°,则该正四棱锥的一个侧面与底面的面积之比为( )
A. B. C. D.
3.(2020四川成都期末)将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦值为( )
A. B.
C. D.
题组二 公式cos θ=cos θ1cos θ2的应用
4.已知平面α内的∠APB=60°,射线PC与PA,PB所成的角均为135°,则PC与平面α所成的角θ的余弦值是( )
A.- B. C. D.-
5.若BC在平面α内,斜线AB与平面α所成的角为γ,∠ABC=θ,AA'⊥平面α,垂足为A',∠A'BC=β,θ,γ∈,那么( )
A.cos θ=cos γ·cos β
B.sin θ=sin γ·sin β
C.cos γ=cos θ·cos β
D.cos β=cos γ·cos θ
题组三 用向量法研究线面角问题
6.(2021吉林通化综合高级中学期末)若平面α的一个法向量为n=(2,1,1),直线l的一个方向向量为a=(1,2,3),则直线l与平面α所成角的正弦值为( )
A. B. C.- D.
7.(2022福建厦门集美中学检测)在直三棱柱ABC-A1B1C1中,△ABC为等边三角形,AA1=AB,M是A1C1的中点,则直线AM与平面BCC1B1所成角的正弦值为( )
A. B. C. D.-
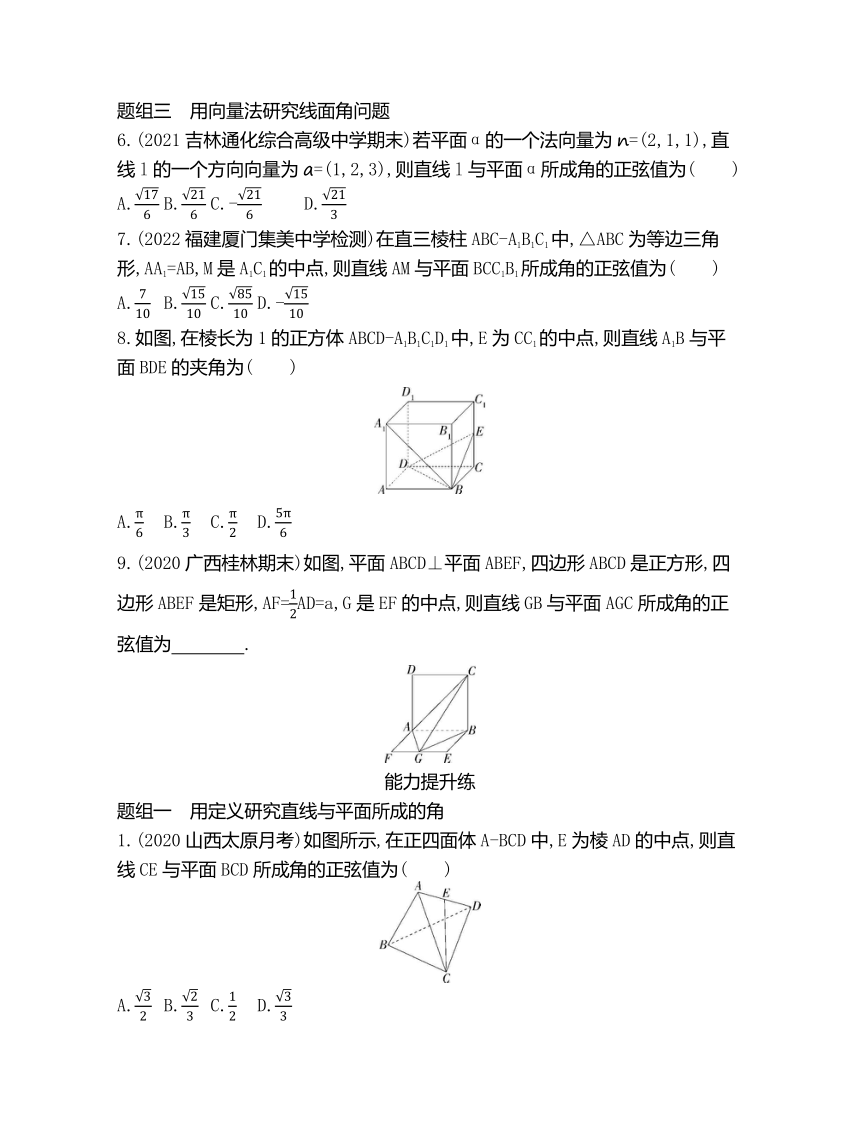
8.如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线A1B与平面BDE的夹角为( )
A. B. C. D.
9.(2020广西桂林期末)如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,AF=AD=a,G是EF的中点,则直线GB与平面AGC所成角的正弦值为 .
能力提升练
题组一 用定义研究直线与平面所成的角
1.(2020山西太原月考)如图所示,在正四面体A-BCD中,E为棱AD的中点,则直线CE与平面BCD所成角的正弦值为( )
A. B. C. D.
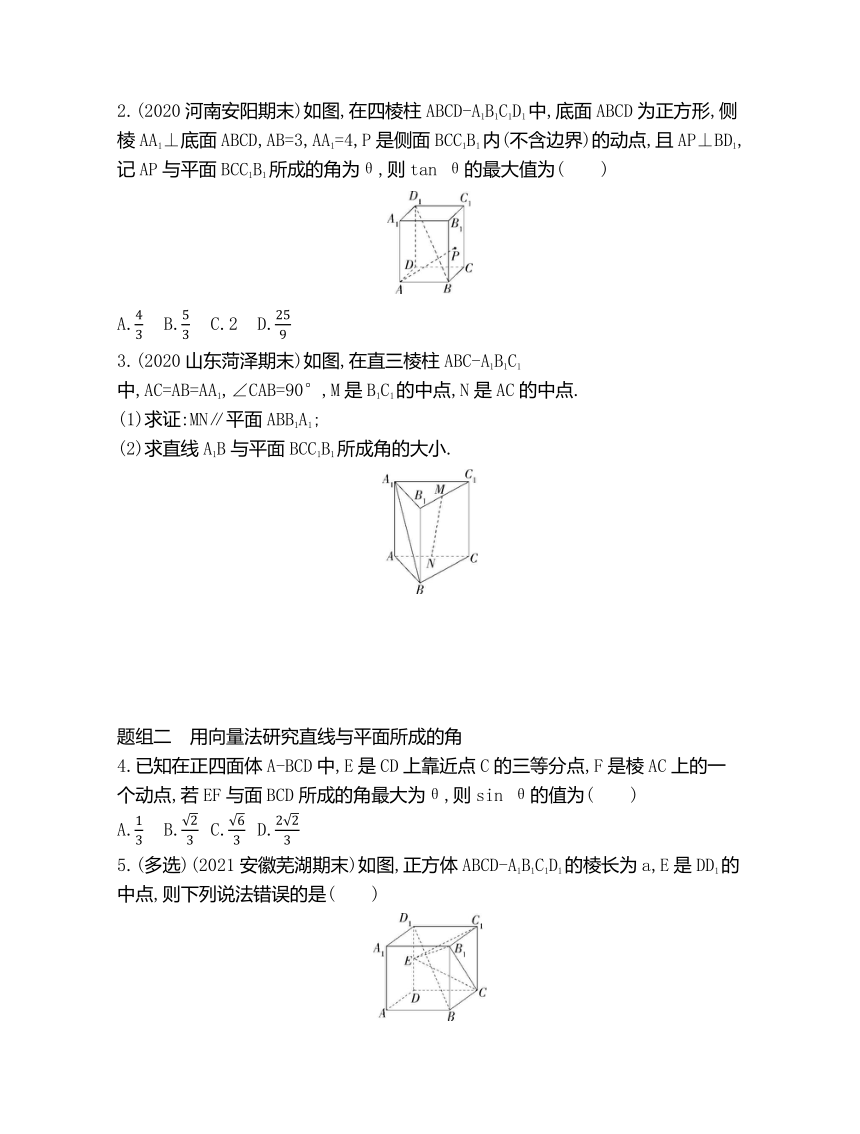
2.(2020河南安阳期末)如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,侧棱AA1⊥底面ABCD,AB=3,AA1=4,P是侧面BCC1B1内(不含边界)的动点,且AP⊥BD1,记AP与平面BCC1B1所成的角为θ,则tan θ的最大值为( )
A. B. C.2 D.
3.(2020山东菏泽期末)如图,在直三棱柱ABC-A1B1C1中,AC=AB=AA1,∠CAB=90°,M是B1C1的中点,N是AC的中点.
(1)求证:MN∥平面ABB1A1;
(2)求直线A1B与平面BCC1B1所成角的大小.
题组二 用向量法研究直线与平面所成的角
4.已知在正四面体A-BCD中,E是CD上靠近点C的三等分点,F是棱AC上的一个动点,若EF与面BCD所成的角最大为θ,则sin θ的值为( )
A. B. C. D.
5.(多选)(2021安徽芜湖期末)如图,正方体ABCD-A1B1C1D1的棱长为a,E是DD1的中点,则下列说法错误的是( )
A.直线B1E∥平面A1BD
B.B1E⊥BD1
C.三棱锥C1-B1CE的体积为a3
D.直线B1E与平面CDD1C1所成角的正切值为
6.(2020黑龙江牡丹江第一中学期末)如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,点P在线段A1C1上,若直线OP与平面A1BC1所成的角为θ,则sin θ的取值范围是( )
A. B.
C. D.
7.(2020上海七宝中学期末)如图,点O为正四棱锥P-ABCD的底面ABCD的中心,四边形POBQ为矩形,且OA=,BQ=2.
(1)求正四棱锥P-ABCD的体积;
(2)设E为侧棱PA上的点,且=,求直线BE与平面PQC所成角的大小.
8.(2020江苏徐州月考)如图,在四棱锥E-ABCD中,底面ABCD是圆内接四边形,CB=CD=CE=1,AB=AD=AE=,EC⊥BD.
(1)求证:平面BED⊥平面ABCD;
(2)若点P在侧面ABE内运动,且DP∥平面BEC,求直线DP与平面ABE所成角的正弦值的最大值.
9.(2020山东枣庄期中)如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,AD=1,PA=AB=BC=2,M是棱PB的中点.
(1)已知点E在棱BC上,且平面AME∥平面PCD,试确定点E的位置并说明理由;
(2)设N是线段CD上的动点,当点N在何处时,直线MN与平面PAB所成的角最大 并求最大角的正弦值.
答案与分层梯度式解析
第一章 空间向量与立体几何
1.2 空间向量在立体几何中的应用
1.2.3 直线与平面的夹角
基础过关练
1.B 由题意可知AE=A1E=,则AE2+A1E2=A,故AE⊥A1E.在长方体ABCD-A1B1C1D1中,A1D1⊥平面ABB1A1.又AE 平面ABB1A1,所以A1D1⊥AE.因为A1D1∩A1E=A1,所以AE⊥平面A1ED1,所以∠AEA1是直线AE与平面A1ED1所成的角,其大小为90°.故选B.
方法点拨 作直线与平面夹角的一般方法:在直线上找一点,通过这个点作平面的垂线,从而确定射影,找到要求的角.其中的关键是作平面的垂线,此方法简称为“一作,二证,三计算”.
2.D 如图,PO是正四棱锥P-ABCD的高,
设底面边长为a,则底面积S1=a2.
因为正四棱锥的侧棱与底面所成的角为45°,
所以∠PAO=45°,
又AO=a,所以PA=×a=a,
所以△PAB是正三角形,所以侧面PAB的面积S2=a2,所以==.
3.C 过点E作EF⊥BD,垂足为F,连接AF,则∠EAF即为直线AE与平面ABD所成的角,不妨设正方形的边长为2,则BF=EF=,AB=2,在△ABF中,由余弦定理可得AF2=AB2+BF2-2AB·BF·cos∠ABF=,所以AF=,在Rt△AEF中,AE2=AF2+EF2=3,所以AE=,故cos∠EAF==.
4.B 由题可知cos 45°=cos θ·cos 30°,∴cos θ=.
5.A 由公式cos θ=cos θ1cos θ2可知A正确.
6.B 因为平面α的一个法向量为n=(2,1,1),直线l的一个方向向量为a=(1,2,3),
所以直线l与平面α所成角的正弦值为|cos|==.
7.B 如图所示,取AC的中点D,以D为原点,BD,DC,DM所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
不妨设AC=2,则A(0,-1,0),M(0,0,2),B(-,0,0),C(0,1,0),B1(-,0,2),
所以=(0,1,2),=(,1,0),=(0,0,2).
设平面BCC1B1的一个法向量为n=(x,y,z),则令x=,则y=-3,z=0,所以n=(,-3,0).
设直线AM与平面BCC1B1所成的角为α,
则sin α=|cos <,n>|==,
即直线AM与平面BCC1B1所成角的正弦值为.
8.B 以D为原点,,,的方向分别为x轴、y轴、z轴的正方向建立如图所示的空间直角坐标系,
则D(0,0,0),A(1,0,0),B(1,1,0),E,A1(1,0,1),∴=(1,1,0),=.设平面BDE的一个法向量为n=(x,y,z),则即令x=1,则y=-1,z=2,∴平面BDE的一个法向量为n=(1,-1,2).∵=(0,-1,1),∴cos<,n>==,又∵<,n>∈[0,π],∴<,n>=,∴直线A1B与平面BDE的夹角为.故选B.
9.答案
解析 由于平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,故AF,AB,AD两两互相垂直,以A为原点,,,的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系,如图所示,
则A(0,0,0),G(a,a,0),B(0,2a,0),C(0,2a,2a),所以=(-a,a,0),=(0,2a,2a),=(a,a,0),
设平面AGC的一个法向量为n=(x,y,z),
则
令x=1,得n=(1,-1,1),
因此直线GB与平面AGC所成角的正弦值为|cos|===.
能力提升练
1.B 在正四面体A-BCD中,E为棱AD的中点,设棱长为a,如图所示,过点A作AO⊥平面BCD,垂足为O,则点O为△BCD的中心,连接DO并延长,交BC于点G,过点E作EF⊥GD于点F,连接FC,则∠ECF即为直线CE与平面BCD所成的角.由GD2=CD2-CG2,得GD=a,所以OD=GD=a.由AO2=AD2-OD2,得AO=a,所以EF=AO=a.又CE=GD=a,所以在Rt△EFC中,sin∠ECF==.故选B.
2.B 连接PB.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则A(3,0,0),B(3,3,0),D1(0,0,4).设P(x,3,z),03.解析 (1)证明:如图,取AB的中点H,连接HN,B1H,则HN是△ABC的中位线,
所以HN∥BC,且HN=BC,
又因为B1M∥BC,且B1M=BC,
所以HN∥B1M,且HN=B1M,
所以四边形HNMB1是平行四边形,
所以MN∥B1H,
又因为MN 平面ABB1A1,B1H 平面ABB1A1,
所以MN∥平面ABB1A1.
(2)连接A1M,BM,因为A1B1=A1C1,M是B1C1的中点,所以A1M⊥B1C1.
又因为面A1B1C1⊥面BCC1B1,A1M 面A1B1C1,面A1B1C1∩面BCC1B1=B1C1,
所以A1M⊥面BCC1B1,
所以直线BM为A1B在面BCC1B1内的射影,
所以∠A1BM为直线A1B与平面BCC1B1所成的角.
设AB=2,则A1M=,A1B=2,
所以sin∠A1BM===,
所以∠A1BM=30°,
所以直线A1B与平面BCC1B1所成角的大小为30°.
4.D 如图所示,将正四面体A-BCD放入一个正方体中,且建立空间直角坐标系,设正方体的棱长为3,则A(0,0,3),B(0,3,0),C(3,0,0),D(3,3,3),E(3,1,1),
所以=(3,-3,0),=(3,0,3),=(0,-1,-1),=(-3,0,3).
设=λ=(-3λ,0,3λ),0≤λ≤1,则=+=(-3λ,-1,3λ-1).
设平面BCD的一个法向量为n=(x,y,z),
则即令x=1,则y=1,z=-1,即n=(1,1,-1),
设EF与平面BCD所成的角为α,则sin α=|cos|==,
当λ=0时,sin α=0,
当0<λ≤1时,sin α=,则当=,即λ=时,sin α取得最大值,此时α最大,则sin θ=(sin α)max=.
5.ABC 如图,建立空间直角坐标系,则A1(a,0,a),B1(a,a,a),E,B(a,a,0),D(0,0,0),D1(0,0,a),则=,=(a,a,0),=(a,0,a),=(-a,-a,a),设平面A1BD的一个法向量为n=(x,y,z),则取x=1,则y=z=-1,所以n=(1,-1,-1),所以n·=1×(-a)+(-1)×(-a)+(-1)×=≠0,故B1E不平行于平面A1BD,故A错误;
因为·=(-a)×(-a)+(-a)×(-a)+a×=a2≠0,所以与不垂直,故B错误;
==·B1C1=a3,故C错误;
易知平面CDD1C1的一个法向量为m=(1,0,0),设直线B1E与平面CDD1C1所成的角为θ,则sin θ===,所以cos θ==,
所以tan θ===,故D正确.
6.A 设正方体的棱长为1,=λ(0≤λ≤1).
以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则D(0,0,0),B1(1,1,1),O,P(1-λ,λ,1),所以=.
连接B1D,在正方体ABCD-A1B1C1D1中,易证得B1D⊥平面A1BC1,所以=(-1,-1,-1)是平面A1BC1的一个法向量,
所以sin θ=|cos<,>|
==,
当λ=时,sin θ取得最大值,
当λ=0或λ=1时,sin θ取得最小值.故sin θ∈.
故选A.
7.解析 (1)由已知可得OP=BQ=2,
因为OA=,所以AB=2,
所以正四棱锥P-ABCD的体积V=×S正方形ABCD×PO=×22×2=.
(2)以O为原点,OC,OD,OP所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,易得P(0,0,2),A(-,0,0),B(0,-,0),C(,0,0),Q(0,-,2),所以=(0,,0),=(-,0,2),=(,0,2).
设平面PQC的一个法向量为n=(x0,y0,z0),则即
令x0=,得n=(,0,1).
依题意可得==,
设E(x,y,z),则=(x+,y,z),
所以(x+,y,z)=,解得
故E,所以=.
设直线BE与平面PQC所成的角为θ,
则sin θ=|cos<,n>|===.
因为θ∈,所以θ=arcsin.
故直线BE与平面PQC所成角的大小为arcsin.
8.解析 (1)证明:如图,连接AC,交BD于点O,连接EO,
易证得△ADC≌△ABC,△ADO≌△ABO,
所以∠AOD=∠AOB=90°,
所以AC垂直平分BD.
又EC⊥BD,EC∩AC=C,所以BD⊥平面AEC,
又EO 平面AEC,所以EO⊥BD,
又底面ABCD是圆内接四边形,
所以∠ADC=∠ABC=90°.
在Rt△ADC中,由AD=,CD=1,可得AC=2,AO=,则AC2=AE2+CE2,所以∠AEC=90°,==,
又因为∠EAO=∠CAE,所以△AEO∽△ACE,
所以∠AOE=∠AEC=90°,即EO⊥AC,
又AC,BD 平面ABCD,AC∩BD=O,
所以EO⊥平面ABCD,
又EO 平面BED,所以平面BED⊥平面ABCD.
(2)如图,取AE的中点M,AB的中点N,连接MN,MD,DN,则MN∥BE,
由(1)易知,∠DAC=∠BAC=30°,即∠DAB=60°,
所以△ABD为正三角形,所以DN⊥AB,
又BC⊥AB,所以DN∥BC,又MN∩DN=N,BE∩BC=B,所以平面DMN∥平面EBC,
所以点P在线段MN上.
以O为坐标原点,建立如图所示的空间直角坐标系,
则A,B,E,
M,D,N,
所以=,=,=,=.
设平面ABE的一个法向量为n=(x,y,z),
则即
令x=1,则n=(1,,).
设=λ(0≤λ≤1),可得
=+=.
设直线DP与平面ABE所成的角为θ,
则sin θ==,
因为0≤λ≤1,所以当λ=0时,sin θ取得最大值.
故直线DP与平面ABE所成角的正弦值的最大值为.
9.解析 (1)E是BC的中点,理由如下:
∵平面AME∥平面PCD,平面ABCD∩平面AME=AE,平面ABCD∩平面PCD=CD,∴AE∥CD,
又∵AD∥EC,∴四边形ADCE是平行四边形,
∴EC=AD=1,
又∵BC=2,∴BE=EC,即E是BC的中点.
(2)由题意知PA,AB,AD两两互相垂直.以A为原点,AD,AB,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则A(0,0,0),B(0,2,0),C(2,2,0),D(1,0,0),P(0,0,2),M(0,1,1),
∴=(0,-1,-1),=(1,0,0),=(1,2,0).
设直线MN与平面PAB所成的角为θ,=λ(0≤λ≤1),则=++=(λ+1,2λ-1,-1).
易知n=(1,0,0)为平面PAB的一个法向量,
则sin θ=|cos<,n>|=
=.
令λ+1=t,则t∈[1,2],
则==,
∴当t=,即λ=时,sin θ取得最大值,为,
∴当N是线段DC上靠近C的三等分点时,直线MN与平面PAB所成的角最大,最大角的正弦值为.
1.2 空间向量在立体几何中的应用
1.2.3 直线与平面的夹角
基础过关练
题组一 用定义研究线面角问题
1.(2020河南濮阳油田一中调研)在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱B1B的中点,则直线AE与平面A1ED1所成角的大小是( )
A.60° B.90°
C.45° D.以上都不对
2.(2022山西运城模拟)某正四棱锥的侧棱与底面所成的角为45°,则该正四棱锥的一个侧面与底面的面积之比为( )
A. B. C. D.
3.(2020四川成都期末)将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦值为( )
A. B.
C. D.
题组二 公式cos θ=cos θ1cos θ2的应用
4.已知平面α内的∠APB=60°,射线PC与PA,PB所成的角均为135°,则PC与平面α所成的角θ的余弦值是( )
A.- B. C. D.-
5.若BC在平面α内,斜线AB与平面α所成的角为γ,∠ABC=θ,AA'⊥平面α,垂足为A',∠A'BC=β,θ,γ∈,那么( )
A.cos θ=cos γ·cos β
B.sin θ=sin γ·sin β
C.cos γ=cos θ·cos β
D.cos β=cos γ·cos θ
题组三 用向量法研究线面角问题
6.(2021吉林通化综合高级中学期末)若平面α的一个法向量为n=(2,1,1),直线l的一个方向向量为a=(1,2,3),则直线l与平面α所成角的正弦值为( )
A. B. C.- D.
7.(2022福建厦门集美中学检测)在直三棱柱ABC-A1B1C1中,△ABC为等边三角形,AA1=AB,M是A1C1的中点,则直线AM与平面BCC1B1所成角的正弦值为( )
A. B. C. D.-
8.如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为CC1的中点,则直线A1B与平面BDE的夹角为( )
A. B. C. D.
9.(2020广西桂林期末)如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,AF=AD=a,G是EF的中点,则直线GB与平面AGC所成角的正弦值为 .
能力提升练
题组一 用定义研究直线与平面所成的角
1.(2020山西太原月考)如图所示,在正四面体A-BCD中,E为棱AD的中点,则直线CE与平面BCD所成角的正弦值为( )
A. B. C. D.
2.(2020河南安阳期末)如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,侧棱AA1⊥底面ABCD,AB=3,AA1=4,P是侧面BCC1B1内(不含边界)的动点,且AP⊥BD1,记AP与平面BCC1B1所成的角为θ,则tan θ的最大值为( )
A. B. C.2 D.
3.(2020山东菏泽期末)如图,在直三棱柱ABC-A1B1C1中,AC=AB=AA1,∠CAB=90°,M是B1C1的中点,N是AC的中点.
(1)求证:MN∥平面ABB1A1;
(2)求直线A1B与平面BCC1B1所成角的大小.
题组二 用向量法研究直线与平面所成的角
4.已知在正四面体A-BCD中,E是CD上靠近点C的三等分点,F是棱AC上的一个动点,若EF与面BCD所成的角最大为θ,则sin θ的值为( )
A. B. C. D.
5.(多选)(2021安徽芜湖期末)如图,正方体ABCD-A1B1C1D1的棱长为a,E是DD1的中点,则下列说法错误的是( )
A.直线B1E∥平面A1BD
B.B1E⊥BD1
C.三棱锥C1-B1CE的体积为a3
D.直线B1E与平面CDD1C1所成角的正切值为
6.(2020黑龙江牡丹江第一中学期末)如图,在正方体ABCD-A1B1C1D1中,O是AC的中点,点P在线段A1C1上,若直线OP与平面A1BC1所成的角为θ,则sin θ的取值范围是( )
A. B.
C. D.
7.(2020上海七宝中学期末)如图,点O为正四棱锥P-ABCD的底面ABCD的中心,四边形POBQ为矩形,且OA=,BQ=2.
(1)求正四棱锥P-ABCD的体积;
(2)设E为侧棱PA上的点,且=,求直线BE与平面PQC所成角的大小.
8.(2020江苏徐州月考)如图,在四棱锥E-ABCD中,底面ABCD是圆内接四边形,CB=CD=CE=1,AB=AD=AE=,EC⊥BD.
(1)求证:平面BED⊥平面ABCD;
(2)若点P在侧面ABE内运动,且DP∥平面BEC,求直线DP与平面ABE所成角的正弦值的最大值.
9.(2020山东枣庄期中)如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,AD=1,PA=AB=BC=2,M是棱PB的中点.
(1)已知点E在棱BC上,且平面AME∥平面PCD,试确定点E的位置并说明理由;
(2)设N是线段CD上的动点,当点N在何处时,直线MN与平面PAB所成的角最大 并求最大角的正弦值.
答案与分层梯度式解析
第一章 空间向量与立体几何
1.2 空间向量在立体几何中的应用
1.2.3 直线与平面的夹角
基础过关练
1.B 由题意可知AE=A1E=,则AE2+A1E2=A,故AE⊥A1E.在长方体ABCD-A1B1C1D1中,A1D1⊥平面ABB1A1.又AE 平面ABB1A1,所以A1D1⊥AE.因为A1D1∩A1E=A1,所以AE⊥平面A1ED1,所以∠AEA1是直线AE与平面A1ED1所成的角,其大小为90°.故选B.
方法点拨 作直线与平面夹角的一般方法:在直线上找一点,通过这个点作平面的垂线,从而确定射影,找到要求的角.其中的关键是作平面的垂线,此方法简称为“一作,二证,三计算”.
2.D 如图,PO是正四棱锥P-ABCD的高,
设底面边长为a,则底面积S1=a2.
因为正四棱锥的侧棱与底面所成的角为45°,
所以∠PAO=45°,
又AO=a,所以PA=×a=a,
所以△PAB是正三角形,所以侧面PAB的面积S2=a2,所以==.
3.C 过点E作EF⊥BD,垂足为F,连接AF,则∠EAF即为直线AE与平面ABD所成的角,不妨设正方形的边长为2,则BF=EF=,AB=2,在△ABF中,由余弦定理可得AF2=AB2+BF2-2AB·BF·cos∠ABF=,所以AF=,在Rt△AEF中,AE2=AF2+EF2=3,所以AE=,故cos∠EAF==.
4.B 由题可知cos 45°=cos θ·cos 30°,∴cos θ=.
5.A 由公式cos θ=cos θ1cos θ2可知A正确.
6.B 因为平面α的一个法向量为n=(2,1,1),直线l的一个方向向量为a=(1,2,3),
所以直线l与平面α所成角的正弦值为|cos
7.B 如图所示,取AC的中点D,以D为原点,BD,DC,DM所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
不妨设AC=2,则A(0,-1,0),M(0,0,2),B(-,0,0),C(0,1,0),B1(-,0,2),
所以=(0,1,2),=(,1,0),=(0,0,2).
设平面BCC1B1的一个法向量为n=(x,y,z),则令x=,则y=-3,z=0,所以n=(,-3,0).
设直线AM与平面BCC1B1所成的角为α,
则sin α=|cos <,n>|==,
即直线AM与平面BCC1B1所成角的正弦值为.
8.B 以D为原点,,,的方向分别为x轴、y轴、z轴的正方向建立如图所示的空间直角坐标系,
则D(0,0,0),A(1,0,0),B(1,1,0),E,A1(1,0,1),∴=(1,1,0),=.设平面BDE的一个法向量为n=(x,y,z),则即令x=1,则y=-1,z=2,∴平面BDE的一个法向量为n=(1,-1,2).∵=(0,-1,1),∴cos<,n>==,又∵<,n>∈[0,π],∴<,n>=,∴直线A1B与平面BDE的夹角为.故选B.
9.答案
解析 由于平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,故AF,AB,AD两两互相垂直,以A为原点,,,的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系,如图所示,
则A(0,0,0),G(a,a,0),B(0,2a,0),C(0,2a,2a),所以=(-a,a,0),=(0,2a,2a),=(a,a,0),
设平面AGC的一个法向量为n=(x,y,z),
则
令x=1,得n=(1,-1,1),
因此直线GB与平面AGC所成角的正弦值为|cos
能力提升练
1.B 在正四面体A-BCD中,E为棱AD的中点,设棱长为a,如图所示,过点A作AO⊥平面BCD,垂足为O,则点O为△BCD的中心,连接DO并延长,交BC于点G,过点E作EF⊥GD于点F,连接FC,则∠ECF即为直线CE与平面BCD所成的角.由GD2=CD2-CG2,得GD=a,所以OD=GD=a.由AO2=AD2-OD2,得AO=a,所以EF=AO=a.又CE=GD=a,所以在Rt△EFC中,sin∠ECF==.故选B.
2.B 连接PB.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则A(3,0,0),B(3,3,0),D1(0,0,4).设P(x,3,z),0
所以HN∥BC,且HN=BC,
又因为B1M∥BC,且B1M=BC,
所以HN∥B1M,且HN=B1M,
所以四边形HNMB1是平行四边形,
所以MN∥B1H,
又因为MN 平面ABB1A1,B1H 平面ABB1A1,
所以MN∥平面ABB1A1.
(2)连接A1M,BM,因为A1B1=A1C1,M是B1C1的中点,所以A1M⊥B1C1.
又因为面A1B1C1⊥面BCC1B1,A1M 面A1B1C1,面A1B1C1∩面BCC1B1=B1C1,
所以A1M⊥面BCC1B1,
所以直线BM为A1B在面BCC1B1内的射影,
所以∠A1BM为直线A1B与平面BCC1B1所成的角.
设AB=2,则A1M=,A1B=2,
所以sin∠A1BM===,
所以∠A1BM=30°,
所以直线A1B与平面BCC1B1所成角的大小为30°.
4.D 如图所示,将正四面体A-BCD放入一个正方体中,且建立空间直角坐标系,设正方体的棱长为3,则A(0,0,3),B(0,3,0),C(3,0,0),D(3,3,3),E(3,1,1),
所以=(3,-3,0),=(3,0,3),=(0,-1,-1),=(-3,0,3).
设=λ=(-3λ,0,3λ),0≤λ≤1,则=+=(-3λ,-1,3λ-1).
设平面BCD的一个法向量为n=(x,y,z),
则即令x=1,则y=1,z=-1,即n=(1,1,-1),
设EF与平面BCD所成的角为α,则sin α=|cos
当λ=0时,sin α=0,
当0<λ≤1时,sin α=,则当=,即λ=时,sin α取得最大值,此时α最大,则sin θ=(sin α)max=.
5.ABC 如图,建立空间直角坐标系,则A1(a,0,a),B1(a,a,a),E,B(a,a,0),D(0,0,0),D1(0,0,a),则=,=(a,a,0),=(a,0,a),=(-a,-a,a),设平面A1BD的一个法向量为n=(x,y,z),则取x=1,则y=z=-1,所以n=(1,-1,-1),所以n·=1×(-a)+(-1)×(-a)+(-1)×=≠0,故B1E不平行于平面A1BD,故A错误;
因为·=(-a)×(-a)+(-a)×(-a)+a×=a2≠0,所以与不垂直,故B错误;
==·B1C1=a3,故C错误;
易知平面CDD1C1的一个法向量为m=(1,0,0),设直线B1E与平面CDD1C1所成的角为θ,则sin θ===,所以cos θ==,
所以tan θ===,故D正确.
6.A 设正方体的棱长为1,=λ(0≤λ≤1).
以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则D(0,0,0),B1(1,1,1),O,P(1-λ,λ,1),所以=.
连接B1D,在正方体ABCD-A1B1C1D1中,易证得B1D⊥平面A1BC1,所以=(-1,-1,-1)是平面A1BC1的一个法向量,
所以sin θ=|cos<,>|
==,
当λ=时,sin θ取得最大值,
当λ=0或λ=1时,sin θ取得最小值.故sin θ∈.
故选A.
7.解析 (1)由已知可得OP=BQ=2,
因为OA=,所以AB=2,
所以正四棱锥P-ABCD的体积V=×S正方形ABCD×PO=×22×2=.
(2)以O为原点,OC,OD,OP所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,易得P(0,0,2),A(-,0,0),B(0,-,0),C(,0,0),Q(0,-,2),所以=(0,,0),=(-,0,2),=(,0,2).
设平面PQC的一个法向量为n=(x0,y0,z0),则即
令x0=,得n=(,0,1).
依题意可得==,
设E(x,y,z),则=(x+,y,z),
所以(x+,y,z)=,解得
故E,所以=.
设直线BE与平面PQC所成的角为θ,
则sin θ=|cos<,n>|===.
因为θ∈,所以θ=arcsin.
故直线BE与平面PQC所成角的大小为arcsin.
8.解析 (1)证明:如图,连接AC,交BD于点O,连接EO,
易证得△ADC≌△ABC,△ADO≌△ABO,
所以∠AOD=∠AOB=90°,
所以AC垂直平分BD.
又EC⊥BD,EC∩AC=C,所以BD⊥平面AEC,
又EO 平面AEC,所以EO⊥BD,
又底面ABCD是圆内接四边形,
所以∠ADC=∠ABC=90°.
在Rt△ADC中,由AD=,CD=1,可得AC=2,AO=,则AC2=AE2+CE2,所以∠AEC=90°,==,
又因为∠EAO=∠CAE,所以△AEO∽△ACE,
所以∠AOE=∠AEC=90°,即EO⊥AC,
又AC,BD 平面ABCD,AC∩BD=O,
所以EO⊥平面ABCD,
又EO 平面BED,所以平面BED⊥平面ABCD.
(2)如图,取AE的中点M,AB的中点N,连接MN,MD,DN,则MN∥BE,
由(1)易知,∠DAC=∠BAC=30°,即∠DAB=60°,
所以△ABD为正三角形,所以DN⊥AB,
又BC⊥AB,所以DN∥BC,又MN∩DN=N,BE∩BC=B,所以平面DMN∥平面EBC,
所以点P在线段MN上.
以O为坐标原点,建立如图所示的空间直角坐标系,
则A,B,E,
M,D,N,
所以=,=,=,=.
设平面ABE的一个法向量为n=(x,y,z),
则即
令x=1,则n=(1,,).
设=λ(0≤λ≤1),可得
=+=.
设直线DP与平面ABE所成的角为θ,
则sin θ==,
因为0≤λ≤1,所以当λ=0时,sin θ取得最大值.
故直线DP与平面ABE所成角的正弦值的最大值为.
9.解析 (1)E是BC的中点,理由如下:
∵平面AME∥平面PCD,平面ABCD∩平面AME=AE,平面ABCD∩平面PCD=CD,∴AE∥CD,
又∵AD∥EC,∴四边形ADCE是平行四边形,
∴EC=AD=1,
又∵BC=2,∴BE=EC,即E是BC的中点.
(2)由题意知PA,AB,AD两两互相垂直.以A为原点,AD,AB,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则A(0,0,0),B(0,2,0),C(2,2,0),D(1,0,0),P(0,0,2),M(0,1,1),
∴=(0,-1,-1),=(1,0,0),=(1,2,0).
设直线MN与平面PAB所成的角为θ,=λ(0≤λ≤1),则=++=(λ+1,2λ-1,-1).
易知n=(1,0,0)为平面PAB的一个法向量,
则sin θ=|cos<,n>|=
=.
令λ+1=t,则t∈[1,2],
则==,
∴当t=,即λ=时,sin θ取得最大值,为,
∴当N是线段DC上靠近C的三等分点时,直线MN与平面PAB所成的角最大,最大角的正弦值为.
