人教B版(2019)选择性必修第一册 第一章 空间向量与立体几何 复习提升 (Word含答案)
文档属性
| 名称 | 人教B版(2019)选择性必修第一册 第一章 空间向量与立体几何 复习提升 (Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 178.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 11:21:03 | ||
图片预览




文档简介
第一章 空间向量与立体几何
本章复习提升
易混易错练
易错点1 混淆向量的共线、共面与线段的共线、共面致错
1.(2020海南中学期中)若=λ+μ(λ,μ∈R),则直线AB与平面CDE的位置关系为 .
2.(2020四川自贡期末)如图,在正方体ABCD-A1B1C1D1中,M,N分别是AB,A1D1的中点,判断直线MN与平面BB1D1D的位置关系,并说明理由.
易错点2 忽略定义、定理中的特殊条件致错
3.(2020湖南长郡中学检测)下列命题中正确的是( )
A.若a与b共线,b与c共线,则a与c共线
B.向量a,b,c共面,即它们所在的直线共面
C.若a∥b,则存在唯一的实数λ,使a=λb
D.零向量是模为0,方向任意的向量
易错点3 忽略向量共线的情况致错
4.(2020河南许昌期末)若向量a=(2,-1,2),b=(-4,2,m),且a 与b 的夹角为钝角,则实数m的取值范围为 .
5.(2020上海复旦附中期末)已知点A(1,2,1),B(3,3,2),C(λ+1,4,3),若,的夹角为锐角,则λ的取值范围为 .
易错点4 对空间向量的夹角的概念理解不清致错
6.(2021江苏常州中学期中)如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,则此时B,D两点间的距离为 .
易错点5 混淆空间角与向量所成角致错
7.(2020山东泰安期末)如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点.
(1)求异面直线PA与DE所成角的余弦值;
(2)求直线AP与平面ABCD所成角的正弦值.
8.(2020河南郑州外国语学校期末)在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(1)求证:BD⊥平面AED;
(2)求二面角F-BD-C的余弦值.
思想方法练
一、函数与方程思想在空间向量与立体几何中的应用
1.(2021北京师范大学昌平附属学校期末)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD的中点.
(1)求证:PA⊥平面ABCD;
(2)求直线PC与平面ACE所成角的正弦值;
(3)在线段BC上是否存在点F,使得点E到平面PAF的距离为 若存在,确定点F的位置;若不存在,请说明理由.
2.(2021江苏连云港月考)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,AD=CD,∠ABC=120°.
(1)求证:平面PAC⊥平面PBD;
(2)若M为PB的中点,N为线段PC上一动点,求直线MN与平面PAC所成角的正弦值的取值范围.
二、转化与化归思想在空间向量与立体几何中的应用
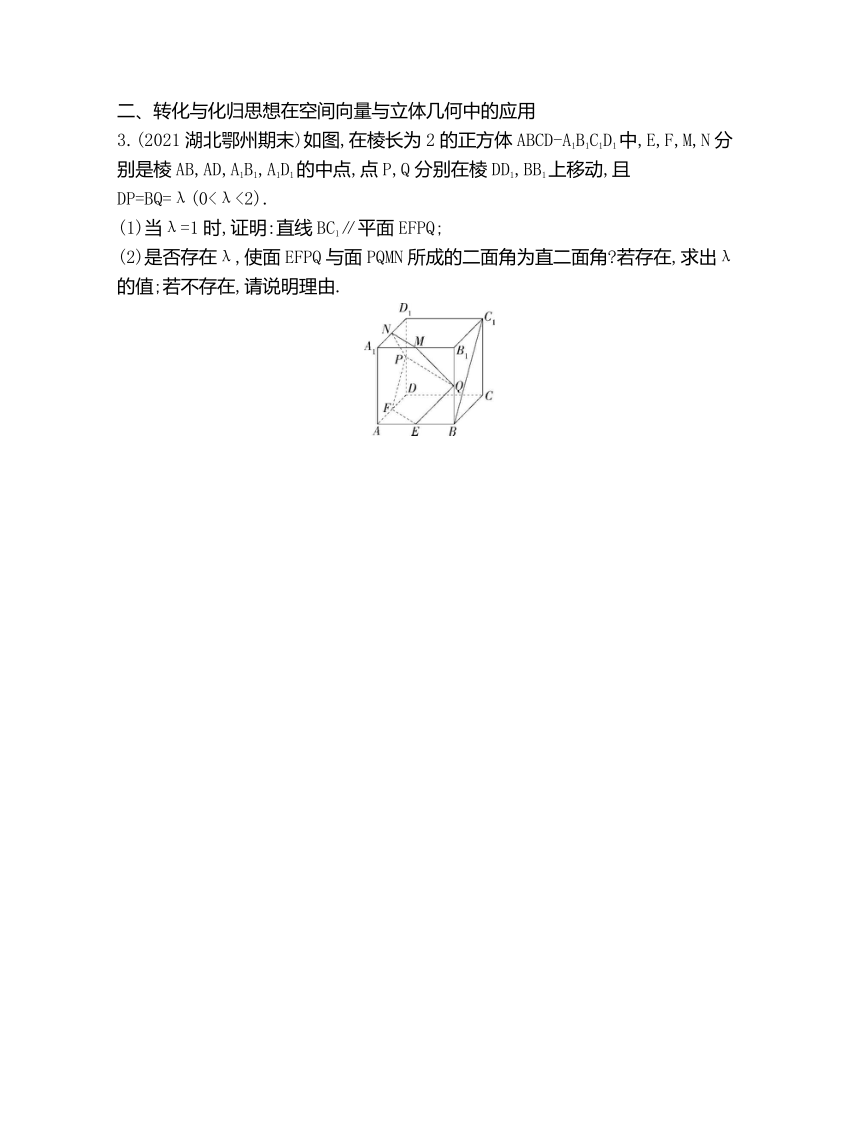
3.(2021湖北鄂州期末)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,证明:直线BC1∥平面EFPQ;
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角 若存在,求出λ的值;若不存在,请说明理由.
答案与分层梯度式解析
第一章 空间向量与立体几何
本章复习提升
易混易错练
1.答案 AB 平面CDE或AB∥平面CDE
解析 由=λ+μ(λ,μ∈R)及共面向量定理可知向量与向量,共面,则直线AB可能在平面CDE内,也可能与平面CDE平行.
易错警示 本题容易因混淆了向量共面和直线共面而错答为AB 平面CDE,向量与向量,共面,直线AB可能在平面CDE内,也可能与平面CDE平行.
2.解析 MN∥平面BB1D1D.理由如下:设正方体的棱长为1,如图,建立空间直角坐标系,
则B(1,1,0),D1(0,0,1),D(0,0,0),M,N,
∴=,=(1,1,0),=(0,0,1).
设平面BB1D1D的一个法向量为n=(x,y,z),
则即
令x=1,则y=-1,z=0,
∴n=(1,-1,0)是平面BB1D1D的一个法向量.
∵·n=0,MN 平面BB1D1D,
∴MN∥平面BB1D1D.
易错警示 本题容易因忽视MN 平面BB1D1D,而直接由·n=0,得MN∥平面BB1D1D,造成步骤不完整,实际上,当·n=0时,MN∥平面BB1D1D或MN 平面BB1D1D.
3.D 由于零向量与任意向量共线,所以当b为零向量时,a与c的关系不确定,故A错;当向量a,b,c共面时,它们所在的直线不一定共面,故B错;在共线向量定理中,当b不是零向量时,才存在唯一的实数λ,使a=λb,否则λ可能不存在,故C错;D显然正确.
易错警示 本题容易忽略零向量的特殊性和共线向量定理中的限制条件而误认为A,C正确.
4.答案 (-∞,-4)∪(-4,5)
解析 ∵a 与b 的夹角为钝角,
∴a·b=-8-2+2m<0,解得m<5,
又由a∥b,得m=-4,
∴实数m的取值范围为(-∞,-4)∪(-4,5).
易错警示 本题容易忽略两向量方向相反的情形,只由a·b=-8-2+2m<0,解得m<5.
5.答案 (-2,4)∪(4,+∞)
解析 易知=(2,1,1),=(λ,2,2).
∵,的夹角为锐角,∴·=2λ+2+2>0,解得λ>-2,
又由∥ 得λ=4,
∴λ的取值范围为(-2,4)∪(4,+∞).
6.答案 或2
解析 由题意得∠ACD=∠BAC=90°,所以·=0,·=0.
因为折起后AB与CD成60°角,所以<,>=60°或<,>=120°.
又=++,
所以||2=||2+||2+||2+2·+2·+2·=3+2×1×1×cos<,>,
所以当<,>=60°时,||2=4,此时B,D两点间的距离为2;
当<,>=120°时,||2=2,此时B,D两点间的距离为.
7.解析 取DC的中点O,连接PO,
∵△PDC为正三角形,∴PO⊥DC.
又∵平面PDC⊥平面ABCD,平面PDC∩平面ABCD=DC,∴PO⊥平面ABCD.
建立如图所示的空间直角坐标系Oxyz,
则P,A,C,D.
(1)设异面直线PA与DE所成的角为θ.
∵E为PC的中点,∴E,
∴=,=,∴·=a×+a×=-a2,||=a,||=a,∴cos<,>===-.∵cos θ=|cos<,>|,
∴异面直线PA与DE所成角的余弦值为.
(2)设直线AP与平面ABCD所成的角为α,
易知平面ABCD的一个法向量n=0,0,a,
∴cos<,n>===-.
∵sin α=|cos<,n>|=,
∴直线AP与平面ABCD所成角的正弦值为.
易错警示 当两条异面直线的方向向量的夹角为锐角或直角时,这个角就是这两条异面直线所成的角;当两条异面直线的方向向量的夹角为钝角时,其补角是这两条异面直线所成的角.求解直线和平面所成的角θ时,要注意直线的方向向量n与平面的法向量a的夹角和所求角θ之间的关系,线面角的正弦值等于两向量夹角的余弦值的绝对值.它们的关系是sin θ=|cos|.
8.解析 (1)证明:因为四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
所以∠ADC=∠BCD=120°.
又CB=CD,所以∠CDB=30°,
所以∠ADB=90°,即AD⊥BD.
又AE⊥BD,且AE∩AD=A,AE,AD 平面AED,
所以BD⊥平面AED.
(2)连接AC.易得AC⊥BC.又FC⊥平面ABCD,所以CA,CB,CF两两垂直.
以C为坐标原点,CA,CB,CF所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
不妨设CB=1,
则C(0,0,0),B(0,1,0),D,F(0,0,1),
所以=,=(0,-1,1).
设平面BDF的一个法向量为m=(x,y,z),
则即
取z=1,则m=(,1,1).
易知=(0,0,1)是平面BDC的一个法向量,
则cos===,
易知二面角F-BD-C为锐二面角,
所以二面角F-BD-C的余弦值为.
易错警示 应用向量法求出的两个法向量的夹角的大小与二面角的大小可能相等也可能互补,一般结合实际图形判断所求二面角是钝二面角还是锐二面角.
思想方法练
1.解析 (1)证明:∵四边形ABCD为正方形,∴BC⊥AB,CD⊥AD,
∵PB⊥BC,BC⊥AB,PB∩AB=B,PB,AB 平面PAB,∴BC⊥平面PAB.
∵PA 平面PAB,∴PA⊥BC,
同理PA⊥CD,∵BC∩CD=C,BC,CD 平面ABCD,∴PA⊥平面ABCD.
(2)以A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则A(0,0,0),C(2,2,0),P(0,0,2),E(0,1,1),
∴=(2,2,0),=(0,1,1),=(2,2,-2),
设平面ACE的一个法向量为m=(x,y,z),
则取y=1,则m=(-1,1,-1),
∴cos===,
∴直线PC与平面ACE所成角的正弦值为.
(3)存在.设点F(2,t,0)(0≤t≤2),则=(2,t,0),=(0,0,2),
设平面PAF的一个法向量为n=(a,b,c),
则取a=t,则n=(t,-2,0),
∴点E到平面PAF的距离d===.∵t>0,∴t=1.
因此,当F为线段BC的中点时,点E到平面PAF的距离为.
思想方法 空间向量中应用函数与方程思想主要涉及与空间向量运算以及空间角相关的取值范围问题,一般有两种解决途径:
(1)充分挖掘题设中的不等关系,构建以待求字母为元的不等式(组)求解;(2)充分应用题设中的等量关系构造函数或方程求解.
2.解析 (1)证明:取AC的中点O,连接BO,DO,因为AB=BC,所以BO⊥AC.因为AD=CD,所以DO⊥AC,
所以B,O,D三点共线,所以BD⊥AC.
因为PA⊥平面ABCD,BD 平面ABCD,
所以BD⊥PA.
又因为PA∩AC=A,PA,AC 平面PAC,
所以BD⊥平面PAC.
因为BD 平面PBD,所以平面PAC⊥平面PBD.
(2)以O为坐标原点,OC,OD所在直线分别为x轴、y轴,过点O且平行于PA的直线为z轴建立如图所示的空间直角坐标系,
则C(,0,0),P(-,0,2),B(0,-1,0).
因为M为PB的中点,所以M.
设=λ(0≤λ≤1),
则N(2λ-,0,2-2λ),
所以=.
由(1)知BD⊥平面PAC,所以平面PAC的一个法向量为n=(0,1,0).
设直线MN与平面PAC所成的角为θ,
则sin θ=|cos<,n>|===,0≤λ≤1,
将直线和平面所成的角的正弦值用含参的式子表示,利用二次函数性质求出最值,体现了函数思想.
故当λ=时,sin θ取得最大值,为,当λ=1时,sin θ取得最小值,为.
所以≤sin θ≤,即直线MN与平面PAC所成角的正弦值的取值范围为.
3.解析 (1)证明:以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则B(2,2,0),C1(0,2,2),F(1,0,0),当λ=1时,P(0,0,1).
∴=(-2,0,2),=(-1,0,1),∴=2,∴BC1∥FP.
∵BC1 平面EFPQ,FP 平面EFPQ,∴BC1∥平面EFPQ.
(2)由(1)知E(2,1,0),F(1,0,0),P(0,0,λ),N(1,0,2),M(2,1,2),则=(-1,-1,0),=(-1,0,λ),=(-1,-1,0),=(-1,0,λ-2),
设平面EFPQ的一个法向量为m=(x1,y1,z1),
由可得取x1=λ,则y1=-λ,z1=1,∴m=(λ,-λ,1).
设平面PQMN的一个法向量为n=(x2,y2,z2),
由可得取x2=λ-2,则y2=2-λ,z2=1,∴n=(λ-2,2-λ,1).
若存在λ,使得面EFPQ与面PQMN所成的二面角为直二面角,则m⊥n,
将两个平面垂直转化为两个平面的法向量垂直,将几何问题转化为代数问题求解.
∴m·n=λ(λ-2)-λ(2-λ)+1=0,整理可得2λ2-4λ+1=0,
解得λ=1±,均满足题意.
因此,存在λ=1±,使得面EFPQ与面PQMN所成的二面角为直二面角.
思想方法 转化与化归思想在空间向量中主要有两大应用方向:
(1)将证明空间中的平行或垂直问题转化为两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量共线或垂直问题;
(2)将空间角的问题转化为空间向量夹角的问题,如:线线角问题转化为两直线方向向量的夹角问题,线面角问题转化为直线的方向向量与平面法向量的夹角问题,面面角问题转化为两个平面法向量的夹角问题.
本章复习提升
易混易错练
易错点1 混淆向量的共线、共面与线段的共线、共面致错
1.(2020海南中学期中)若=λ+μ(λ,μ∈R),则直线AB与平面CDE的位置关系为 .
2.(2020四川自贡期末)如图,在正方体ABCD-A1B1C1D1中,M,N分别是AB,A1D1的中点,判断直线MN与平面BB1D1D的位置关系,并说明理由.
易错点2 忽略定义、定理中的特殊条件致错
3.(2020湖南长郡中学检测)下列命题中正确的是( )
A.若a与b共线,b与c共线,则a与c共线
B.向量a,b,c共面,即它们所在的直线共面
C.若a∥b,则存在唯一的实数λ,使a=λb
D.零向量是模为0,方向任意的向量
易错点3 忽略向量共线的情况致错
4.(2020河南许昌期末)若向量a=(2,-1,2),b=(-4,2,m),且a 与b 的夹角为钝角,则实数m的取值范围为 .
5.(2020上海复旦附中期末)已知点A(1,2,1),B(3,3,2),C(λ+1,4,3),若,的夹角为锐角,则λ的取值范围为 .
易错点4 对空间向量的夹角的概念理解不清致错
6.(2021江苏常州中学期中)如图,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,则此时B,D两点间的距离为 .
易错点5 混淆空间角与向量所成角致错
7.(2020山东泰安期末)如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点.
(1)求异面直线PA与DE所成角的余弦值;
(2)求直线AP与平面ABCD所成角的正弦值.
8.(2020河南郑州外国语学校期末)在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(1)求证:BD⊥平面AED;
(2)求二面角F-BD-C的余弦值.
思想方法练
一、函数与方程思想在空间向量与立体几何中的应用
1.(2021北京师范大学昌平附属学校期末)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD的中点.
(1)求证:PA⊥平面ABCD;
(2)求直线PC与平面ACE所成角的正弦值;
(3)在线段BC上是否存在点F,使得点E到平面PAF的距离为 若存在,确定点F的位置;若不存在,请说明理由.
2.(2021江苏连云港月考)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,AD=CD,∠ABC=120°.
(1)求证:平面PAC⊥平面PBD;
(2)若M为PB的中点,N为线段PC上一动点,求直线MN与平面PAC所成角的正弦值的取值范围.
二、转化与化归思想在空间向量与立体几何中的应用
3.(2021湖北鄂州期末)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,证明:直线BC1∥平面EFPQ;
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角 若存在,求出λ的值;若不存在,请说明理由.
答案与分层梯度式解析
第一章 空间向量与立体几何
本章复习提升
易混易错练
1.答案 AB 平面CDE或AB∥平面CDE
解析 由=λ+μ(λ,μ∈R)及共面向量定理可知向量与向量,共面,则直线AB可能在平面CDE内,也可能与平面CDE平行.
易错警示 本题容易因混淆了向量共面和直线共面而错答为AB 平面CDE,向量与向量,共面,直线AB可能在平面CDE内,也可能与平面CDE平行.
2.解析 MN∥平面BB1D1D.理由如下:设正方体的棱长为1,如图,建立空间直角坐标系,
则B(1,1,0),D1(0,0,1),D(0,0,0),M,N,
∴=,=(1,1,0),=(0,0,1).
设平面BB1D1D的一个法向量为n=(x,y,z),
则即
令x=1,则y=-1,z=0,
∴n=(1,-1,0)是平面BB1D1D的一个法向量.
∵·n=0,MN 平面BB1D1D,
∴MN∥平面BB1D1D.
易错警示 本题容易因忽视MN 平面BB1D1D,而直接由·n=0,得MN∥平面BB1D1D,造成步骤不完整,实际上,当·n=0时,MN∥平面BB1D1D或MN 平面BB1D1D.
3.D 由于零向量与任意向量共线,所以当b为零向量时,a与c的关系不确定,故A错;当向量a,b,c共面时,它们所在的直线不一定共面,故B错;在共线向量定理中,当b不是零向量时,才存在唯一的实数λ,使a=λb,否则λ可能不存在,故C错;D显然正确.
易错警示 本题容易忽略零向量的特殊性和共线向量定理中的限制条件而误认为A,C正确.
4.答案 (-∞,-4)∪(-4,5)
解析 ∵a 与b 的夹角为钝角,
∴a·b=-8-2+2m<0,解得m<5,
又由a∥b,得m=-4,
∴实数m的取值范围为(-∞,-4)∪(-4,5).
易错警示 本题容易忽略两向量方向相反的情形,只由a·b=-8-2+2m<0,解得m<5.
5.答案 (-2,4)∪(4,+∞)
解析 易知=(2,1,1),=(λ,2,2).
∵,的夹角为锐角,∴·=2λ+2+2>0,解得λ>-2,
又由∥ 得λ=4,
∴λ的取值范围为(-2,4)∪(4,+∞).
6.答案 或2
解析 由题意得∠ACD=∠BAC=90°,所以·=0,·=0.
因为折起后AB与CD成60°角,所以<,>=60°或<,>=120°.
又=++,
所以||2=||2+||2+||2+2·+2·+2·=3+2×1×1×cos<,>,
所以当<,>=60°时,||2=4,此时B,D两点间的距离为2;
当<,>=120°时,||2=2,此时B,D两点间的距离为.
7.解析 取DC的中点O,连接PO,
∵△PDC为正三角形,∴PO⊥DC.
又∵平面PDC⊥平面ABCD,平面PDC∩平面ABCD=DC,∴PO⊥平面ABCD.
建立如图所示的空间直角坐标系Oxyz,
则P,A,C,D.
(1)设异面直线PA与DE所成的角为θ.
∵E为PC的中点,∴E,
∴=,=,∴·=a×+a×=-a2,||=a,||=a,∴cos<,>===-.∵cos θ=|cos<,>|,
∴异面直线PA与DE所成角的余弦值为.
(2)设直线AP与平面ABCD所成的角为α,
易知平面ABCD的一个法向量n=0,0,a,
∴cos<,n>===-.
∵sin α=|cos<,n>|=,
∴直线AP与平面ABCD所成角的正弦值为.
易错警示 当两条异面直线的方向向量的夹角为锐角或直角时,这个角就是这两条异面直线所成的角;当两条异面直线的方向向量的夹角为钝角时,其补角是这两条异面直线所成的角.求解直线和平面所成的角θ时,要注意直线的方向向量n与平面的法向量a的夹角和所求角θ之间的关系,线面角的正弦值等于两向量夹角的余弦值的绝对值.它们的关系是sin θ=|cos
8.解析 (1)证明:因为四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
所以∠ADC=∠BCD=120°.
又CB=CD,所以∠CDB=30°,
所以∠ADB=90°,即AD⊥BD.
又AE⊥BD,且AE∩AD=A,AE,AD 平面AED,
所以BD⊥平面AED.
(2)连接AC.易得AC⊥BC.又FC⊥平面ABCD,所以CA,CB,CF两两垂直.
以C为坐标原点,CA,CB,CF所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
不妨设CB=1,
则C(0,0,0),B(0,1,0),D,F(0,0,1),
所以=,=(0,-1,1).
设平面BDF的一个法向量为m=(x,y,z),
则即
取z=1,则m=(,1,1).
易知=(0,0,1)是平面BDC的一个法向量,
则cos
易知二面角F-BD-C为锐二面角,
所以二面角F-BD-C的余弦值为.
易错警示 应用向量法求出的两个法向量的夹角的大小与二面角的大小可能相等也可能互补,一般结合实际图形判断所求二面角是钝二面角还是锐二面角.
思想方法练
1.解析 (1)证明:∵四边形ABCD为正方形,∴BC⊥AB,CD⊥AD,
∵PB⊥BC,BC⊥AB,PB∩AB=B,PB,AB 平面PAB,∴BC⊥平面PAB.
∵PA 平面PAB,∴PA⊥BC,
同理PA⊥CD,∵BC∩CD=C,BC,CD 平面ABCD,∴PA⊥平面ABCD.
(2)以A为坐标原点,AB,AD,AP所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,
则A(0,0,0),C(2,2,0),P(0,0,2),E(0,1,1),
∴=(2,2,0),=(0,1,1),=(2,2,-2),
设平面ACE的一个法向量为m=(x,y,z),
则取y=1,则m=(-1,1,-1),
∴cos
∴直线PC与平面ACE所成角的正弦值为.
(3)存在.设点F(2,t,0)(0≤t≤2),则=(2,t,0),=(0,0,2),
设平面PAF的一个法向量为n=(a,b,c),
则取a=t,则n=(t,-2,0),
∴点E到平面PAF的距离d===.∵t>0,∴t=1.
因此,当F为线段BC的中点时,点E到平面PAF的距离为.
思想方法 空间向量中应用函数与方程思想主要涉及与空间向量运算以及空间角相关的取值范围问题,一般有两种解决途径:
(1)充分挖掘题设中的不等关系,构建以待求字母为元的不等式(组)求解;(2)充分应用题设中的等量关系构造函数或方程求解.
2.解析 (1)证明:取AC的中点O,连接BO,DO,因为AB=BC,所以BO⊥AC.因为AD=CD,所以DO⊥AC,
所以B,O,D三点共线,所以BD⊥AC.
因为PA⊥平面ABCD,BD 平面ABCD,
所以BD⊥PA.
又因为PA∩AC=A,PA,AC 平面PAC,
所以BD⊥平面PAC.
因为BD 平面PBD,所以平面PAC⊥平面PBD.
(2)以O为坐标原点,OC,OD所在直线分别为x轴、y轴,过点O且平行于PA的直线为z轴建立如图所示的空间直角坐标系,
则C(,0,0),P(-,0,2),B(0,-1,0).
因为M为PB的中点,所以M.
设=λ(0≤λ≤1),
则N(2λ-,0,2-2λ),
所以=.
由(1)知BD⊥平面PAC,所以平面PAC的一个法向量为n=(0,1,0).
设直线MN与平面PAC所成的角为θ,
则sin θ=|cos<,n>|===,0≤λ≤1,
将直线和平面所成的角的正弦值用含参的式子表示,利用二次函数性质求出最值,体现了函数思想.
故当λ=时,sin θ取得最大值,为,当λ=1时,sin θ取得最小值,为.
所以≤sin θ≤,即直线MN与平面PAC所成角的正弦值的取值范围为.
3.解析 (1)证明:以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则B(2,2,0),C1(0,2,2),F(1,0,0),当λ=1时,P(0,0,1).
∴=(-2,0,2),=(-1,0,1),∴=2,∴BC1∥FP.
∵BC1 平面EFPQ,FP 平面EFPQ,∴BC1∥平面EFPQ.
(2)由(1)知E(2,1,0),F(1,0,0),P(0,0,λ),N(1,0,2),M(2,1,2),则=(-1,-1,0),=(-1,0,λ),=(-1,-1,0),=(-1,0,λ-2),
设平面EFPQ的一个法向量为m=(x1,y1,z1),
由可得取x1=λ,则y1=-λ,z1=1,∴m=(λ,-λ,1).
设平面PQMN的一个法向量为n=(x2,y2,z2),
由可得取x2=λ-2,则y2=2-λ,z2=1,∴n=(λ-2,2-λ,1).
若存在λ,使得面EFPQ与面PQMN所成的二面角为直二面角,则m⊥n,
将两个平面垂直转化为两个平面的法向量垂直,将几何问题转化为代数问题求解.
∴m·n=λ(λ-2)-λ(2-λ)+1=0,整理可得2λ2-4λ+1=0,
解得λ=1±,均满足题意.
因此,存在λ=1±,使得面EFPQ与面PQMN所成的二面角为直二面角.
思想方法 转化与化归思想在空间向量中主要有两大应用方向:
(1)将证明空间中的平行或垂直问题转化为两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量共线或垂直问题;
(2)将空间角的问题转化为空间向量夹角的问题,如:线线角问题转化为两直线方向向量的夹角问题,线面角问题转化为直线的方向向量与平面法向量的夹角问题,面面角问题转化为两个平面法向量的夹角问题.
