人教B版(2019)选择性必修第一册 第一章 空间向量与立体几何 综合拔高练 (Word含答案)
文档属性
| 名称 | 人教B版(2019)选择性必修第一册 第一章 空间向量与立体几何 综合拔高练 (Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 353.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 11:21:57 | ||
图片预览



文档简介
第一章 空间向量与立体几何
综合拔高练
五年高考练
考点1 用空间向量判断线面位置关系
1.(2021新高考Ⅰ,12)在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则( )
A.当λ=1时,△AB1P的周长为定值
B.当μ=1时,三棱锥P-A1BC的体积为定值
C.当λ=时,有且仅有一个点P,使得A1P⊥BP
D.当μ=时,有且仅有一个点P,使得A1B⊥平面AB1P
2.(2019江苏,16)如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:
(1)A1B1∥平面DEC1;
(2)BE⊥C1E.
考点2 用空间向量求空间中的角
3.(2017课标全国Ⅲ理,16)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是 .(填写所有正确结论的编号)
4.(2021浙江,19)如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC=4,PA=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.
(1)证明:AB⊥PM;
(2)求直线AN与平面PDM所成角的正弦值.
5.(2020新高考Ⅰ,20)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
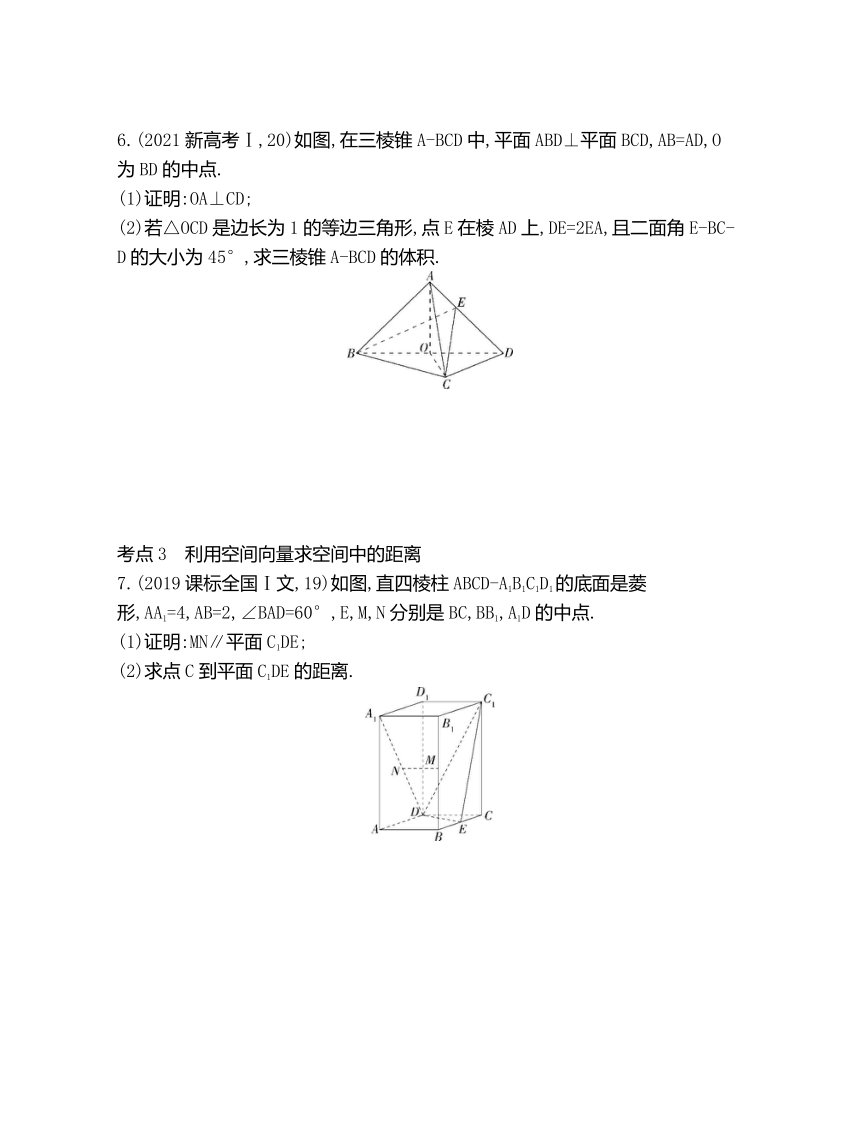
6.(2021新高考Ⅰ,20)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.
(1)证明:OA⊥CD;
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.
考点3 利用空间向量求空间中的距离
7.(2019课标全国Ⅰ文,19)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
考点4 用空间向量解决探究性问题
8.(2021全国甲,19)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
(1)证明:BF⊥DE;
(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小
三年模拟练
应用实践
1.(2022河北石家庄第十七中学月考)现有以下命题:①若a∥b,则存在唯一的实数λ,使得a=λb;②若a·b=b·c,则a=c或b=0;③若{a,b,c}为空间向量的一组基底,则{a+b,b+c,c+a}构成空间向量的另一组基底;④(a·b)·(c·d)=(d·c)·(b·a)一定成立.其中真命题的个数为( )
A.4 B.3 C.2 D.1
2.(2022广东广州第七中学检测)已知三棱锥S-ABC中,SA=SB=SC=1,且SA,SB,SC两两垂直,P是三棱锥S-ABC外接球面上一动点,则点P到平面ABC的距离的最大值是( )
A. B. C. D.
3.(2021江苏常州中学高二期中)如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为直角三角形,且∠BAC=∠BCD=90°,AB=AC,CD=BC=1,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AD成30°角,则线段PA的长的取值范围是( )
A. B.
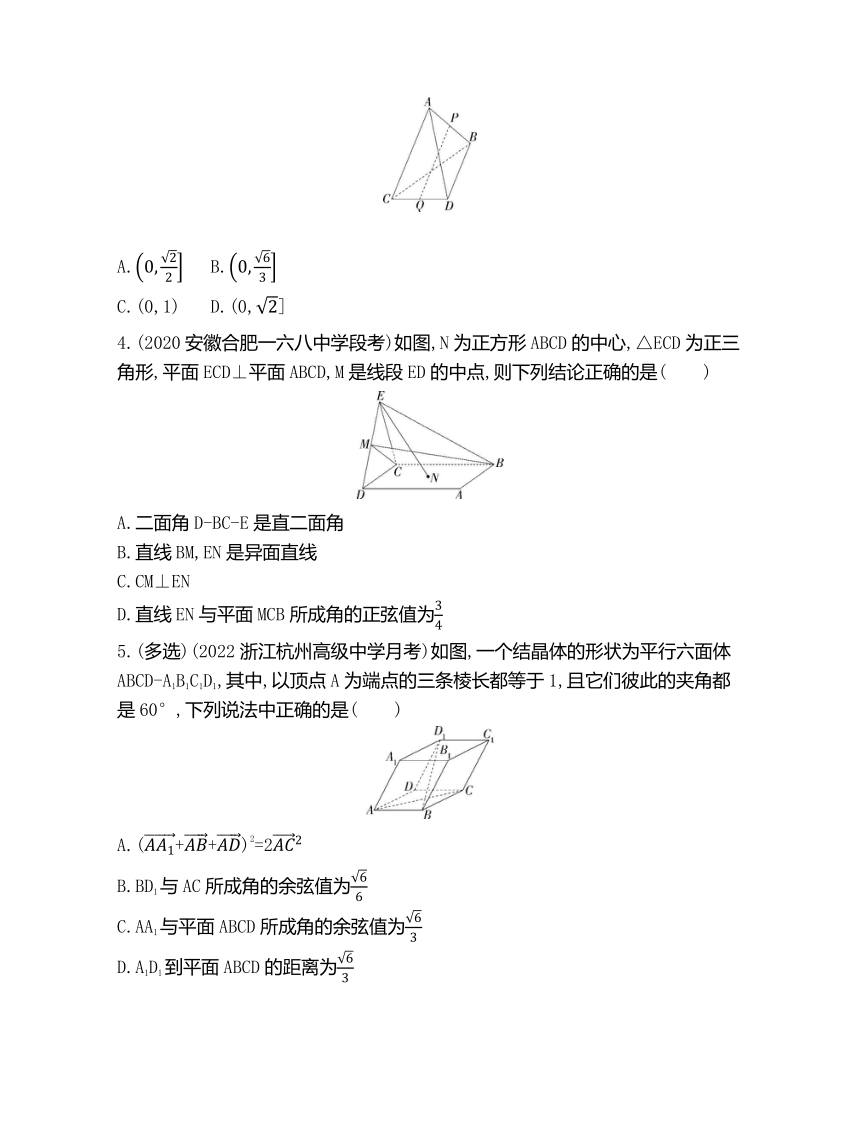
C.(0,1) D.(0,]
4.(2020安徽合肥一六八中学段考)如图,N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则下列结论正确的是( )
A.二面角D-BC-E是直二面角
B.直线BM,EN是异面直线
C.CM⊥EN
D.直线EN与平面MCB所成角的正弦值为
5.(多选)(2022浙江杭州高级中学月考)如图,一个结晶体的形状为平行六面体ABCD-A1B1C1D1,其中,以顶点A为端点的三条棱长都等于1,且它们彼此的夹角都是60°,下列说法中正确的是( )
A.(++)2=2
B.BD1与AC所成角的余弦值为
C.AA1与平面ABCD所成角的余弦值为
D.A1D1到平面ABCD的距离为
6.(2022北京大兴第一中学检测)在空间中,四个不共线的向量,,,两两间的夹角均为α,则cos α的大小为 .
7.(2022山东平邑第一中学期中)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,∠ABC=∠BAD=,PA=AD=2,AB=BC=1.
(1)求平面PAB与平面PCD所成锐二面角的余弦值;
(2)定义两条异面直线之间的距离为其中一条直线上任意一点到另一条直线距离的最小值,利用此定义求异面直线PB与CD之间的距离.
8.如图1,在矩形ABCD中,AB=BC,将矩形ABCD折起,使点A与点C重合,折痕为EF,展开后连接AF,CE,以AF和EF为折痕,将四边形ABFE折起,使点B落在线段FC上,将△CDE向上折起,使平面DEC⊥平面EFC,如图2.
(1)证明:平面ABE⊥平面EFC;
(2)求锐二面角A-BE-D的正弦值.
9.(2021江苏镇江第一中学期末)如图,四棱锥S-ABCD的底面ABCD是直角梯形,∠ABC=90°,AD∥BC,侧面△SCD为钝角三角形,CD=SD,平面SCD⊥平面ABCD,M是棱SA上的动点,AB=AD=BC.
(1)求证:平面MBD⊥平面SCD;
(2)若直线SD与底面ABCD所成的角为60°,是否存在点M使得二面角A-BD-M的余弦值为 若存在,确定点M的位置;若不存在,请说明理由.
答案与分层梯度式解析
第一章 空间向量与立体几何
综合拔高练
五年高考练
1.BD 选项A,当λ=1时,点P在线段CC1上,设CP=x(0≤x≤1),若x=0,则△AB1P即为△AB1C,此时△AB1P的周长为2+1;若x=1,则△AB1P即为△AB1C1,此时△AB1P的周长为2+1.若0在Rt△PCA中,PA=,
在Rt△B1C1P中,PB1==,
而AB1=,所以△AB1P的周长为++,不为定值,故选项A错误;
选项B,当μ=1时,点P在线段B1C1上,
因为B1C1∥BC,B1C1 平面A1BC,BC 平面A1BC,
所以B1C1∥平面A1BC,
所以直线B1C1上的任何一点到平面A1BC的距离均相等,
所以三棱锥P-A1BC的体积为定值,故选项B正确;
取BC,B1C1的中点分别为O,O1,连接OO1,AO,易知OO1⊥平面ABC,AO⊥BC,以OB,OA,OO1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则B,A,A1,选项C,当λ=时,点P在线段OO1上,设P(0,0,z)(0≤z≤1),则=,=,若A1P⊥BP,则·=0,
即z(z-1)=0,解得z=0或z=1,即当λ=时,存在两个点P,使得A1P⊥BP,故选项C错误;
选项D,当μ=时,点P在线段MN上(M,N分别是线段BB1,CC1的中点),
设P,则=,
若A1B⊥平面AB1P,则A1B⊥AP,则·=0,
即·=x+-=0,解得x=-,所以P,易验证此时满足A1B⊥平面AB1P,
所以当μ=时,有且仅有一个点P,使得A1B⊥平面AB1P,故选项D正确.故选BD.
2.证明 (1)取A1C1的中点E1,连接EE1.
由题易得,EC,EB,EE1两两垂直,以E为原点,EC,EB,EE1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图.
设AC=2c,AB=b,AA1=a(c>0,a>0),
则E(0,0,0),B(0,,0),D,A1(-c,0,a),B1(0,,a),C1(c,0,a),
所以=(c,,0),=,
所以=2,所以∥,
所以A1B1∥ED.
因为ED 平面DEC1,A1B1 平面DEC1,
所以A1B1∥平面DEC1.
(2)由(1)得=(0,,0),=(c,0,a),
而·=0,所以⊥,
所以BE⊥C1E.
3.答案 ②③
解析 过点C作直线a1∥a,b1∥b,则直线AC,a1,b1两两垂直.不妨分别以a1,b1,AC所在直线为x轴、y轴、z轴建立空间直角坐标系,取n1=(1,0,0)为a1的方向向量,n2=(0,1,0)为b1的方向向量,令A(0,0,1).可设B(cos θ,sin θ,0),则=(cos θ,sin θ,-1).
当直线AB与a成60°角时,|cos|=,
∴|cos θ|=,|sin θ|=,
∴|cos|=,
即AB与b所成角也是60°.
∵|cos|==≤,
∴直线AB与a所成角的最小值为45°.
综上,②和③是正确的,①和④是错误的.
4.解析 (1)证明:在△CDM中,DC=1,MC=2,∠DCM=60°,则DM=,所以CD⊥DM.
又因为CD⊥PD,所以CD⊥平面PDM.
因此CD⊥PM.
又因为AB∥CD,所以AB⊥PM.
(2)如图,以D为原点,分别以射线DM,DC为x轴,y轴的正半轴,建立空间直角坐标系Dxyz.
则A(2,-2,0),C(0,1,0),M(,0,0),设P(,0,z0),z0>0,
因为PA=,所以z0=2,
故P(,0,2),N,
所以=,=(,0,2),=(,0,0).
设平面PDM的一个法向量为n=(x,y,z),
由得取n=(0,1,0).
设直线AN与平面PDM所成角为α,
所以sin α=|cos<,n>|==.
因此,直线AN与平面PDM所成角的正弦值为.
5.解析 (1)证明:因为PD⊥底面ABCD,所以PD⊥AD.又底面ABCD为正方形,所以AD⊥DC.因此AD⊥平面PDC.
因为AD∥BC,AD 平面PBC,
所以AD∥平面PBC.
由已知得l∥AD.因此l⊥平面PDC.
(2)以D为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系Dxyz,则D(0,0,0),C(0,1,0),B(1,1,0),P(0,0,1),=(0,1,0),=(1,1,-1).
由(1)可设Q(a,0,1),则=(a,0,1).
设n=(x,y,z)是平面QCD的一个法向量,则
即可取n=(-1,0,a).
所以cos==.
设PB与平面QCD所成的角为θ,
则sin θ=×=.
因为≤,当且仅当a=1时等号成立,所以PB与平面QCD所成角的正弦值的最大值为.
6.解析 (1)证明:在△ABD中,∵AB=AD,O为BD的中点,∴AO⊥BD,又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO 平面ABD,∴AO⊥平面BCD,又CD 平面BCD,∴AO⊥CD.
(2)由OC=OD=OB得BC⊥CD,由(1)知AO⊥平面BCD,以C为原点,,,的方向分别为x轴、y轴、z轴正方向建立空间直角坐标系,如图所示,则C(0,0,0),B(0,,0),设AO=a.
则E,∴=(0,,0),=,设平面EBC的法向量为n=(x,y,z),则即令x=a,则z=-1,∴n=(a,0,-1),
易知平面BCD的一个法向量为m=(0,0,1),
由题可知|cos|===,∴a=1,即AO=1,
∴VA-BCD=S△BCD·AO=××1××1=,
故三棱锥A-BCD的体积为.
7.解析 (1)证明:∵直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点,
∴DD1⊥平面ABCD,DE⊥AD,
以D为原点,DA,DE,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
则M(1,,2),N(1,0,2),D(0,0,0),E(0,,0),C1(-1,,4),∴=(0,-,0),=(-1,,4),=(0,,0),
设平面C1DE的一个法向量为n=(x,y,z),
则即
取z=1,则n=(4,0,1).
∵·n=0,MN 平面C1DE,
∴MN∥平面C1DE.
(2)由(1)得C(-1,,0),∴=(-1,,0),
而平面C1DE的一个法向量为n=(4,0,1),
∴点C到平面C1DE的距离d===.
8.解析 ∵BF⊥A1B1,B1B⊥A1B1,BF∩B1B=B,
∴A1B1⊥平面B1C1CB,∵AB∥A1B1,∴AB⊥平面B1C1CB,
又∵BC 平面B1C1CB,∴AB⊥BC.
以B为坐标原点,BA,BC,BB1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则B(0,0,0),F(0,2,1),E(1,1,0),∴=(0,2,1),设B1D=a(0≤a≤2),则D(a,0,2),则=(1-a,1,-2).
(1)证明:∵·=(0,2,1)·(1-a,1,-2)=0×(1-a)+2×1+1×(-2)=0,∴BF⊥DE.
(2)=(-1,1,1),=(a,-2,1),
设平面DFE的法向量为n=(x,y,z),
则
不妨设x=1,则y=,z=,∴n=.
易知m=(1,0,0)是平面BB1C1C的一个法向量.
设平面BB1C1C与平面DEF所成的锐二面角的大小为θ,
则cos θ=|cos|===≤=,
∴sin θ=≥,故当a=,即B1D=时,平面BB1C1C与平面DFE所成的二面角的正弦值最小,最小值为.
三年模拟练
1.C 当b=0时,①显然不成立,
当a⊥b,且b⊥c时,a·b=b·c=0,不能说明a=c或b=0,故②错误;
若{a,b,c}为空间向量的一组基底,则a,b,c不共面,所以a+b,b+c,c+a也不共面,则{a+b,b+c,c+a}构成空间向量的另一组基底,故③正确;
因为a·b=b·a,c·d=d·c,所以(a·b)·(c·d)=(d·c)·(b·a),故④正确.
2.C ∵SA,SB,SC两两垂直,且SA=SB=SC=1,∴以SA,SB,SC为棱长补作正方体MNQB-ADCS,如图.以B为原点,BM,BQ,BS所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则B(0,0,0),A(1,0,1),C(0,1,1),N(1,1,0),∴=(1,0,1),=(0,1,1),=(1,1,0).
设平面ABC的一个法向量为n=(x,y,z),
则取x=1,则y=1,z=-1,∴n=(1,1,-1),
三棱锥S-ABC的外接球就是棱长为1的正方体MNQB-ADCS的外接球.
∵点P是三棱锥S-ABC外接球面上一动点,
∴由正方体与球的几何性质可得,当点P与点N重合时,点P到平面ABC的距离最大,
∴点P到平面ABC的距离的最大值为==.
3.C 如图,以C为原点,CD所在直线为x轴,CB所在直线为y轴,过C且与平面BCD垂直的直线为z轴,建立空间直角坐标系,则C(0,0,0),A(0,1,1),B(0,2,0),D(1,0,0),设Q(q,0,0)(0≤q<1),设=λ=(0,λ,-λ)(0<λ≤1),则=-(+)=(q,0,0)-(0,1,1)-(0,λ,-λ)=(q,-1-λ,λ-1),易求得=(1,-1,-1).∵异面直线PQ与AD成30°角,∴cos 30°===,∴18λ2+2=-5q2+16q.∵0≤q<1,∴-5q2+16q∈[0,11),即解得-<λ<.∵0<λ≤1,∴0<λ<,可得||==λ∈(0,1).故选C.
4.D 如图,构造长方体ABCD-PQGH,则E是GH的中点.
在A中,∵二面角D-BC-G是直二面角,
∴二面角D-BC-E是锐二面角,故A错误;
在B中,连接BD,MN,则N是BD的中点,
∴MN∥BE,
∴BM与EN是相交直线,故B错误;
在C中,以C为原点,CD所在直线为x轴,CB所在直线为y轴,CG所在直线为z轴,建立如图所示的空间直角坐标系,
设AB=2,
则C(0,0,0),B(0,2,0),D(2,0,0),E(1,0,),M,N(1,1,0),
∴=,=(0,1,-),
∴·=-≠0,∴CM与EN不垂直,故C错误;
在D中,=(0,1,-),=,=(0,2,0),
设平面MCB的一个法向量为n=(x,y,z),
则
令x=1,得n=(1,0,-),
设直线EN与平面MCB所成的角为θ,
则sin θ==,
∴直线EN与平面MCB所成角的正弦值为,故D正确.故选D.
5.ABD 根据题意,得·=·=·=1×1×cos 60°=,所以(++)2=+++2(·+·+·)=3+3=6,
2=2(+)2=2(++2·)=2×(1+1+1)=6,故A正确;
由=+-,=+,得||===,||==,
·=(+-)·(+)=+·+·-=1,
所以cos<,>==,故B正确;
连接BD交AC于点O.易知四面体A1-ABD为正四面体,则点A1在平面ABD上的射影P为AO上靠近O的三等分点,则AP=AO=,
∴cos∠A1AP=,即AA1与平面ABCD所成角的余弦值为,故C错误;
因为A1D1∥平面ABCD,所以A1D1到平面ABCD的距离d即为点A1到平面ABCD的距离,所以d=PA1==,故D正确.
6.答案 -
解析 不妨设||=||=||=||=1,由题意知,向量,,不共面,α≠90°,α≠0°,所以存在实数a,b,c使得=a+b+c,
则·=a·+b·+c·,
所以=a||||cos α+b||||cos α+c||||cos α,
所以1=acos α+bcos α+ccos α,即a+b+c=.
因为·=a+b·+c·,
所以||||cos α=a+b||||cos α+c||·|OA|cos α,
所以cos α=a+bcos α+ccos α,即a=(1-b-c)cos α,
同理可得b=(1-a-c)cos α,c=(1-a-b)cos α,
所以a+b+c=cos α=,
所以3cos2α-2cos α-1=0,
所以cos α=-或cos α=1(舍去).
7.解析 以A为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2),∴=(0,2,0),=(1,1,-2),=(0,2,-2),=(-1,0,2),=(-1,1,0),=(0,-1,0).
(1)∵PA⊥平面ABCD,AD 平面ABCD,
∴PA⊥AD,又AB⊥AD,PA∩AB=A,
∴AD⊥平面PAB,
∴=(0,2,0)是平面PAB的一个法向量.
设平面PCD的一个法向量为m=(x,y,z),
则即令y=1,则z=1,x=1,
∴m=(1,1,1),
∴cos< ,m>==,∴平面PAB与平面PCD所成锐二面角的余弦值为.
(2)设Q为直线PB上一点, =λ =(-λ,0,2λ)(λ∈R),
又 =(-1,1,0), =(0,-1,0),
∴ = + =(-λ,-1,2λ),则点Q到直线CD的距离d=
=
=
==≥,
故异面直线PB与CD之间的距离为.
8.解析 (1)证明:在题图1中,AF=FC,BF+FC=AB,设AB=a(a>0),BF=x(x>0),则BC=3a,
在△BAF中,BF2+AB2=AF2,即x2+3a2=(3a-x)2,
解得x=a,则AF=FC=2BF=2a,所以∠BAF=30°,易知△EFC为等边三角形,所以EF=EC.
因为在题图2中,点B落在线段FC上,所以BC=BF=a,所以BE⊥FC,
又AB⊥BF,即AB⊥CF,AB∩BE=B,AB,BE 平面ABE,所以CF⊥平面ABE.
又CF 平面EFC,所以平面ABE⊥平面EFC.
(2)以F为原点,FC所在直线为x轴,过点F且平行于BE的直线为y轴,过点F且垂直于平面EFC的直线为z轴,建立如图所示的空间直角坐标系,
则F(0,0,0),C(2a,0,0),B(a,0,0),E(a,a,0),所以=(0,a,0),
易得平面ABE的一个法向量为=(2a,0,0).
过D作DG⊥EC于G, 因为平面DEC⊥平面EFC,所以DG⊥平面EFC,
则D,所以=.
设平面DBE的一个法向量为n=(x,y,z),
则
令z=,则y=0,x=-6,所以n=(-6,0,).
因为cos===,
所以锐二面角A-BE-D的正弦值为=.
9.解析 (1)证明:取BC的中点E,连接DE,如图.
设AB=AD=a,则BC=2a,
依题意得,四边形ABED为正方形,则BE=DE=CE=a,BD=CD=a,
所以BD2+CD2=BC2,所以BD⊥CD.
又平面SCD⊥平面ABCD,平面SCD∩平面ABCD=CD,BD 平面ABCD,所以BD⊥平面SCD.
又BD 平面MBD,所以平面MBD⊥平面SCD.
(2)假设存在点M,使得二面角A-BD-M的余弦值为,过点S作CD的垂线,交CD的延长线于点H,连接AH,如图.
因为平面SCD⊥平面ABCD,平面SCD∩平面ABCD=CD,SH⊥CD,SH 平面SCD,所以SH⊥平面ABCD,故DH为斜线SD在平面ABCD内的射影,∠SDH为斜线SD与平面ABCD所成的角,即∠SDH=60°.
在Rt△SHD中,SD=CD=a,
所以DH=a,SH=a,
在△ADH中,∠ADH=45°,AD=a,DH=a,
所以∠AHD=90°,AH=a.
过点D作DF∥SH,则DF⊥平面ABCD,
所以DB,DC,DF两两垂直.
以D为坐标原点,的方向为x轴正方向,的方向为y轴正方向,的方向为z轴正方向,建立空间直角坐标系,
则D(0,0,0),B(a,0,0),S,A,
故=,=0,-a,a,=(a,0,0).
设=λ=λ=(0≤λ≤1),
所以=+=.
设平面MBD的一个法向量为n=(x,y,z),
则即
令z=1,可得n=(0,-λ,1).
易知平面ABD的一个法向量为m=(0,0,1),
所以|cos|===,解得λ=或λ=(舍去),
所以当M是棱SA的中点时,二面角A-BD-M的余弦值为.
综合拔高练
五年高考练
考点1 用空间向量判断线面位置关系
1.(2021新高考Ⅰ,12)在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则( )
A.当λ=1时,△AB1P的周长为定值
B.当μ=1时,三棱锥P-A1BC的体积为定值
C.当λ=时,有且仅有一个点P,使得A1P⊥BP
D.当μ=时,有且仅有一个点P,使得A1B⊥平面AB1P
2.(2019江苏,16)如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:
(1)A1B1∥平面DEC1;
(2)BE⊥C1E.
考点2 用空间向量求空间中的角
3.(2017课标全国Ⅲ理,16)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是 .(填写所有正确结论的编号)
4.(2021浙江,19)如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC=4,PA=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.
(1)证明:AB⊥PM;
(2)求直线AN与平面PDM所成角的正弦值.
5.(2020新高考Ⅰ,20)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
6.(2021新高考Ⅰ,20)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.
(1)证明:OA⊥CD;
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.
考点3 利用空间向量求空间中的距离
7.(2019课标全国Ⅰ文,19)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
考点4 用空间向量解决探究性问题
8.(2021全国甲,19)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
(1)证明:BF⊥DE;
(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小
三年模拟练
应用实践
1.(2022河北石家庄第十七中学月考)现有以下命题:①若a∥b,则存在唯一的实数λ,使得a=λb;②若a·b=b·c,则a=c或b=0;③若{a,b,c}为空间向量的一组基底,则{a+b,b+c,c+a}构成空间向量的另一组基底;④(a·b)·(c·d)=(d·c)·(b·a)一定成立.其中真命题的个数为( )
A.4 B.3 C.2 D.1
2.(2022广东广州第七中学检测)已知三棱锥S-ABC中,SA=SB=SC=1,且SA,SB,SC两两垂直,P是三棱锥S-ABC外接球面上一动点,则点P到平面ABC的距离的最大值是( )
A. B. C. D.
3.(2021江苏常州中学高二期中)如图,在三棱锥A-BCD中,平面ABC⊥平面BCD,△BAC与△BCD均为直角三角形,且∠BAC=∠BCD=90°,AB=AC,CD=BC=1,点P是线段AB上的动点,若线段CD上存在点Q,使得异面直线PQ与AD成30°角,则线段PA的长的取值范围是( )
A. B.
C.(0,1) D.(0,]
4.(2020安徽合肥一六八中学段考)如图,N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则下列结论正确的是( )
A.二面角D-BC-E是直二面角
B.直线BM,EN是异面直线
C.CM⊥EN
D.直线EN与平面MCB所成角的正弦值为
5.(多选)(2022浙江杭州高级中学月考)如图,一个结晶体的形状为平行六面体ABCD-A1B1C1D1,其中,以顶点A为端点的三条棱长都等于1,且它们彼此的夹角都是60°,下列说法中正确的是( )
A.(++)2=2
B.BD1与AC所成角的余弦值为
C.AA1与平面ABCD所成角的余弦值为
D.A1D1到平面ABCD的距离为
6.(2022北京大兴第一中学检测)在空间中,四个不共线的向量,,,两两间的夹角均为α,则cos α的大小为 .
7.(2022山东平邑第一中学期中)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,∠ABC=∠BAD=,PA=AD=2,AB=BC=1.
(1)求平面PAB与平面PCD所成锐二面角的余弦值;
(2)定义两条异面直线之间的距离为其中一条直线上任意一点到另一条直线距离的最小值,利用此定义求异面直线PB与CD之间的距离.
8.如图1,在矩形ABCD中,AB=BC,将矩形ABCD折起,使点A与点C重合,折痕为EF,展开后连接AF,CE,以AF和EF为折痕,将四边形ABFE折起,使点B落在线段FC上,将△CDE向上折起,使平面DEC⊥平面EFC,如图2.
(1)证明:平面ABE⊥平面EFC;
(2)求锐二面角A-BE-D的正弦值.
9.(2021江苏镇江第一中学期末)如图,四棱锥S-ABCD的底面ABCD是直角梯形,∠ABC=90°,AD∥BC,侧面△SCD为钝角三角形,CD=SD,平面SCD⊥平面ABCD,M是棱SA上的动点,AB=AD=BC.
(1)求证:平面MBD⊥平面SCD;
(2)若直线SD与底面ABCD所成的角为60°,是否存在点M使得二面角A-BD-M的余弦值为 若存在,确定点M的位置;若不存在,请说明理由.
答案与分层梯度式解析
第一章 空间向量与立体几何
综合拔高练
五年高考练
1.BD 选项A,当λ=1时,点P在线段CC1上,设CP=x(0≤x≤1),若x=0,则△AB1P即为△AB1C,此时△AB1P的周长为2+1;若x=1,则△AB1P即为△AB1C1,此时△AB1P的周长为2+1.若0
在Rt△B1C1P中,PB1==,
而AB1=,所以△AB1P的周长为++,不为定值,故选项A错误;
选项B,当μ=1时,点P在线段B1C1上,
因为B1C1∥BC,B1C1 平面A1BC,BC 平面A1BC,
所以B1C1∥平面A1BC,
所以直线B1C1上的任何一点到平面A1BC的距离均相等,
所以三棱锥P-A1BC的体积为定值,故选项B正确;
取BC,B1C1的中点分别为O,O1,连接OO1,AO,易知OO1⊥平面ABC,AO⊥BC,以OB,OA,OO1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则B,A,A1,选项C,当λ=时,点P在线段OO1上,设P(0,0,z)(0≤z≤1),则=,=,若A1P⊥BP,则·=0,
即z(z-1)=0,解得z=0或z=1,即当λ=时,存在两个点P,使得A1P⊥BP,故选项C错误;
选项D,当μ=时,点P在线段MN上(M,N分别是线段BB1,CC1的中点),
设P,则=,
若A1B⊥平面AB1P,则A1B⊥AP,则·=0,
即·=x+-=0,解得x=-,所以P,易验证此时满足A1B⊥平面AB1P,
所以当μ=时,有且仅有一个点P,使得A1B⊥平面AB1P,故选项D正确.故选BD.
2.证明 (1)取A1C1的中点E1,连接EE1.
由题易得,EC,EB,EE1两两垂直,以E为原点,EC,EB,EE1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图.
设AC=2c,AB=b,AA1=a(c>0,a>0),
则E(0,0,0),B(0,,0),D,A1(-c,0,a),B1(0,,a),C1(c,0,a),
所以=(c,,0),=,
所以=2,所以∥,
所以A1B1∥ED.
因为ED 平面DEC1,A1B1 平面DEC1,
所以A1B1∥平面DEC1.
(2)由(1)得=(0,,0),=(c,0,a),
而·=0,所以⊥,
所以BE⊥C1E.
3.答案 ②③
解析 过点C作直线a1∥a,b1∥b,则直线AC,a1,b1两两垂直.不妨分别以a1,b1,AC所在直线为x轴、y轴、z轴建立空间直角坐标系,取n1=(1,0,0)为a1的方向向量,n2=(0,1,0)为b1的方向向量,令A(0,0,1).可设B(cos θ,sin θ,0),则=(cos θ,sin θ,-1).
当直线AB与a成60°角时,|cos
∴|cos θ|=,|sin θ|=,
∴|cos
即AB与b所成角也是60°.
∵|cos
∴直线AB与a所成角的最小值为45°.
综上,②和③是正确的,①和④是错误的.
4.解析 (1)证明:在△CDM中,DC=1,MC=2,∠DCM=60°,则DM=,所以CD⊥DM.
又因为CD⊥PD,所以CD⊥平面PDM.
因此CD⊥PM.
又因为AB∥CD,所以AB⊥PM.
(2)如图,以D为原点,分别以射线DM,DC为x轴,y轴的正半轴,建立空间直角坐标系Dxyz.
则A(2,-2,0),C(0,1,0),M(,0,0),设P(,0,z0),z0>0,
因为PA=,所以z0=2,
故P(,0,2),N,
所以=,=(,0,2),=(,0,0).
设平面PDM的一个法向量为n=(x,y,z),
由得取n=(0,1,0).
设直线AN与平面PDM所成角为α,
所以sin α=|cos<,n>|==.
因此,直线AN与平面PDM所成角的正弦值为.
5.解析 (1)证明:因为PD⊥底面ABCD,所以PD⊥AD.又底面ABCD为正方形,所以AD⊥DC.因此AD⊥平面PDC.
因为AD∥BC,AD 平面PBC,
所以AD∥平面PBC.
由已知得l∥AD.因此l⊥平面PDC.
(2)以D为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系Dxyz,则D(0,0,0),C(0,1,0),B(1,1,0),P(0,0,1),=(0,1,0),=(1,1,-1).
由(1)可设Q(a,0,1),则=(a,0,1).
设n=(x,y,z)是平面QCD的一个法向量,则
即可取n=(-1,0,a).
所以cos
设PB与平面QCD所成的角为θ,
则sin θ=×=.
因为≤,当且仅当a=1时等号成立,所以PB与平面QCD所成角的正弦值的最大值为.
6.解析 (1)证明:在△ABD中,∵AB=AD,O为BD的中点,∴AO⊥BD,又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO 平面ABD,∴AO⊥平面BCD,又CD 平面BCD,∴AO⊥CD.
(2)由OC=OD=OB得BC⊥CD,由(1)知AO⊥平面BCD,以C为原点,,,的方向分别为x轴、y轴、z轴正方向建立空间直角坐标系,如图所示,则C(0,0,0),B(0,,0),设AO=a.
则E,∴=(0,,0),=,设平面EBC的法向量为n=(x,y,z),则即令x=a,则z=-1,∴n=(a,0,-1),
易知平面BCD的一个法向量为m=(0,0,1),
由题可知|cos
∴VA-BCD=S△BCD·AO=××1××1=,
故三棱锥A-BCD的体积为.
7.解析 (1)证明:∵直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点,
∴DD1⊥平面ABCD,DE⊥AD,
以D为原点,DA,DE,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,
则M(1,,2),N(1,0,2),D(0,0,0),E(0,,0),C1(-1,,4),∴=(0,-,0),=(-1,,4),=(0,,0),
设平面C1DE的一个法向量为n=(x,y,z),
则即
取z=1,则n=(4,0,1).
∵·n=0,MN 平面C1DE,
∴MN∥平面C1DE.
(2)由(1)得C(-1,,0),∴=(-1,,0),
而平面C1DE的一个法向量为n=(4,0,1),
∴点C到平面C1DE的距离d===.
8.解析 ∵BF⊥A1B1,B1B⊥A1B1,BF∩B1B=B,
∴A1B1⊥平面B1C1CB,∵AB∥A1B1,∴AB⊥平面B1C1CB,
又∵BC 平面B1C1CB,∴AB⊥BC.
以B为坐标原点,BA,BC,BB1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则B(0,0,0),F(0,2,1),E(1,1,0),∴=(0,2,1),设B1D=a(0≤a≤2),则D(a,0,2),则=(1-a,1,-2).
(1)证明:∵·=(0,2,1)·(1-a,1,-2)=0×(1-a)+2×1+1×(-2)=0,∴BF⊥DE.
(2)=(-1,1,1),=(a,-2,1),
设平面DFE的法向量为n=(x,y,z),
则
不妨设x=1,则y=,z=,∴n=.
易知m=(1,0,0)是平面BB1C1C的一个法向量.
设平面BB1C1C与平面DEF所成的锐二面角的大小为θ,
则cos θ=|cos
∴sin θ=≥,故当a=,即B1D=时,平面BB1C1C与平面DFE所成的二面角的正弦值最小,最小值为.
三年模拟练
1.C 当b=0时,①显然不成立,
当a⊥b,且b⊥c时,a·b=b·c=0,不能说明a=c或b=0,故②错误;
若{a,b,c}为空间向量的一组基底,则a,b,c不共面,所以a+b,b+c,c+a也不共面,则{a+b,b+c,c+a}构成空间向量的另一组基底,故③正确;
因为a·b=b·a,c·d=d·c,所以(a·b)·(c·d)=(d·c)·(b·a),故④正确.
2.C ∵SA,SB,SC两两垂直,且SA=SB=SC=1,∴以SA,SB,SC为棱长补作正方体MNQB-ADCS,如图.以B为原点,BM,BQ,BS所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则B(0,0,0),A(1,0,1),C(0,1,1),N(1,1,0),∴=(1,0,1),=(0,1,1),=(1,1,0).
设平面ABC的一个法向量为n=(x,y,z),
则取x=1,则y=1,z=-1,∴n=(1,1,-1),
三棱锥S-ABC的外接球就是棱长为1的正方体MNQB-ADCS的外接球.
∵点P是三棱锥S-ABC外接球面上一动点,
∴由正方体与球的几何性质可得,当点P与点N重合时,点P到平面ABC的距离最大,
∴点P到平面ABC的距离的最大值为==.
3.C 如图,以C为原点,CD所在直线为x轴,CB所在直线为y轴,过C且与平面BCD垂直的直线为z轴,建立空间直角坐标系,则C(0,0,0),A(0,1,1),B(0,2,0),D(1,0,0),设Q(q,0,0)(0≤q<1),设=λ=(0,λ,-λ)(0<λ≤1),则=-(+)=(q,0,0)-(0,1,1)-(0,λ,-λ)=(q,-1-λ,λ-1),易求得=(1,-1,-1).∵异面直线PQ与AD成30°角,∴cos 30°===,∴18λ2+2=-5q2+16q.∵0≤q<1,∴-5q2+16q∈[0,11),即解得-<λ<.∵0<λ≤1,∴0<λ<,可得||==λ∈(0,1).故选C.
4.D 如图,构造长方体ABCD-PQGH,则E是GH的中点.
在A中,∵二面角D-BC-G是直二面角,
∴二面角D-BC-E是锐二面角,故A错误;
在B中,连接BD,MN,则N是BD的中点,
∴MN∥BE,
∴BM与EN是相交直线,故B错误;
在C中,以C为原点,CD所在直线为x轴,CB所在直线为y轴,CG所在直线为z轴,建立如图所示的空间直角坐标系,
设AB=2,
则C(0,0,0),B(0,2,0),D(2,0,0),E(1,0,),M,N(1,1,0),
∴=,=(0,1,-),
∴·=-≠0,∴CM与EN不垂直,故C错误;
在D中,=(0,1,-),=,=(0,2,0),
设平面MCB的一个法向量为n=(x,y,z),
则
令x=1,得n=(1,0,-),
设直线EN与平面MCB所成的角为θ,
则sin θ==,
∴直线EN与平面MCB所成角的正弦值为,故D正确.故选D.
5.ABD 根据题意,得·=·=·=1×1×cos 60°=,所以(++)2=+++2(·+·+·)=3+3=6,
2=2(+)2=2(++2·)=2×(1+1+1)=6,故A正确;
由=+-,=+,得||===,||==,
·=(+-)·(+)=+·+·-=1,
所以cos<,>==,故B正确;
连接BD交AC于点O.易知四面体A1-ABD为正四面体,则点A1在平面ABD上的射影P为AO上靠近O的三等分点,则AP=AO=,
∴cos∠A1AP=,即AA1与平面ABCD所成角的余弦值为,故C错误;
因为A1D1∥平面ABCD,所以A1D1到平面ABCD的距离d即为点A1到平面ABCD的距离,所以d=PA1==,故D正确.
6.答案 -
解析 不妨设||=||=||=||=1,由题意知,向量,,不共面,α≠90°,α≠0°,所以存在实数a,b,c使得=a+b+c,
则·=a·+b·+c·,
所以=a||||cos α+b||||cos α+c||||cos α,
所以1=acos α+bcos α+ccos α,即a+b+c=.
因为·=a+b·+c·,
所以||||cos α=a+b||||cos α+c||·|OA|cos α,
所以cos α=a+bcos α+ccos α,即a=(1-b-c)cos α,
同理可得b=(1-a-c)cos α,c=(1-a-b)cos α,
所以a+b+c=cos α=,
所以3cos2α-2cos α-1=0,
所以cos α=-或cos α=1(舍去).
7.解析 以A为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2),∴=(0,2,0),=(1,1,-2),=(0,2,-2),=(-1,0,2),=(-1,1,0),=(0,-1,0).
(1)∵PA⊥平面ABCD,AD 平面ABCD,
∴PA⊥AD,又AB⊥AD,PA∩AB=A,
∴AD⊥平面PAB,
∴=(0,2,0)是平面PAB的一个法向量.
设平面PCD的一个法向量为m=(x,y,z),
则即令y=1,则z=1,x=1,
∴m=(1,1,1),
∴cos< ,m>==,∴平面PAB与平面PCD所成锐二面角的余弦值为.
(2)设Q为直线PB上一点, =λ =(-λ,0,2λ)(λ∈R),
又 =(-1,1,0), =(0,-1,0),
∴ = + =(-λ,-1,2λ),则点Q到直线CD的距离d=
=
=
==≥,
故异面直线PB与CD之间的距离为.
8.解析 (1)证明:在题图1中,AF=FC,BF+FC=AB,设AB=a(a>0),BF=x(x>0),则BC=3a,
在△BAF中,BF2+AB2=AF2,即x2+3a2=(3a-x)2,
解得x=a,则AF=FC=2BF=2a,所以∠BAF=30°,易知△EFC为等边三角形,所以EF=EC.
因为在题图2中,点B落在线段FC上,所以BC=BF=a,所以BE⊥FC,
又AB⊥BF,即AB⊥CF,AB∩BE=B,AB,BE 平面ABE,所以CF⊥平面ABE.
又CF 平面EFC,所以平面ABE⊥平面EFC.
(2)以F为原点,FC所在直线为x轴,过点F且平行于BE的直线为y轴,过点F且垂直于平面EFC的直线为z轴,建立如图所示的空间直角坐标系,
则F(0,0,0),C(2a,0,0),B(a,0,0),E(a,a,0),所以=(0,a,0),
易得平面ABE的一个法向量为=(2a,0,0).
过D作DG⊥EC于G, 因为平面DEC⊥平面EFC,所以DG⊥平面EFC,
则D,所以=.
设平面DBE的一个法向量为n=(x,y,z),
则
令z=,则y=0,x=-6,所以n=(-6,0,).
因为cos
所以锐二面角A-BE-D的正弦值为=.
9.解析 (1)证明:取BC的中点E,连接DE,如图.
设AB=AD=a,则BC=2a,
依题意得,四边形ABED为正方形,则BE=DE=CE=a,BD=CD=a,
所以BD2+CD2=BC2,所以BD⊥CD.
又平面SCD⊥平面ABCD,平面SCD∩平面ABCD=CD,BD 平面ABCD,所以BD⊥平面SCD.
又BD 平面MBD,所以平面MBD⊥平面SCD.
(2)假设存在点M,使得二面角A-BD-M的余弦值为,过点S作CD的垂线,交CD的延长线于点H,连接AH,如图.
因为平面SCD⊥平面ABCD,平面SCD∩平面ABCD=CD,SH⊥CD,SH 平面SCD,所以SH⊥平面ABCD,故DH为斜线SD在平面ABCD内的射影,∠SDH为斜线SD与平面ABCD所成的角,即∠SDH=60°.
在Rt△SHD中,SD=CD=a,
所以DH=a,SH=a,
在△ADH中,∠ADH=45°,AD=a,DH=a,
所以∠AHD=90°,AH=a.
过点D作DF∥SH,则DF⊥平面ABCD,
所以DB,DC,DF两两垂直.
以D为坐标原点,的方向为x轴正方向,的方向为y轴正方向,的方向为z轴正方向,建立空间直角坐标系,
则D(0,0,0),B(a,0,0),S,A,
故=,=0,-a,a,=(a,0,0).
设=λ=λ=(0≤λ≤1),
所以=+=.
设平面MBD的一个法向量为n=(x,y,z),
则即
令z=1,可得n=(0,-λ,1).
易知平面ABD的一个法向量为m=(0,0,1),
所以|cos
所以当M是棱SA的中点时,二面角A-BD-M的余弦值为.
