2022—2023学年人教版数学九年级上册24.3正多边形和圆 课件(共14张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册24.3正多边形和圆 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 16:36:21 | ||
图片预览


文档简介
(共14张PPT)
24.3 正多边形和圆
图片欣赏
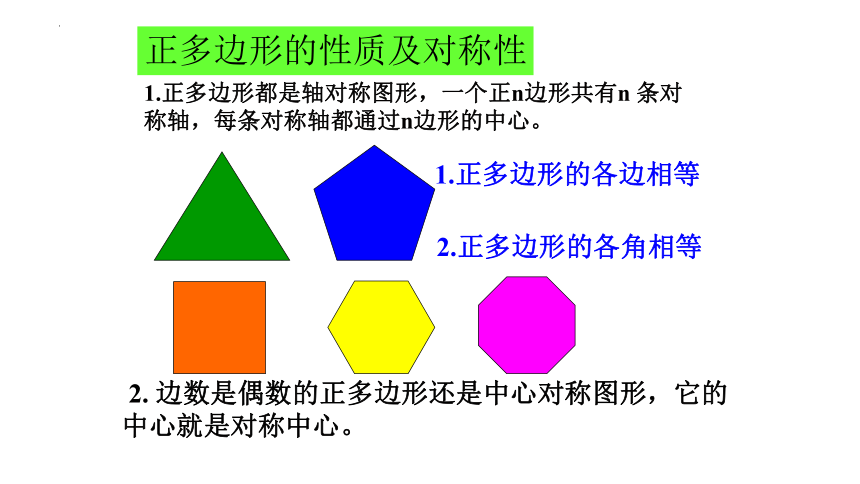
1.正多边形都是轴对称图形,一个正n边形共有n 条对称轴,每条对称轴都通过n边形的中心。
正多边形的性质及对称性
2. 边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。
1.正多边形的各边相等
2.正多边形的各角相等
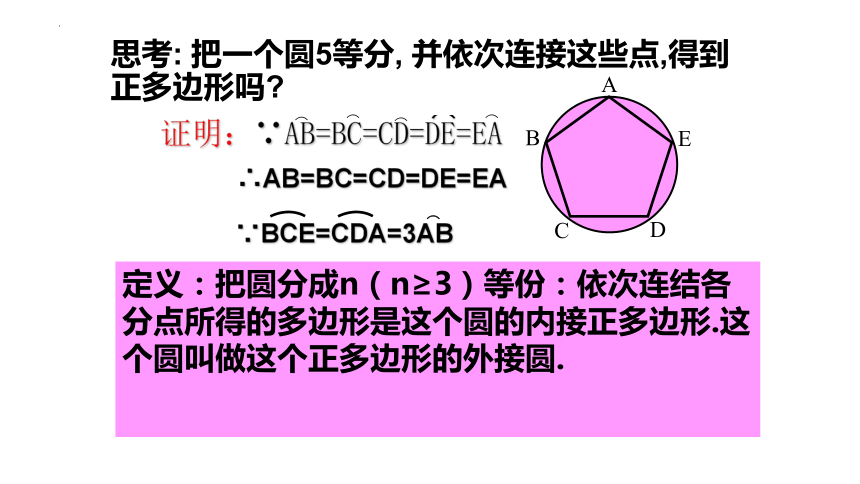
思考: 把一个圆5等分, 并依次连接这些点,得到正多边形吗
证明:∵AB=BC=CD=DE=EA
A
B
C
D
E
⌒
⌒
⌒
⌒
⌒
∴AB=BC=CD=DE=EA
∵BCE=CDA=3AB
⌒
∴∠A=∠B
同理∠B=∠C=∠D=∠E
∴∠A=∠B=∠C=∠D=∠E
又∵顶点A、B、C、D、E都在⊙O上
∴五边形ABCDE是⊙O的 内接正五边形.
定义:把圆分成n(n≥3)等份:依次连结各分点所得的多边形是这个圆的内接正多边形.这个圆叫做这个正多边形的外接圆.
⌒
⌒
⌒
1
2
3
A
B
C
D
E
4
⌒
⌒
5
弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的内角相等)
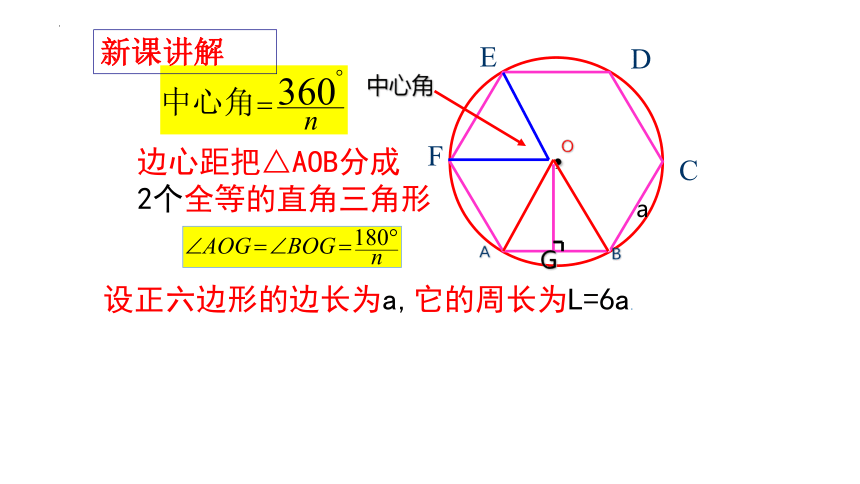
新课讲解
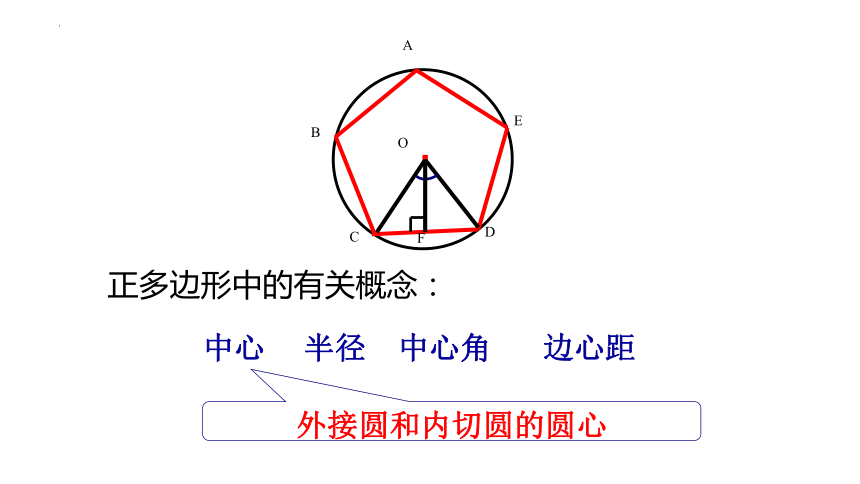
中心
E
D
C
B
A
O
半径
中心角
边心距
正多边形中的有关概念:
F
外接圆和内切圆的圆心
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正六边形的边长为a,它的周长为L=6a.
a
新课讲解
E
D
C
B
A
O
F
中心角与内角互补
正n边形的一个内角的
度数是____________;
中心角是___________;
正多边形的中心角与外角的大小关系是________.
相等
新课讲解
正多边形边数 每个内角 中心角
3
4
6
8
10
12
135°
120°
90°
90°
120°
60°
60°
45°
144°
36°
150°
30°
例2 如图29-5-4,△ABC为⊙O的内接正三角形.如果的⊙O半径为r,求这个正三角形的边长和边心距.
解:如图29-5-5,连接OB,过点O作OD⊥BC,垂足为D.在Rt△OBD中,
∵∠OBD=30°,OB=r,
∴OD= ,BD= ,BC=2BD= .
即这个正三角形的边长为 ,边心距为 .
正多边形边数 边长 半径 边心距 中心角
3
4
6
(1)正 n 边形的半径和边心距把正 n 边形分成___
个全等的直角三角形;
(2)正三角形的半径为 R,则边长为_____,边心
距为______,面积为________.若正三角形边长为 a,
则半径为______;
(3)正 n 边形的一个外角为 30°,则它的边数为
____,它的内角和为______;
(4)如果一个正多边形的一个外角等于一个内角
的三分之二,则这个正多边形的边数 n =____;
4.强化练习
(5)正六边形的边长为 1,则它的半径为_____,
面积为________;
(6)同圆的内接正三角形、正方形、正六边形的
边长之比为________________;
(7)正三角形的高∶半径∶边心距为_________;
(8)边长为 1 的正六边形的内切圆的面积是____.
4.强化练习
小结
1.正多边形中的有关概念;
2.正多边形的对称性;
3.正多边形中的有关计算:
中心角 = _____
=外角
内角= ___________
边长、半径、边心距知一求二
1
2
l r
面积S=
24.3 正多边形和圆
图片欣赏
1.正多边形都是轴对称图形,一个正n边形共有n 条对称轴,每条对称轴都通过n边形的中心。
正多边形的性质及对称性
2. 边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。
1.正多边形的各边相等
2.正多边形的各角相等
思考: 把一个圆5等分, 并依次连接这些点,得到正多边形吗
证明:∵AB=BC=CD=DE=EA
A
B
C
D
E
⌒
⌒
⌒
⌒
⌒
∴AB=BC=CD=DE=EA
∵BCE=CDA=3AB
⌒
∴∠A=∠B
同理∠B=∠C=∠D=∠E
∴∠A=∠B=∠C=∠D=∠E
又∵顶点A、B、C、D、E都在⊙O上
∴五边形ABCDE是⊙O的 内接正五边形.
定义:把圆分成n(n≥3)等份:依次连结各分点所得的多边形是这个圆的内接正多边形.这个圆叫做这个正多边形的外接圆.
⌒
⌒
⌒
1
2
3
A
B
C
D
E
4
⌒
⌒
5
弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的内角相等)
新课讲解
中心
E
D
C
B
A
O
半径
中心角
边心距
正多边形中的有关概念:
F
外接圆和内切圆的圆心
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正六边形的边长为a,它的周长为L=6a.
a
新课讲解
E
D
C
B
A
O
F
中心角与内角互补
正n边形的一个内角的
度数是____________;
中心角是___________;
正多边形的中心角与外角的大小关系是________.
相等
新课讲解
正多边形边数 每个内角 中心角
3
4
6
8
10
12
135°
120°
90°
90°
120°
60°
60°
45°
144°
36°
150°
30°
例2 如图29-5-4,△ABC为⊙O的内接正三角形.如果的⊙O半径为r,求这个正三角形的边长和边心距.
解:如图29-5-5,连接OB,过点O作OD⊥BC,垂足为D.在Rt△OBD中,
∵∠OBD=30°,OB=r,
∴OD= ,BD= ,BC=2BD= .
即这个正三角形的边长为 ,边心距为 .
正多边形边数 边长 半径 边心距 中心角
3
4
6
(1)正 n 边形的半径和边心距把正 n 边形分成___
个全等的直角三角形;
(2)正三角形的半径为 R,则边长为_____,边心
距为______,面积为________.若正三角形边长为 a,
则半径为______;
(3)正 n 边形的一个外角为 30°,则它的边数为
____,它的内角和为______;
(4)如果一个正多边形的一个外角等于一个内角
的三分之二,则这个正多边形的边数 n =____;
4.强化练习
(5)正六边形的边长为 1,则它的半径为_____,
面积为________;
(6)同圆的内接正三角形、正方形、正六边形的
边长之比为________________;
(7)正三角形的高∶半径∶边心距为_________;
(8)边长为 1 的正六边形的内切圆的面积是____.
4.强化练习
小结
1.正多边形中的有关概念;
2.正多边形的对称性;
3.正多边形中的有关计算:
中心角 = _____
=外角
内角= ___________
边长、半径、边心距知一求二
1
2
l r
面积S=
同课章节目录
