2022-2023学年人教版九年级数学上册25.1.2 概率 课件 (共17张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册25.1.2 概率 课件 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 07:18:49 | ||
图片预览






文档简介
(共17张PPT)
25.1.2 概率
瓮中捉鳖
请用数学的思维和眼光描述 :
守株待兔
拔苗助长
不可能事件
必然事件
随机事件
抛掷一枚质地均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
反面朝上
掷硬币
请问:正面朝上和反面朝上的
可能性大小相同吗
思考:
掷一枚质地均匀的骰子,掷到结果有多少种?
掷骰子
请问:每个点数被掷到的
可能性大小相同吗?
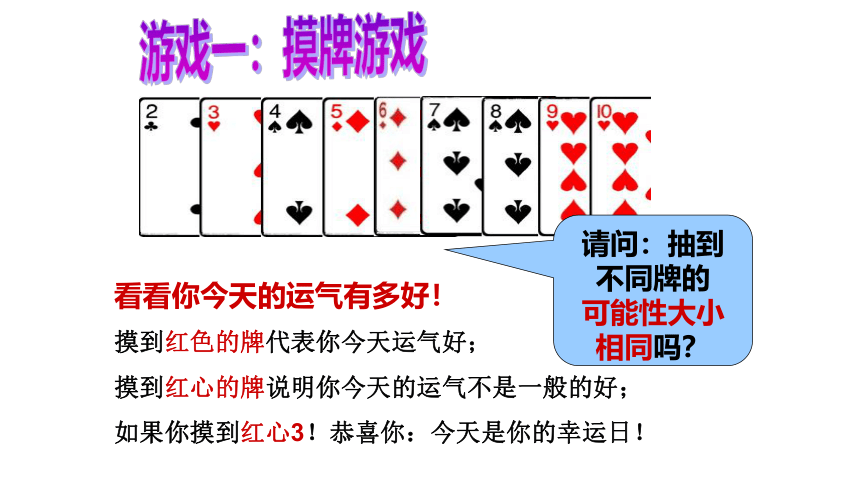
游戏一:摸牌游戏
看看你今天的运气有多好!
摸到红色的牌代表你今天运气好;
摸到红心的牌说明你今天的运气不是一般的好;
如果你摸到红心3!恭喜你:今天是你的幸运日!
请问:抽到不同牌的
可能性大小相同吗?
节日上的"套圈"游戏
你认为套中不同东西的可能性大小相同吗
小红生病了,需要动手术,父母很担心,但当听到手术有百分之九十九的成功率的时候,父母松了一口气,放心了不少!
小明得了很严重的病,动手术只有千分之一的成功率,父母很担心!
千分之一的成功率
百分之九十九的成功率
用数值表示随机事件发生的可能性大小。
概率
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记为P(A).
1.概率的定义:
概率从数量上刻画了一个随机事件发生的可能性大小。
实验1:掷一枚硬币,落地后
(1)会出现几种可能的结果?
(2)正面朝上与反面朝上的可能性会相等吗?
(3)试猜想:正面朝上的可能性有多大呢?
开始
正面朝上
反面朝上
两种
实验2:抛掷一个质地均匀的骰子
(1)它落地时向上的点数有几种可能的结果?
(2)各点数出现的可能性会相等吗?
(3)试猜想:你能用一个数值来说明各点数 出现的可能性大小吗?
6种
相等
归纳
一般地,对于一个随机事件A,把刻画其发生可能性大小的数值,称之为随机事件A发生的概率。记为P(A)
共同特征: 1.每一次试验中,可能出现的结果只有有限个。2. 每一次试验中,各种结果出现的可能性相等。
概率从数量上刻画了一个随机事件发生的可能性的大小。
具有这些特点的试验称为古典概率.在这些试验中出现的事件为等可能事件.
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率 .
等可能事件概率的求法
1、当A是必然发生的事件时,P(A)是多少 ?
2、当A是不可能发生的事件时,P(A)是多少?
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
不可能事件,必然事件与随机事件的关系
想一想
必然事件发生的可能性是
100%
,P(A)=1;
不可能事件发生的可能性是
0;
P(A)= 0;
3、不确定事件发生的可能性是大于0而小于1的.
即随机事件的概率为
由定义可知:
(1)概率反映了随机事件发生的可能性的大小。事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0;
(2)必然事件的概率为1,不可能事件的概率为0.因此 .
(3)随机事件的概率为
例1.掷一枚骰子,观察向上的一面的点数,求下列事件的概率。
①点数为2.
P(点数为2)=
②点数为奇数。
P(点数为奇数)=
③点数大于2且小于5.
P(点数大于2且小于5)=
例1变式 掷1个质地均匀的正方体骰子,观察向上一面的点数,
(1)求掷得点数为2或4或6的概率;
(2)小明在做掷骰子的试验时,前五次都没掷得点数2,求他第六次掷得点数2的概率。
25.1.2 概率
瓮中捉鳖
请用数学的思维和眼光描述 :
守株待兔
拔苗助长
不可能事件
必然事件
随机事件
抛掷一枚质地均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
反面朝上
掷硬币
请问:正面朝上和反面朝上的
可能性大小相同吗
思考:
掷一枚质地均匀的骰子,掷到结果有多少种?
掷骰子
请问:每个点数被掷到的
可能性大小相同吗?
游戏一:摸牌游戏
看看你今天的运气有多好!
摸到红色的牌代表你今天运气好;
摸到红心的牌说明你今天的运气不是一般的好;
如果你摸到红心3!恭喜你:今天是你的幸运日!
请问:抽到不同牌的
可能性大小相同吗?
节日上的"套圈"游戏
你认为套中不同东西的可能性大小相同吗
小红生病了,需要动手术,父母很担心,但当听到手术有百分之九十九的成功率的时候,父母松了一口气,放心了不少!
小明得了很严重的病,动手术只有千分之一的成功率,父母很担心!
千分之一的成功率
百分之九十九的成功率
用数值表示随机事件发生的可能性大小。
概率
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记为P(A).
1.概率的定义:
概率从数量上刻画了一个随机事件发生的可能性大小。
实验1:掷一枚硬币,落地后
(1)会出现几种可能的结果?
(2)正面朝上与反面朝上的可能性会相等吗?
(3)试猜想:正面朝上的可能性有多大呢?
开始
正面朝上
反面朝上
两种
实验2:抛掷一个质地均匀的骰子
(1)它落地时向上的点数有几种可能的结果?
(2)各点数出现的可能性会相等吗?
(3)试猜想:你能用一个数值来说明各点数 出现的可能性大小吗?
6种
相等
归纳
一般地,对于一个随机事件A,把刻画其发生可能性大小的数值,称之为随机事件A发生的概率。记为P(A)
共同特征: 1.每一次试验中,可能出现的结果只有有限个。2. 每一次试验中,各种结果出现的可能性相等。
概率从数量上刻画了一个随机事件发生的可能性的大小。
具有这些特点的试验称为古典概率.在这些试验中出现的事件为等可能事件.
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率 .
等可能事件概率的求法
1、当A是必然发生的事件时,P(A)是多少 ?
2、当A是不可能发生的事件时,P(A)是多少?
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
不可能事件,必然事件与随机事件的关系
想一想
必然事件发生的可能性是
100%
,P(A)=1;
不可能事件发生的可能性是
0;
P(A)= 0;
3、不确定事件发生的可能性是大于0而小于1的.
即随机事件的概率为
由定义可知:
(1)概率反映了随机事件发生的可能性的大小。事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0;
(2)必然事件的概率为1,不可能事件的概率为0.因此 .
(3)随机事件的概率为
例1.掷一枚骰子,观察向上的一面的点数,求下列事件的概率。
①点数为2.
P(点数为2)=
②点数为奇数。
P(点数为奇数)=
③点数大于2且小于5.
P(点数大于2且小于5)=
例1变式 掷1个质地均匀的正方体骰子,观察向上一面的点数,
(1)求掷得点数为2或4或6的概率;
(2)小明在做掷骰子的试验时,前五次都没掷得点数2,求他第六次掷得点数2的概率。
同课章节目录
