2022-2023学年苏科版八年级数学上册1.1 全等图形 同步强化提优训练(Word版含答案)
文档属性
| 名称 | 2022-2023学年苏科版八年级数学上册1.1 全等图形 同步强化提优训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 566.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 17:15:00 | ||
图片预览



文档简介
2022-2023学年苏科版八年级数学上《1.1 全等图形》同步强化提优训练
(时间:90分钟 满分:120分)
一.选择题(30分)
1. 两个三角形全等是指这两个三角形的 ( )
A. 形状、大小和位置都相同 B. 形状、大小都相同,与位置没有关系
C. 形状相同,与大小和位置没有关系 D. 形状、大小和位置都没有关系
2、下列各选项中的两个图形属于全等形的是 ( )
3、下列图形中与已知图形全等的是( )
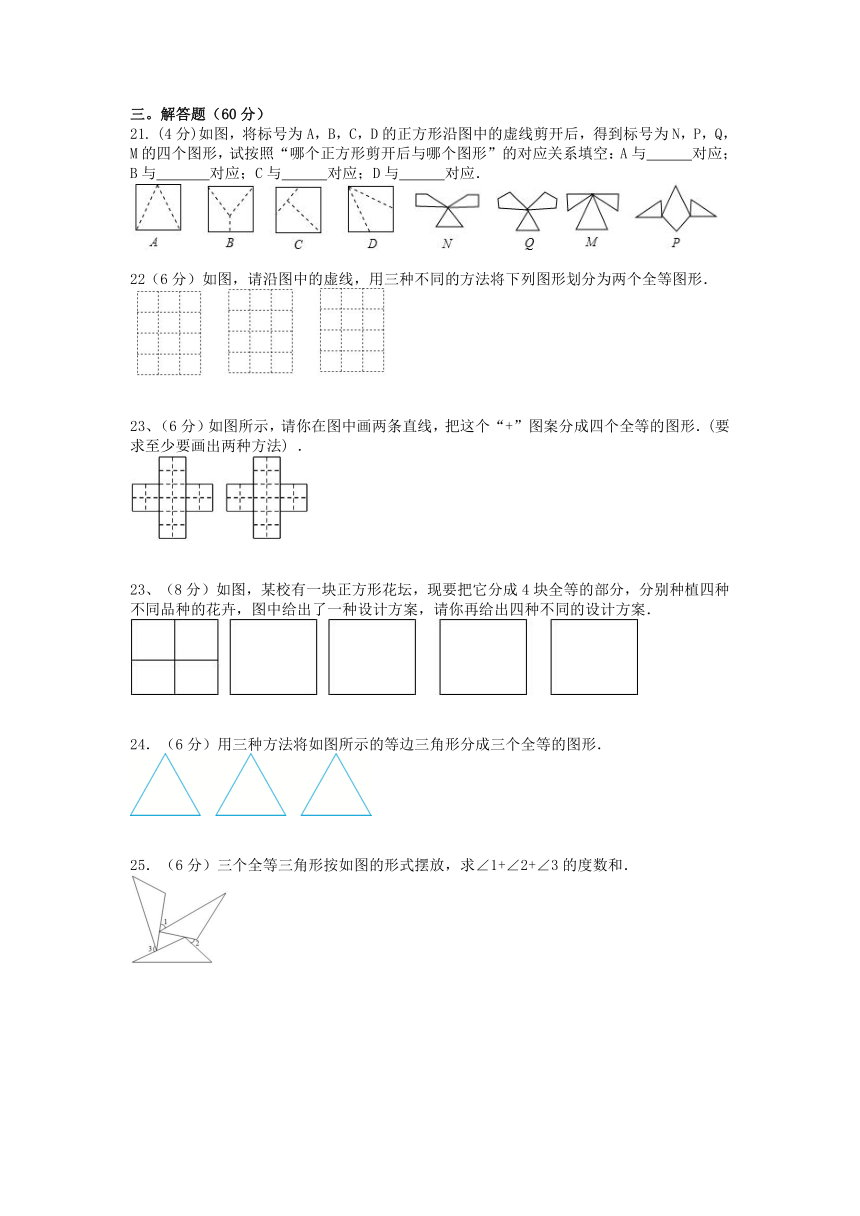
A. B. C. D.
4、小明学习了全等三角形后总结了以下结论:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等、对应角相等;③面积相等的两个三角形是全等图形;④全等三角形的周长相等.其中正确的结论个数是( )
A.1 B.2 C.3 D.4
5、如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
第5题图 第6题图 第7题图
6、在如图所示的图形中,全等图形有( )
A. 1对 B. 2对 C. 3对 D. 4对
7.如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对 B.2对 C.3对 D.4对
8.下列四个图形中,属于全等图形的是( )
A.③和④ B.②和③ C.①和③ D.①②④
第8题图 第9题图
9.如图,A、E、D三点在同一条直线上,且△BAE≌△ACD.若BE=2.5,CD=1,则DE的长为( )
A.1.3 B.1.4 C.1.5 D.无法确定
10.全等三角形又叫做合同三角形.平面内的合同三角形分为真正合同三角形和镜面合同三角形.假如△ABC和△A′B′C′是全等三角形,且点A与点A′对应,点B与点B′对应,点C与点C′对应.当沿周界A﹣B﹣C﹣A及A′﹣B′﹣C′﹣A′环绕时,若运动方向相同,则称它们是真正合同三角形(如图①);若运动方向相反,则称它们是镜面合同三角形(如图②).
两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个翻转180度.下列各组合同三角形中,属于镜面合同三角形的是( )
A. B. C. D.
二.填空题(30分)
11.如图所示的两个三角形全等,则∠α的度数是________.
第11题图 第12题图 第13题图
12.如图,△ABC≌△DEF,则EF的长为__________.
13.如图,在△ABC中,D、E分别是AB、BC上的点.若△ADC≌△EDC≌△EDB,则∠BAC的度数是_______.
14.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2= .
第14题图 第15题图
15.与左图所示图形全等的是 .
16.如图的图案是由全等的图形拼成的其中.AD=0.5 cm,BC=1 cm,则AF= cm.
第16题图 第17题图
17.如图,等边△ABC的边长为1 cm,D,F分别是AB,AC上的点,将△ADE沿直线DE折叠,点A落在点A'处,且点A'在△ABC外部,则阴影部分图形的周长为 cm.
18、如图,在3×3的正方形网格中,∠1+∠2= 度.
第18题图 第19题图 第20题图
19、如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2= 45° .
20、如图,有6幅条形方格图,每个小方格的边长都是1,那么图中由实线围成的图形属于全等图形的是________(填序号).
三。解答题(60分)
21. (4分)如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与 对应;B与 对应;C与 对应;D与 对应.
22(6分)如图,请沿图中的虚线,用三种不同的方法将下列图形划分为两个全等图形.
23、(6分)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(要求至少要画出两种方法) .
23、(8分)如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
24.(6分)用三种方法将如图所示的等边三角形分成三个全等的图形.
25.(6分)三个全等三角形按如图的形式摆放,求∠1+∠2+∠3的度数和.
26.(8分)如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
.
27.(8分)如图锐角△ABC中,F、G分别是AB、AC边上的点,△ACF≌△ADF,△ABG≌△AEG,且DF∥BC∥GE,BG、CF交于点H,若∠BAC=40°求∠BHC的大小。
28. (8分)如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少要多长?(接缝不计).
教师样卷
一.选择题(30分)
1. 两个三角形全等是指这两个三角形的 ( )
A. 形状、大小和位置都相同 B. 形状、大小都相同,与位置没有关系
C. 形状相同,与大小和位置没有关系 D. 形状、大小和位置都没有关系
【答案】B
2、下列各选项中的两个图形属于全等形的是 ( )
【答案】A【解析】解:A.两个图形能够完全重合,故本选项符合题意;
B.圆内两条相交的线段所成的夹角不同,不能完全重合,故本选项不符合题意;
C.两个正方形的边长不相等,不能完全重合,故本选项不符合题意;
D.两个图形中的嘴巴不能完全重合,故本选项不符合题意.
故答案为:A.
3、下列图形中与已知图形全等的是( )
A. B. C. D.
【答案】B【详解】A、圆里面的正方形与已知图形不能重合,错;B、与已知图形能完全重合,正确;C、中间是长方形,与已知图形不重合,错;D、中间是长方形,与已知图形不重合,错.故选:B.
4、小明学习了全等三角形后总结了以下结论:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等、对应角相等;③面积相等的两个三角形是全等图形;④全等三角形的周长相等.其中正确的结论个数是( )
A.1 B.2 C.3 D.4
【答案】C【解析】①全等三角形的形状相同、大小相等,正确;②全等三角形的对应边相等、对应角相等,正确;③面积相等的两个三角形是全等图形,错误;④全等三角形的周长相等,正确.故选:C.
5、如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
【答案】D【解答】解:观察图形可知,∠1所在的三角形与∠3所在的三角形全等,
∴∠1+∠3=90°,又∠2=45°,∴∠1+∠2+∠3=135°,故选:D.
第5题图 第6题图 第7题图
6、在如图所示的图形中,全等图形有( )
A. 1对 B. 2对 C. 3对 D. 4对
【答案】 C 【解析】根据能够完全重合的两个图形是全等形即可判断。
7.如图,△ABC≌△DEF,则此图中相等的线段有( ) [
A.1对 B.2对 C.3对 D.4对
【答案】D
8.下列四个图形中,属于全等图形的是( )
A.③和④ B.②和③ C.①和③ D.①②④
【答案】D
第8题图 第9题图
9.如图,A、E、D三点在同一条直线上,且△BAE≌△ACD.若BE=2.5,CD=1,则DE的长为( )
A.1.3 B.1.4 C.1.5 D.无法确定
【答案】C
10.全等三角形又叫做合同三角形.平面内的合同三角形分为真正合同三角形和镜面合同三角形.假如△ABC和△A′B′C′是全等三角形,且点A与点A′对应,点B与点B′对应,点C与点C′对应.当沿周界A﹣B﹣C﹣A及A′﹣B′﹣C′﹣A′环绕时,若运动方向相同,则称它们是真正合同三角形(如图①);若运动方向相反,则称它们是镜面合同三角形(如图②).
两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个翻转180度.下列各组合同三角形中,属于镜面合同三角形的是( )
A. B. C. D.
【答案】C
二.填空题(30分)
11.如图所示的两个三角形全等,则∠α的度数是____50o_____.
第11题图 第12题图 第13题图
12.如图,△ABC≌△DEF,则EF的长为_____5_____.
13.如图,在△ABC中,D、E分别是AB、BC上的点.若△ADC≌△EDC≌△EDB,则∠BAC的度数是___90o_____.
14.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2= 45o .
第14题图 第15题图
15.与左图所示图形全等的是 (1)(2)(4) .
16.如图的图案是由全等的图形拼成的其中.AD=0.5 cm,BC=1 cm,则AF= 6 cm.
第16题图 第17题图
17.如图,等边△ABC的边长为1 cm,D,F分别是AB,AC上的点,将△ADE沿直线DE折叠,点A落在点A'处,且点A'在△ABC外部,则阴影部分图形的周长为 3 cm.
18、如图,在3×3的正方形网格中,∠1+∠2= 90 度.
第18题图 第19题图 第20题图
19、如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2= 45° .
20、如图,有6幅条形方格图,每个小方格的边长都是1,那么图中由实线围成的图形属于全等图形的是____①⑥、②③⑤____(填序号).
三。解答题(60分)
21. (4分)如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与 M 对应;B与 N 对应;C与 Q 对应;D与 P 对应.
22(6分)如图,请沿图中的虚线,用三种不同的方法将下列图形划分为两个全等图形.
解:如图所示.
23、(6分)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(要求至少要画出两种方法) .
解:如图所示:
23、(8分)如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
【解答】解:设计方案如下:
24.(6分)用三种方法将如图所示的等边三角形分成三个全等的图形.
【解】 如解图所示(答案不唯一)
25.(6分)三个全等三角形按如图的形式摆放,求∠1+∠2+∠3的度数和.
解:如图所示:由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,∵三个
角形全等,∴∠4+∠9+∠6=180°,又∵∠5+∠7+∠8=180°,∴∠1+∠2+∠3+180°+180
=540°,∴∠1+∠2+∠3的度数是180°.
26.(8分)如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
【解】 ∵△ABC≌△ADE,∴∠BAC=∠DAE.∵∠EAB=∠BAC+∠DAC+∠DAE,∠DAC=10°,∠EAB=120°,∴∠BAC=∠DAE=55°.∴∠BAD=∠CAD+∠BAC=65°.
∵∠DFB是△ABF的一个外角,∴∠DFB=∠BAF+∠B=65°+25°=90°.又∵∠DFB是△DFG的一个外角,∴∠DFB=∠D+∠DGB,∴∠DGB=∠DFB-∠D=90°-25°=65°.
27.(8分)如图锐角△ABC中,F、G分别是AB、AC边上的点,△ACF≌△ADF,△ABG≌△AEG,且DF∥BC∥GE,BG、CF交于点H,若∠BAC=40°求∠BHC的大小。
解:延长EG交AB于Q,交AD于P,∵△ACF≌△ADF,△ABG≌△AEG,∠BAC=40°,∴∠DAF=∠BAC=40°,∠EAG=∠BAC=40°,∠D=∠ACF,∠E=∠ABG,∴∠PAE=120°,∴∠APE+∠E=60°,∵DF∥EP,∴∠APE=∠D,∴∠APE=∠ACF,∴∠ABG+∠ACF=60°,∵∠BFH=∠BAC+∠ACF,∴∠BHC=∠ABG+∠BFH=∠ABG+∠BAC+∠ACF=60°+40°=100°,
28. (8分)如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少要多长?(接缝不计).
解:∵后面画出的图形与第一个图形完全一样∴画第二个图形的时候,需往右用1个格,画第三个图的时候,需要再往右用三个格,画第四个图的时候,需要再往右走1个格…
∴画第10个图时,网格的长为4+(1+3+1+3+1+3+1+3+1)=21(cm).
答:这个网格的长至少要21长。
(时间:90分钟 满分:120分)
一.选择题(30分)
1. 两个三角形全等是指这两个三角形的 ( )
A. 形状、大小和位置都相同 B. 形状、大小都相同,与位置没有关系
C. 形状相同,与大小和位置没有关系 D. 形状、大小和位置都没有关系
2、下列各选项中的两个图形属于全等形的是 ( )
3、下列图形中与已知图形全等的是( )
A. B. C. D.
4、小明学习了全等三角形后总结了以下结论:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等、对应角相等;③面积相等的两个三角形是全等图形;④全等三角形的周长相等.其中正确的结论个数是( )
A.1 B.2 C.3 D.4
5、如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
第5题图 第6题图 第7题图
6、在如图所示的图形中,全等图形有( )
A. 1对 B. 2对 C. 3对 D. 4对
7.如图,△ABC≌△DEF,则此图中相等的线段有( )
A.1对 B.2对 C.3对 D.4对
8.下列四个图形中,属于全等图形的是( )
A.③和④ B.②和③ C.①和③ D.①②④
第8题图 第9题图
9.如图,A、E、D三点在同一条直线上,且△BAE≌△ACD.若BE=2.5,CD=1,则DE的长为( )
A.1.3 B.1.4 C.1.5 D.无法确定
10.全等三角形又叫做合同三角形.平面内的合同三角形分为真正合同三角形和镜面合同三角形.假如△ABC和△A′B′C′是全等三角形,且点A与点A′对应,点B与点B′对应,点C与点C′对应.当沿周界A﹣B﹣C﹣A及A′﹣B′﹣C′﹣A′环绕时,若运动方向相同,则称它们是真正合同三角形(如图①);若运动方向相反,则称它们是镜面合同三角形(如图②).
两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个翻转180度.下列各组合同三角形中,属于镜面合同三角形的是( )
A. B. C. D.
二.填空题(30分)
11.如图所示的两个三角形全等,则∠α的度数是________.
第11题图 第12题图 第13题图
12.如图,△ABC≌△DEF,则EF的长为__________.
13.如图,在△ABC中,D、E分别是AB、BC上的点.若△ADC≌△EDC≌△EDB,则∠BAC的度数是_______.
14.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2= .
第14题图 第15题图
15.与左图所示图形全等的是 .
16.如图的图案是由全等的图形拼成的其中.AD=0.5 cm,BC=1 cm,则AF= cm.
第16题图 第17题图
17.如图,等边△ABC的边长为1 cm,D,F分别是AB,AC上的点,将△ADE沿直线DE折叠,点A落在点A'处,且点A'在△ABC外部,则阴影部分图形的周长为 cm.
18、如图,在3×3的正方形网格中,∠1+∠2= 度.
第18题图 第19题图 第20题图
19、如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2= 45° .
20、如图,有6幅条形方格图,每个小方格的边长都是1,那么图中由实线围成的图形属于全等图形的是________(填序号).
三。解答题(60分)
21. (4分)如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与 对应;B与 对应;C与 对应;D与 对应.
22(6分)如图,请沿图中的虚线,用三种不同的方法将下列图形划分为两个全等图形.
23、(6分)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(要求至少要画出两种方法) .
23、(8分)如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
24.(6分)用三种方法将如图所示的等边三角形分成三个全等的图形.
25.(6分)三个全等三角形按如图的形式摆放,求∠1+∠2+∠3的度数和.
26.(8分)如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
.
27.(8分)如图锐角△ABC中,F、G分别是AB、AC边上的点,△ACF≌△ADF,△ABG≌△AEG,且DF∥BC∥GE,BG、CF交于点H,若∠BAC=40°求∠BHC的大小。
28. (8分)如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少要多长?(接缝不计).
教师样卷
一.选择题(30分)
1. 两个三角形全等是指这两个三角形的 ( )
A. 形状、大小和位置都相同 B. 形状、大小都相同,与位置没有关系
C. 形状相同,与大小和位置没有关系 D. 形状、大小和位置都没有关系
【答案】B
2、下列各选项中的两个图形属于全等形的是 ( )
【答案】A【解析】解:A.两个图形能够完全重合,故本选项符合题意;
B.圆内两条相交的线段所成的夹角不同,不能完全重合,故本选项不符合题意;
C.两个正方形的边长不相等,不能完全重合,故本选项不符合题意;
D.两个图形中的嘴巴不能完全重合,故本选项不符合题意.
故答案为:A.
3、下列图形中与已知图形全等的是( )
A. B. C. D.
【答案】B【详解】A、圆里面的正方形与已知图形不能重合,错;B、与已知图形能完全重合,正确;C、中间是长方形,与已知图形不重合,错;D、中间是长方形,与已知图形不重合,错.故选:B.
4、小明学习了全等三角形后总结了以下结论:①全等三角形的形状相同、大小相等;②全等三角形的对应边相等、对应角相等;③面积相等的两个三角形是全等图形;④全等三角形的周长相等.其中正确的结论个数是( )
A.1 B.2 C.3 D.4
【答案】C【解析】①全等三角形的形状相同、大小相等,正确;②全等三角形的对应边相等、对应角相等,正确;③面积相等的两个三角形是全等图形,错误;④全等三角形的周长相等,正确.故选:C.
5、如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
【答案】D【解答】解:观察图形可知,∠1所在的三角形与∠3所在的三角形全等,
∴∠1+∠3=90°,又∠2=45°,∴∠1+∠2+∠3=135°,故选:D.
第5题图 第6题图 第7题图
6、在如图所示的图形中,全等图形有( )
A. 1对 B. 2对 C. 3对 D. 4对
【答案】 C 【解析】根据能够完全重合的两个图形是全等形即可判断。
7.如图,△ABC≌△DEF,则此图中相等的线段有( ) [
A.1对 B.2对 C.3对 D.4对
【答案】D
8.下列四个图形中,属于全等图形的是( )
A.③和④ B.②和③ C.①和③ D.①②④
【答案】D
第8题图 第9题图
9.如图,A、E、D三点在同一条直线上,且△BAE≌△ACD.若BE=2.5,CD=1,则DE的长为( )
A.1.3 B.1.4 C.1.5 D.无法确定
【答案】C
10.全等三角形又叫做合同三角形.平面内的合同三角形分为真正合同三角形和镜面合同三角形.假如△ABC和△A′B′C′是全等三角形,且点A与点A′对应,点B与点B′对应,点C与点C′对应.当沿周界A﹣B﹣C﹣A及A′﹣B′﹣C′﹣A′环绕时,若运动方向相同,则称它们是真正合同三角形(如图①);若运动方向相反,则称它们是镜面合同三角形(如图②).
两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中的一个翻转180度.下列各组合同三角形中,属于镜面合同三角形的是( )
A. B. C. D.
【答案】C
二.填空题(30分)
11.如图所示的两个三角形全等,则∠α的度数是____50o_____.
第11题图 第12题图 第13题图
12.如图,△ABC≌△DEF,则EF的长为_____5_____.
13.如图,在△ABC中,D、E分别是AB、BC上的点.若△ADC≌△EDC≌△EDB,则∠BAC的度数是___90o_____.
14.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2= 45o .
第14题图 第15题图
15.与左图所示图形全等的是 (1)(2)(4) .
16.如图的图案是由全等的图形拼成的其中.AD=0.5 cm,BC=1 cm,则AF= 6 cm.
第16题图 第17题图
17.如图,等边△ABC的边长为1 cm,D,F分别是AB,AC上的点,将△ADE沿直线DE折叠,点A落在点A'处,且点A'在△ABC外部,则阴影部分图形的周长为 3 cm.
18、如图,在3×3的正方形网格中,∠1+∠2= 90 度.
第18题图 第19题图 第20题图
19、如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2= 45° .
20、如图,有6幅条形方格图,每个小方格的边长都是1,那么图中由实线围成的图形属于全等图形的是____①⑥、②③⑤____(填序号).
三。解答题(60分)
21. (4分)如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后,得到标号为N,P,Q,M的四个图形,试按照“哪个正方形剪开后与哪个图形”的对应关系填空:A与 M 对应;B与 N 对应;C与 Q 对应;D与 P 对应.
22(6分)如图,请沿图中的虚线,用三种不同的方法将下列图形划分为两个全等图形.
解:如图所示.
23、(6分)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形.(要求至少要画出两种方法) .
解:如图所示:
23、(8分)如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
【解答】解:设计方案如下:
24.(6分)用三种方法将如图所示的等边三角形分成三个全等的图形.
【解】 如解图所示(答案不唯一)
25.(6分)三个全等三角形按如图的形式摆放,求∠1+∠2+∠3的度数和.
解:如图所示:由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,∵三个
角形全等,∴∠4+∠9+∠6=180°,又∵∠5+∠7+∠8=180°,∴∠1+∠2+∠3+180°+180
=540°,∴∠1+∠2+∠3的度数是180°.
26.(8分)如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
【解】 ∵△ABC≌△ADE,∴∠BAC=∠DAE.∵∠EAB=∠BAC+∠DAC+∠DAE,∠DAC=10°,∠EAB=120°,∴∠BAC=∠DAE=55°.∴∠BAD=∠CAD+∠BAC=65°.
∵∠DFB是△ABF的一个外角,∴∠DFB=∠BAF+∠B=65°+25°=90°.又∵∠DFB是△DFG的一个外角,∴∠DFB=∠D+∠DGB,∴∠DGB=∠DFB-∠D=90°-25°=65°.
27.(8分)如图锐角△ABC中,F、G分别是AB、AC边上的点,△ACF≌△ADF,△ABG≌△AEG,且DF∥BC∥GE,BG、CF交于点H,若∠BAC=40°求∠BHC的大小。
解:延长EG交AB于Q,交AD于P,∵△ACF≌△ADF,△ABG≌△AEG,∠BAC=40°,∴∠DAF=∠BAC=40°,∠EAG=∠BAC=40°,∠D=∠ACF,∠E=∠ABG,∴∠PAE=120°,∴∠APE+∠E=60°,∵DF∥EP,∴∠APE=∠D,∴∠APE=∠ACF,∴∠ABG+∠ACF=60°,∵∠BFH=∠BAC+∠ACF,∴∠BHC=∠ABG+∠BFH=∠ABG+∠BAC+∠ACF=60°+40°=100°,
28. (8分)如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少要多长?(接缝不计).
解:∵后面画出的图形与第一个图形完全一样∴画第二个图形的时候,需往右用1个格,画第三个图的时候,需要再往右用三个格,画第四个图的时候,需要再往右走1个格…
∴画第10个图时,网格的长为4+(1+3+1+3+1+3+1+3+1)=21(cm).
答:这个网格的长至少要21长。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
