2022-2023学年人教版八年级数学上册11.2 与三角形有关的角 同步练习 (Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册11.2 与三角形有关的角 同步练习 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 657.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 17:23:21 | ||
图片预览


文档简介
人教版 11.2 与三角形有关的角
一、选择题(共14小题)
1. 在 中,,若 ,则 的度数为
A. B. C. D.
2. 如图,在 中,,则 为
A. B. C. D.
3. 下列说法正确的是
A. 钝角三角形的内角和大于锐角三角形的内角和
B. 一个三角形至少有两个锐角
C. 钝角三角形的三个内角都是钝角
D. 三角形中较小的两个内角的和一定大于第三个内角
4. 是 的平分线, 是 的邻补角的平分线,,,则
A. B. C. D.
5. 下列各组角度的角不能为同一个三角形的内角的是
A. ,, B. ,,
C. ,, D. ,,
6. 下列说法中错误的是
A. 在 中,,则 为直角三角形
B. 在 中,若 ,则 为直角三角形
C. 在 中,若 ,,则 为直角三角形
D. 在 中,若 ,则 为直角三角形
7. 如图,,则
A. B. C. D.
8. 满足下列条件的三角形中,不是直角三角形的是
A. 三内角之比为 B. 三边长的平方之比为
C. 三边长之比为 D. 三内角之比为
9. 如果三角形最大内角是 ,那么这个三角形是
A. 等腰三角形 B. 等边三角形 C. 不等边三角形 D. 无法确定
10. 如图,已知 ,,,则 等于
A. B. C. D.
11. 中,,, 的对边分别记为 ,,,由下列条件不能判定 为直角三角形的是
A. B.
C. D.
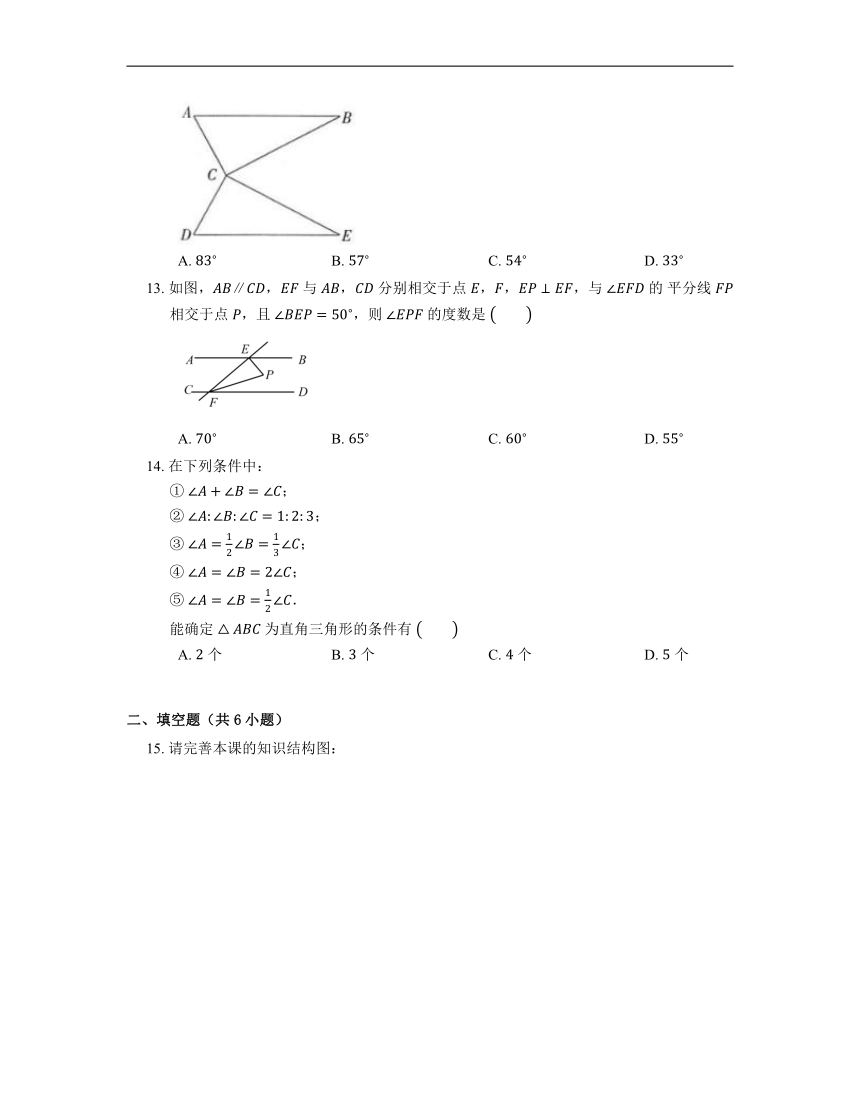
12. 把 与 放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若 ,,则 的度数是
A. B. C. D.
13. 如图,, 与 , 分别相交于点 ,,,与 的 平分线 相交于点 ,且 ,则 的度数是
A. B. C. D.
14. 在下列条件中:
① ;
② ;
③ ;
④ ;
⑤ .
能确定 为直角三角形的条件有
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题)
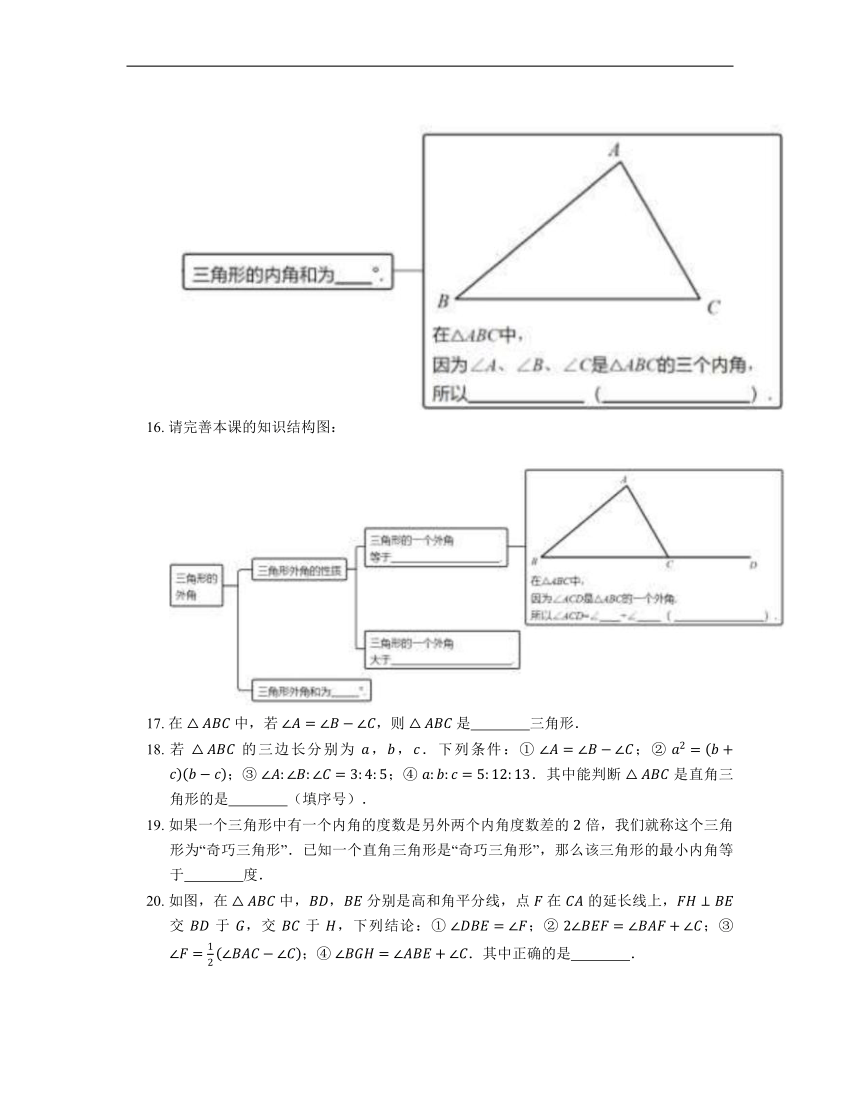
15. 请完善本课的知识结构图:
16. 请完善本课的知识结构图:
17. 在 中,若 ,则 是 三角形.
18. 若 的三边长分别为 ,,.下列条件:① ;② ;③ ;④ .其中能判断 是直角三角形的是 (填序号).
19. 如果一个三角形中有一个内角的度数是另外两个内角度数差的 倍,我们就称这个三角形为“奇巧三角形”.已知一个直角三角形是“奇巧三角形”,那么该三角形的最小内角等于 度.
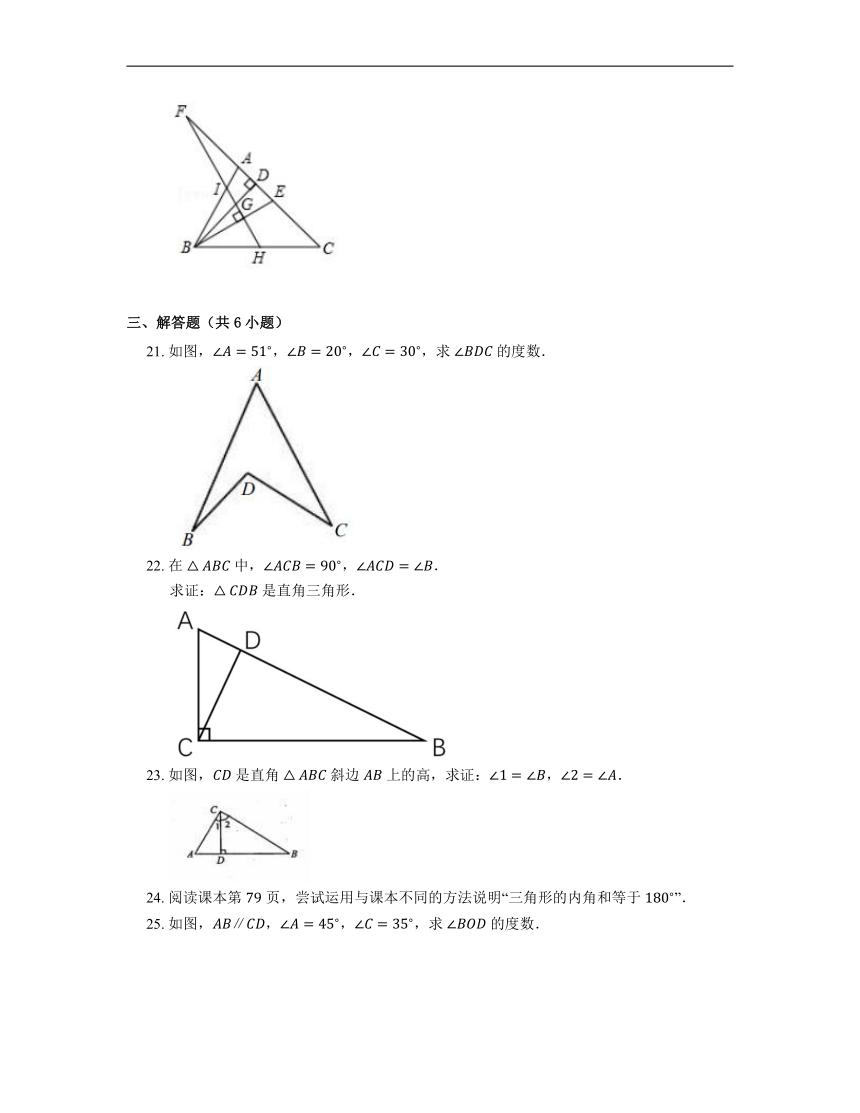
20. 如图,在 中,, 分别是高和角平分线,点 在 的延长线上, 交 于 ,交 于 ,下列结论:① ;② ;③ ;④ .其中正确的是 .
三、解答题(共6小题)
21. 如图,,,,求 的度数.
22. 在 中,,.
求证: 是直角三角形.
23. 如图, 是直角 斜边 上的高,求证:,.
24. 阅读课本第 页,尝试运用与课本不同的方法说明“三角形的内角和等于 ”.
25. 如图,,,,求 的度数.
26. 如图,在 中, 是 的高线, 是 的角平分线,已知 ,.试判断 的形状,并证明你的判断.
答案
1. A
【解析】在 中,,,
则 ,
2. D
【解析】在 中,,则 ,解得 ,
所以 ,即 .
故选D.
3. B
4. A
【解析】 是 的角平分线,,
,
,
是 的角平分线,,
,
故选:A.
5. D
6. D
7. A
【解析】由三角形外角的性质得:,,
,,
,
即:,
,
.
故选:A.
8. D
9. B
10. C
11. B
【解析】A、因为 ,,
所以 ,
所以 为直角三角形,故此选项不合题意;
B、设 ,,,
,
解得:,
则 ,
所以 不是直角三角形,故此选项符合题意;
C、因为 ,
所以 ,
所以 为直角三角形,故此选项不合题意;
D、因为 ,
设 ,,,
因为 ,
所以能构成直角三角形,故此选项不合题意.
12. B
【解析】因为 为直角三角形,且 ,
所以 ,
所以 .
过点 作 ,
所以 ,
又 ,
所以 ,
所以 ,
所以 .
13. A
14. C 【解析】,
若① ,则 ,三角形为直角三角形;
② ,则 ,,,三角形为直角三角形;
③ ,则 ,,,三角形为直角三角形;
④ ,则 ,,三角形不是直角三角形;
⑤ ,则 ,,三角形为等腰直角三角形.
故选C.
15. ,,三角形的内角和为
16. 与它不相邻的两个内角的和,,,三角形的一个外角等于与它不相邻的两个内角的和,任何一个与它不相邻的内角,
17. 直角
18. ①②④
【解析】,
,
,
,
是直角三角形,故①符合题意;
,
,
是直角三角形,故②符合题意;
,,
,,,
不是直角三角形,故③不符合题意;
,
,
是直角三角形,故④符合题意.
19.
【解析】设直角三角形的最小内角为 ,另一个内角为 ,
由题意得,
解得:
答:该三角形的最小内角等于 .
20. ①②③④
【解析】设 交 于点 .
① ,
,
,
,
,
,
①正确;
② 平分 ,
,,
,,
,
②正确;
③ ,
,
,
,
由①得,,
,
;
③正确;
④ ,
,
,
,,
,
,
④正确,
故答案为:①②③④.
21. 如答图,连接 并延长至点 .
在 中,.
在 中,.
,,
.
22. ,
,
,
,
是直角三角形.
23. 略.
24. 如图,过 作 ,
因为 (已知),
所以 (两直线平行,内错角相等),
(两直线平行,同旁内角互补),
所以 ,
即 .
25. .
26. 是直角三角形.
证明:因为 是 的高线,
所以 ,
所以 .
又因为 ,
所以 ,
又因为 ,
所以 .
因为 是 的角平分线,
所以 ,
所以 ,
所以 是直角三角形.
一、选择题(共14小题)
1. 在 中,,若 ,则 的度数为
A. B. C. D.
2. 如图,在 中,,则 为
A. B. C. D.
3. 下列说法正确的是
A. 钝角三角形的内角和大于锐角三角形的内角和
B. 一个三角形至少有两个锐角
C. 钝角三角形的三个内角都是钝角
D. 三角形中较小的两个内角的和一定大于第三个内角
4. 是 的平分线, 是 的邻补角的平分线,,,则
A. B. C. D.
5. 下列各组角度的角不能为同一个三角形的内角的是
A. ,, B. ,,
C. ,, D. ,,
6. 下列说法中错误的是
A. 在 中,,则 为直角三角形
B. 在 中,若 ,则 为直角三角形
C. 在 中,若 ,,则 为直角三角形
D. 在 中,若 ,则 为直角三角形
7. 如图,,则
A. B. C. D.
8. 满足下列条件的三角形中,不是直角三角形的是
A. 三内角之比为 B. 三边长的平方之比为
C. 三边长之比为 D. 三内角之比为
9. 如果三角形最大内角是 ,那么这个三角形是
A. 等腰三角形 B. 等边三角形 C. 不等边三角形 D. 无法确定
10. 如图,已知 ,,,则 等于
A. B. C. D.
11. 中,,, 的对边分别记为 ,,,由下列条件不能判定 为直角三角形的是
A. B.
C. D.
12. 把 与 放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若 ,,则 的度数是
A. B. C. D.
13. 如图,, 与 , 分别相交于点 ,,,与 的 平分线 相交于点 ,且 ,则 的度数是
A. B. C. D.
14. 在下列条件中:
① ;
② ;
③ ;
④ ;
⑤ .
能确定 为直角三角形的条件有
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题)
15. 请完善本课的知识结构图:
16. 请完善本课的知识结构图:
17. 在 中,若 ,则 是 三角形.
18. 若 的三边长分别为 ,,.下列条件:① ;② ;③ ;④ .其中能判断 是直角三角形的是 (填序号).
19. 如果一个三角形中有一个内角的度数是另外两个内角度数差的 倍,我们就称这个三角形为“奇巧三角形”.已知一个直角三角形是“奇巧三角形”,那么该三角形的最小内角等于 度.
20. 如图,在 中,, 分别是高和角平分线,点 在 的延长线上, 交 于 ,交 于 ,下列结论:① ;② ;③ ;④ .其中正确的是 .
三、解答题(共6小题)
21. 如图,,,,求 的度数.
22. 在 中,,.
求证: 是直角三角形.
23. 如图, 是直角 斜边 上的高,求证:,.
24. 阅读课本第 页,尝试运用与课本不同的方法说明“三角形的内角和等于 ”.
25. 如图,,,,求 的度数.
26. 如图,在 中, 是 的高线, 是 的角平分线,已知 ,.试判断 的形状,并证明你的判断.
答案
1. A
【解析】在 中,,,
则 ,
2. D
【解析】在 中,,则 ,解得 ,
所以 ,即 .
故选D.
3. B
4. A
【解析】 是 的角平分线,,
,
,
是 的角平分线,,
,
故选:A.
5. D
6. D
7. A
【解析】由三角形外角的性质得:,,
,,
,
即:,
,
.
故选:A.
8. D
9. B
10. C
11. B
【解析】A、因为 ,,
所以 ,
所以 为直角三角形,故此选项不合题意;
B、设 ,,,
,
解得:,
则 ,
所以 不是直角三角形,故此选项符合题意;
C、因为 ,
所以 ,
所以 为直角三角形,故此选项不合题意;
D、因为 ,
设 ,,,
因为 ,
所以能构成直角三角形,故此选项不合题意.
12. B
【解析】因为 为直角三角形,且 ,
所以 ,
所以 .
过点 作 ,
所以 ,
又 ,
所以 ,
所以 ,
所以 .
13. A
14. C 【解析】,
若① ,则 ,三角形为直角三角形;
② ,则 ,,,三角形为直角三角形;
③ ,则 ,,,三角形为直角三角形;
④ ,则 ,,三角形不是直角三角形;
⑤ ,则 ,,三角形为等腰直角三角形.
故选C.
15. ,,三角形的内角和为
16. 与它不相邻的两个内角的和,,,三角形的一个外角等于与它不相邻的两个内角的和,任何一个与它不相邻的内角,
17. 直角
18. ①②④
【解析】,
,
,
,
是直角三角形,故①符合题意;
,
,
是直角三角形,故②符合题意;
,,
,,,
不是直角三角形,故③不符合题意;
,
,
是直角三角形,故④符合题意.
19.
【解析】设直角三角形的最小内角为 ,另一个内角为 ,
由题意得,
解得:
答:该三角形的最小内角等于 .
20. ①②③④
【解析】设 交 于点 .
① ,
,
,
,
,
,
①正确;
② 平分 ,
,,
,,
,
②正确;
③ ,
,
,
,
由①得,,
,
;
③正确;
④ ,
,
,
,,
,
,
④正确,
故答案为:①②③④.
21. 如答图,连接 并延长至点 .
在 中,.
在 中,.
,,
.
22. ,
,
,
,
是直角三角形.
23. 略.
24. 如图,过 作 ,
因为 (已知),
所以 (两直线平行,内错角相等),
(两直线平行,同旁内角互补),
所以 ,
即 .
25. .
26. 是直角三角形.
证明:因为 是 的高线,
所以 ,
所以 .
又因为 ,
所以 ,
又因为 ,
所以 .
因为 是 的角平分线,
所以 ,
所以 ,
所以 是直角三角形.
