2022-2023学年人教版八年级数学上册11.3 多边形及其内角和同步练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册11.3 多边形及其内角和同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 603.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 17:31:30 | ||
图片预览


文档简介
人教版 11.3 多边形及其内角和
一、选择题(共10小题)
1. 下列图形中,是正多边形的为
A. 直角三角形 B. 等腰三角形 C. 长方形 D. 正方形
2. 如果经过 边形的一个顶点的所有对角线可以将 边形分成 个三角形,那么 的值是
A. B. C. D.
3. 【例 】小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,他购买的瓷砖形状不可以是
A. 正三角形 B. 正四边形 C. 正六边形 D. 正八边形
4. 下列说法正确的是
A. 正五边形是中心对称图形 B. 正十边形的每个内角是
C. 正五边形的中心角是 D. 正十边形的每个外角是
5. 如图,在正五边形 中, 平分 , 平分正五边形的外角 ,则
A. B. C. D.
6. 用正三角形和正六边形密铺成平面,共有 种拼法.
A. B. C. D. 无数
7. 下列说法错误的是
A. 多边形的内角和是它所有内角角度的和
B. 多边形的外角和是它所有外角角度的和
C. 边形的内角和为
D. 边形的外角和为
8. 一个多边形的对角线共有 条,那么这个多边形是
A. 四边形 B. 五边形 C. 六边形 D. 七边形
9. 下列角度不是多边形内角和的是
A. B. C. D.
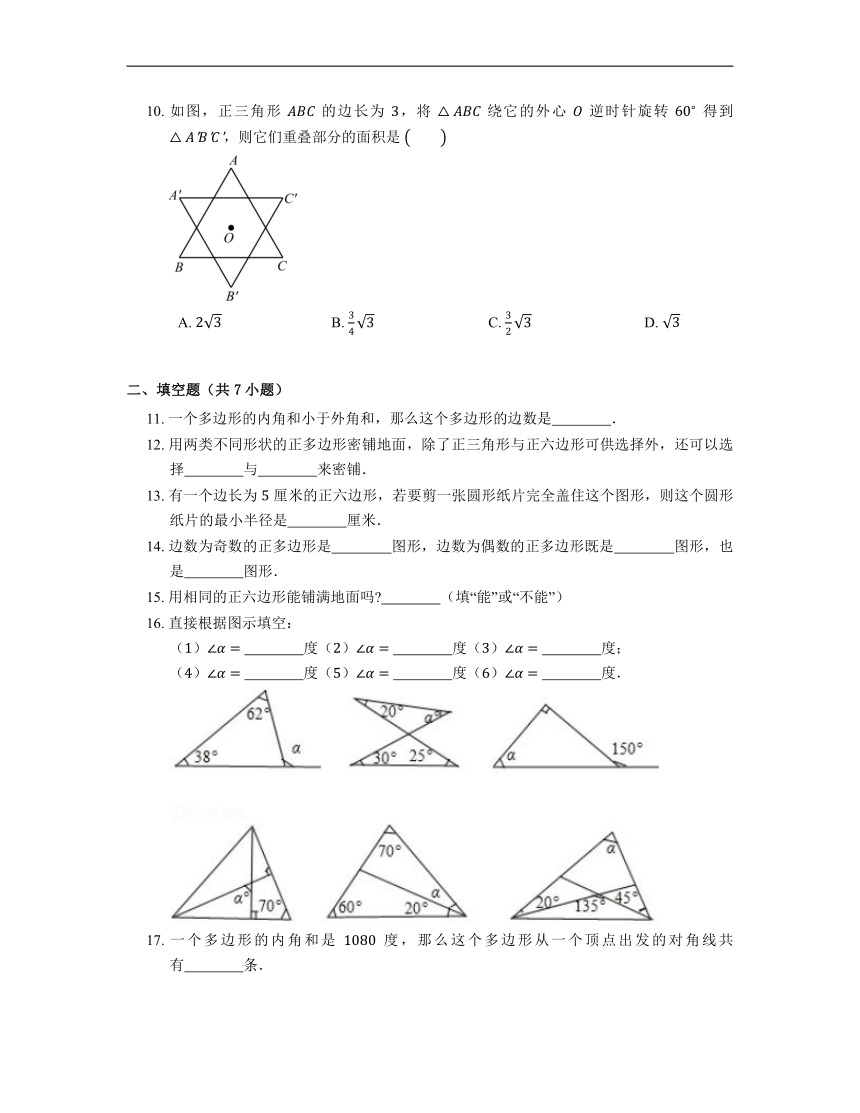
10. 如图,正三角形 的边长为 ,将 绕它的外心 逆时针旋转 得到 ,则它们重叠部分的面积是
A. B. C. D.
二、填空题(共7小题)
11. 一个多边形的内角和小于外角和,那么这个多边形的边数是 .
12. 用两类不同形状的正多边形密铺地面,除了正三角形与正六边形可供选择外,还可以选择 与 来密铺.
13. 有一个边长为 厘米的正六边形,若要剪一张圆形纸片完全盖住这个图形,则这个圆形纸片的最小半径是 厘米.
14. 边数为奇数的正多边形是 图形,边数为偶数的正多边形既是 图形,也是 图形.
15. 用相同的正六边形能铺满地面吗 (填“能”或“不能”)
16. 直接根据图示填空:
() 度() 度() 度;
() 度() 度() 度.
17. 一个多边形的内角和是 度,那么这个多边形从一个顶点出发的对角线共有 条.
三、解答题(共5小题)
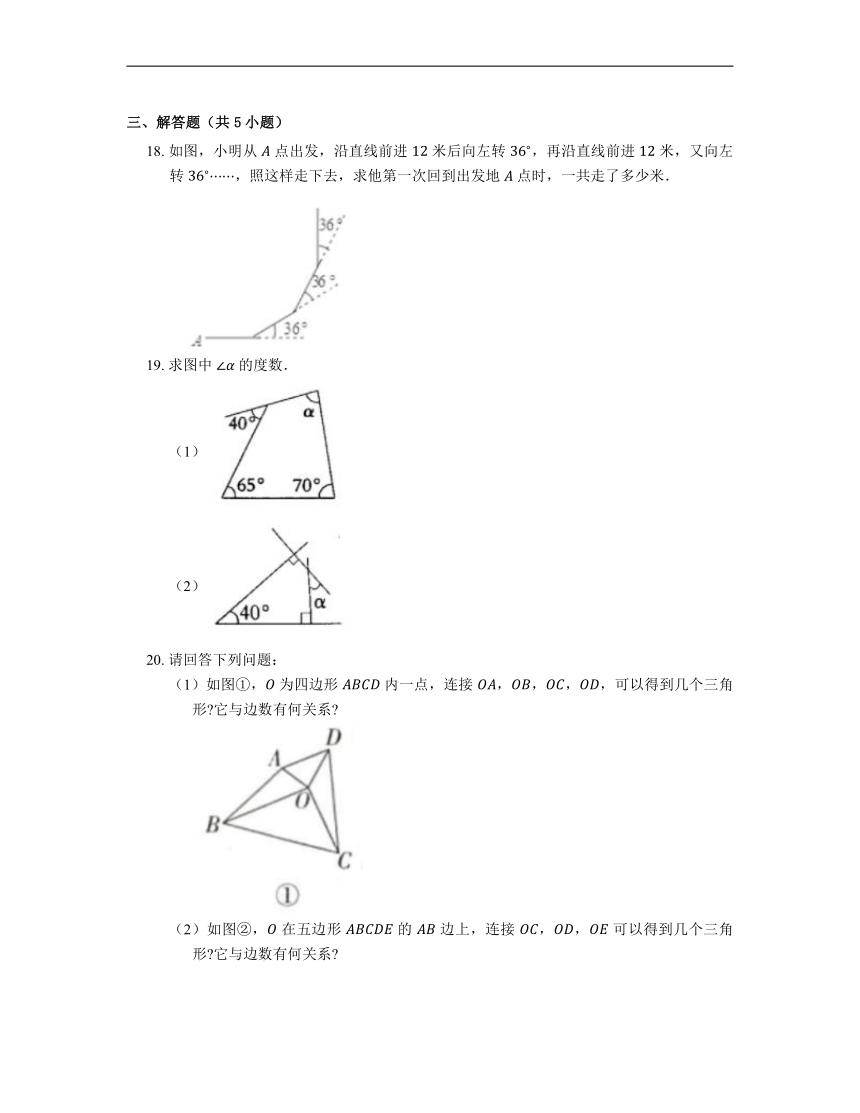
18. 如图,小明从 点出发,沿直线前进 米后向左转 ,再沿直线前进 米,又向左转 ,照这样走下去,求他第一次回到出发地 点时,一共走了多少米.
19. 求图中 的度数.
(1)
(2)
20. 请回答下列问题:
(1)如图①, 为四边形 内一点,连接 ,,,,可以得到几个三角形 它与边数有何关系
(2)如图②, 在五边形 的 边上,连接 ,, 可以得到几个三角形 它与边数有何关系
(3)如图③,过 作六边形 的对角线,可以得到几个三角形 它与边数有何关系
(4)若是任意一个 边形,上述三种情况分别可以将多边形分割成多少个三角形
21. 如果一个多边形的内角和是它的外角和的 倍,那么这个多边形的边数是多少
22. 正三角形、正方形、正六边形(如图 )是我们熟悉的特殊多边形.
(1)这些图形中的边与角有什么共同特征
一般地,我们把各边相等、各内角也相等的多边形叫做正多边形().边数为五的正多边形叫做正五边形(如图 ),边数为六的正多边形叫做正六边形,如图 的两个正多边形分别是正七边形和正八边形.
正多边形有许多优良的性质,匀称美观,常被人们用于图案设计和镶嵌平面(既不留空隙,又不相重叠地拼接)(图 ).
(2)做一做:分别用若干个全等的正三角形、正方形、正六边形纸片,在桌面上设计镶嵌图.你发现这三种正多边形哪些能单独镶嵌平面,哪些不能 你能说明其中的原因吗
(3)想一想:用若干个全等的正五边形能镶嵌平面吗 为什么
事实上,如果用正多边形来镶嵌平面,那么共顶点的各个角之和必须等于 .例如,用正六边形镶嵌平面(图 ),共顶点的 个角之和为 .因此能镶嵌平面的正多边形的内角度数一定能整除 ,所以,能单独镶嵌平面的正多边形只有 种,即正三角形、正方形、正六边形.
如果用多种正多边镶嵌平面,则能镶嵌平面的正多边形就不止上面所说的这 种.
(4)探究:用边长相等的正八边形和正方形能镶嵌平面吗 请说明理由.如果能,画出镶嵌图(只要求画出示意图).
答案
1. D
【解析】正多边形必须同时满足两个条件:
()各边都相等,()各角都相等,只有D选项符合.
2. C
3. D 【解析】因为用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案,
所以小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,他购买的瓷砖形状不可以是正八边形.
故选:D.
4. C
5. B
【解析】由题意得 ,
,
平分 ,
,
平分 ,
,
故选B.
6. B
7. B
8. D
9. C
10. C
【解析】作 于 ,如图:
重合部分是正六边形,连接 和正六边形的各个顶点,所得的三角形都是全等的等边三角形.
是等边三角形,,
,,,
,
的面积 ,
重叠部分的面积 的面积 .
11.
12. 正方形,正八边形(答案不唯一)
13.
14. 轴对称,轴对称,中心对称
15. 能
16. ,,,,,
【解析】();
(),
;
();
()由四边形的内角和为 知: 的邻补角 ;
度;
(),
()由三角形内角和为 知:,
.
故填 ;;;;;.
17.
18. 米.
19. (1) .
(2) .
20. (1) 个三角形,三角形的个数与边数相等.
(2) 个三角形,三角形的个数比边数少 .
(3) 个三角形,三角形的个数比边数少 .
(4) 分别可以分割成 个, 个, 个三角形.
21. 设多边形的边数为 ,则 ,得 .
22. (1) 正三角形、正方形、正六边形的共同特征是各个内角都相等,各条边都相等.
(2) 正三角形、正方形、正六边形都能单独镶嵌平面,因为正三角形的一个内角为 ,将 个正三角形拼在一起,共顶点的 个角之和为 ,刚好拼成一个周角.同理, 个正方形、 个正六边形都能单独拼成周角.
(3) 正五边形不能单独镶嵌平面,因为正五边形的一个内角为 , 个内角和为 , 个内角和为 ,不能拼成周角.
(4) 用边长相等的正八边形和正方形能镶嵌平面.因为正八边形的内角为 ,正方形的内角为 ,由于 ,所以两个正八边形和一个正方形能拼成一幅镶嵌图(如图).
一、选择题(共10小题)
1. 下列图形中,是正多边形的为
A. 直角三角形 B. 等腰三角形 C. 长方形 D. 正方形
2. 如果经过 边形的一个顶点的所有对角线可以将 边形分成 个三角形,那么 的值是
A. B. C. D.
3. 【例 】小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,他购买的瓷砖形状不可以是
A. 正三角形 B. 正四边形 C. 正六边形 D. 正八边形
4. 下列说法正确的是
A. 正五边形是中心对称图形 B. 正十边形的每个内角是
C. 正五边形的中心角是 D. 正十边形的每个外角是
5. 如图,在正五边形 中, 平分 , 平分正五边形的外角 ,则
A. B. C. D.
6. 用正三角形和正六边形密铺成平面,共有 种拼法.
A. B. C. D. 无数
7. 下列说法错误的是
A. 多边形的内角和是它所有内角角度的和
B. 多边形的外角和是它所有外角角度的和
C. 边形的内角和为
D. 边形的外角和为
8. 一个多边形的对角线共有 条,那么这个多边形是
A. 四边形 B. 五边形 C. 六边形 D. 七边形
9. 下列角度不是多边形内角和的是
A. B. C. D.
10. 如图,正三角形 的边长为 ,将 绕它的外心 逆时针旋转 得到 ,则它们重叠部分的面积是
A. B. C. D.
二、填空题(共7小题)
11. 一个多边形的内角和小于外角和,那么这个多边形的边数是 .
12. 用两类不同形状的正多边形密铺地面,除了正三角形与正六边形可供选择外,还可以选择 与 来密铺.
13. 有一个边长为 厘米的正六边形,若要剪一张圆形纸片完全盖住这个图形,则这个圆形纸片的最小半径是 厘米.
14. 边数为奇数的正多边形是 图形,边数为偶数的正多边形既是 图形,也是 图形.
15. 用相同的正六边形能铺满地面吗 (填“能”或“不能”)
16. 直接根据图示填空:
() 度() 度() 度;
() 度() 度() 度.
17. 一个多边形的内角和是 度,那么这个多边形从一个顶点出发的对角线共有 条.
三、解答题(共5小题)
18. 如图,小明从 点出发,沿直线前进 米后向左转 ,再沿直线前进 米,又向左转 ,照这样走下去,求他第一次回到出发地 点时,一共走了多少米.
19. 求图中 的度数.
(1)
(2)
20. 请回答下列问题:
(1)如图①, 为四边形 内一点,连接 ,,,,可以得到几个三角形 它与边数有何关系
(2)如图②, 在五边形 的 边上,连接 ,, 可以得到几个三角形 它与边数有何关系
(3)如图③,过 作六边形 的对角线,可以得到几个三角形 它与边数有何关系
(4)若是任意一个 边形,上述三种情况分别可以将多边形分割成多少个三角形
21. 如果一个多边形的内角和是它的外角和的 倍,那么这个多边形的边数是多少
22. 正三角形、正方形、正六边形(如图 )是我们熟悉的特殊多边形.
(1)这些图形中的边与角有什么共同特征
一般地,我们把各边相等、各内角也相等的多边形叫做正多边形().边数为五的正多边形叫做正五边形(如图 ),边数为六的正多边形叫做正六边形,如图 的两个正多边形分别是正七边形和正八边形.
正多边形有许多优良的性质,匀称美观,常被人们用于图案设计和镶嵌平面(既不留空隙,又不相重叠地拼接)(图 ).
(2)做一做:分别用若干个全等的正三角形、正方形、正六边形纸片,在桌面上设计镶嵌图.你发现这三种正多边形哪些能单独镶嵌平面,哪些不能 你能说明其中的原因吗
(3)想一想:用若干个全等的正五边形能镶嵌平面吗 为什么
事实上,如果用正多边形来镶嵌平面,那么共顶点的各个角之和必须等于 .例如,用正六边形镶嵌平面(图 ),共顶点的 个角之和为 .因此能镶嵌平面的正多边形的内角度数一定能整除 ,所以,能单独镶嵌平面的正多边形只有 种,即正三角形、正方形、正六边形.
如果用多种正多边镶嵌平面,则能镶嵌平面的正多边形就不止上面所说的这 种.
(4)探究:用边长相等的正八边形和正方形能镶嵌平面吗 请说明理由.如果能,画出镶嵌图(只要求画出示意图).
答案
1. D
【解析】正多边形必须同时满足两个条件:
()各边都相等,()各角都相等,只有D选项符合.
2. C
3. D 【解析】因为用一种正多边形镶嵌,只有正三角形,正四边形,正六边形三种正多边形能镶嵌成一个平面图案,
所以小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板,他购买的瓷砖形状不可以是正八边形.
故选:D.
4. C
5. B
【解析】由题意得 ,
,
平分 ,
,
平分 ,
,
故选B.
6. B
7. B
8. D
9. C
10. C
【解析】作 于 ,如图:
重合部分是正六边形,连接 和正六边形的各个顶点,所得的三角形都是全等的等边三角形.
是等边三角形,,
,,,
,
的面积 ,
重叠部分的面积 的面积 .
11.
12. 正方形,正八边形(答案不唯一)
13.
14. 轴对称,轴对称,中心对称
15. 能
16. ,,,,,
【解析】();
(),
;
();
()由四边形的内角和为 知: 的邻补角 ;
度;
(),
()由三角形内角和为 知:,
.
故填 ;;;;;.
17.
18. 米.
19. (1) .
(2) .
20. (1) 个三角形,三角形的个数与边数相等.
(2) 个三角形,三角形的个数比边数少 .
(3) 个三角形,三角形的个数比边数少 .
(4) 分别可以分割成 个, 个, 个三角形.
21. 设多边形的边数为 ,则 ,得 .
22. (1) 正三角形、正方形、正六边形的共同特征是各个内角都相等,各条边都相等.
(2) 正三角形、正方形、正六边形都能单独镶嵌平面,因为正三角形的一个内角为 ,将 个正三角形拼在一起,共顶点的 个角之和为 ,刚好拼成一个周角.同理, 个正方形、 个正六边形都能单独拼成周角.
(3) 正五边形不能单独镶嵌平面,因为正五边形的一个内角为 , 个内角和为 , 个内角和为 ,不能拼成周角.
(4) 用边长相等的正八边形和正方形能镶嵌平面.因为正八边形的内角为 ,正方形的内角为 ,由于 ,所以两个正八边形和一个正方形能拼成一幅镶嵌图(如图).
