2022-2023学年人教版八年级数学上册12.2 三角形全等的判定同步练习(Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2 三角形全等的判定同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 885.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 17:36:47 | ||
图片预览


文档简介
人教版 12.2 三角形全等的判定
一、选择题(共11小题)
1. 如图,, 于点 , 于点 , 与 交于点 ,有下列结论:
① ;
② ;
③点 在 的平分线上.
以上结论正确的
A. 只有① B. 只有② C. 只有③ D. 有①和②和③
2. 如图,点 在 的边 上,用尺规作出了 ,作图痕迹中, 是
A. 以点 为圆心, 的长为半径的弧
B. 以点 为圆心, 的长为半径的弧
C. 以点 为圆心, 的长为半径的弧
D. 以点 为圆心, 的长为半径的弧
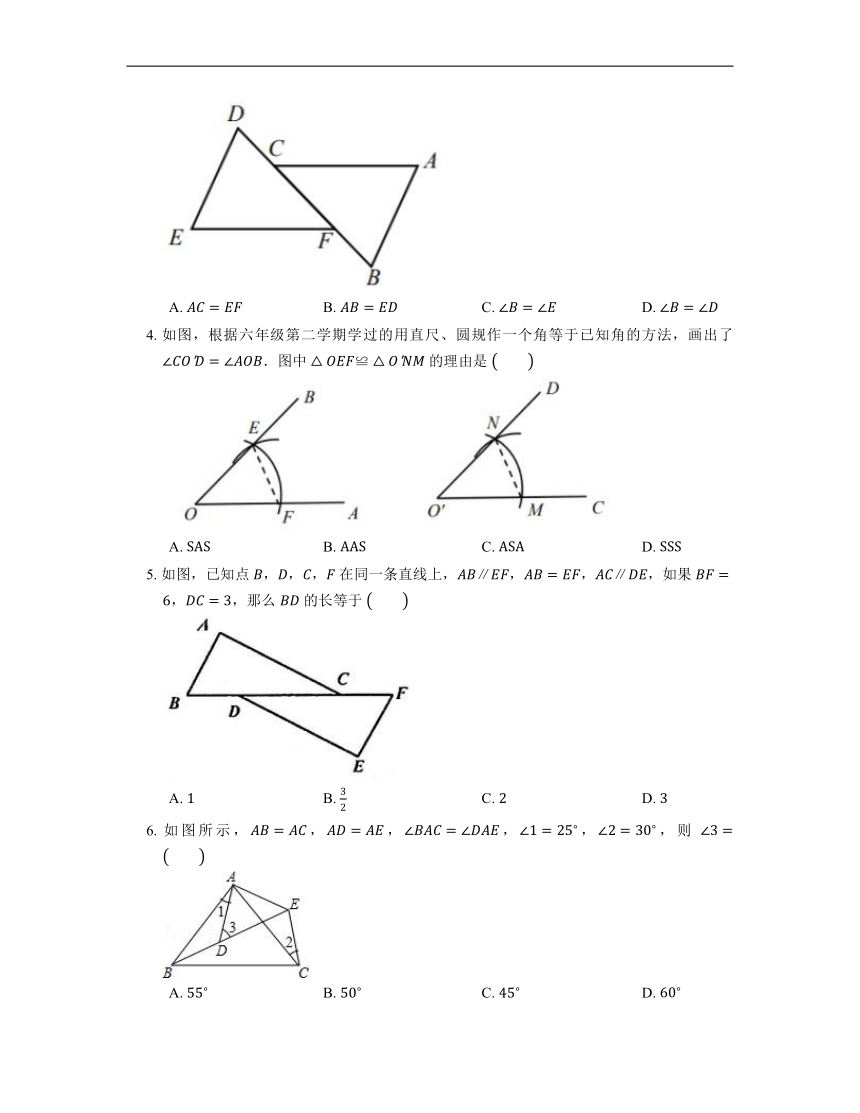
3. 如图,已知 ,,如果要说明 ,那么还可以补充的条件是
A. B. C. D.
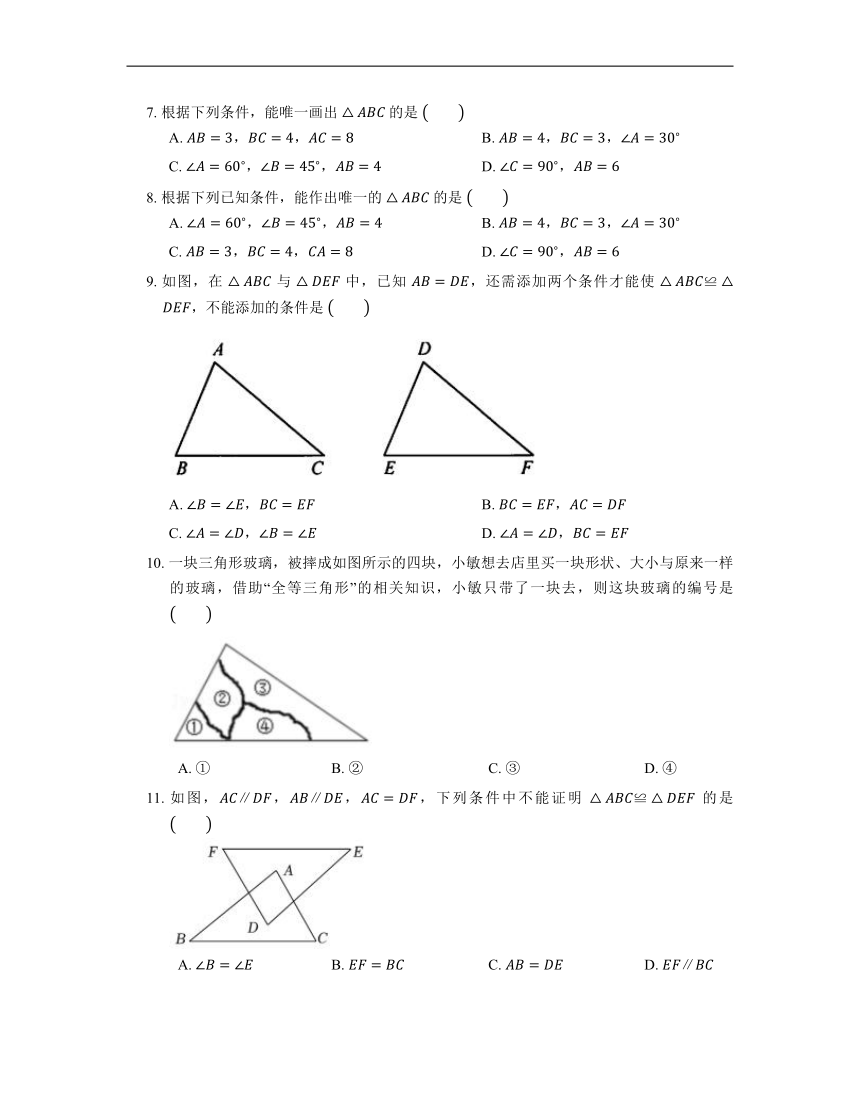
4. 如图,根据六年级第二学期学过的用直尺、圆规作一个角等于已知角的方法,画出了 .图中 的理由是
A. B. C. D.
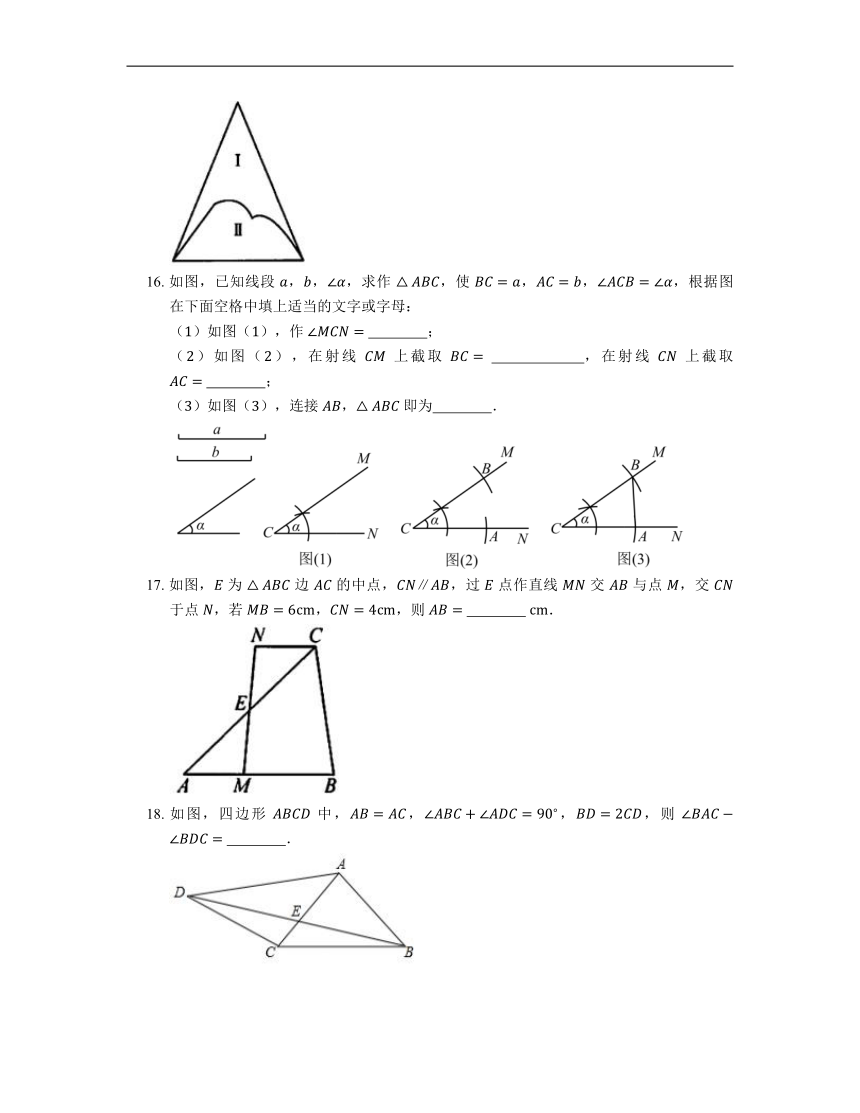
5. 如图,已知点 ,,, 在同一条直线上,,,,如果 ,,那么 的长等于
A. B. C. D.
6. 如图所示,,,,,,则
A. B. C. D.
7. 根据下列条件,能唯一画出 的是
A. ,, B. ,,
C. ,, D. ,
8. 根据下列已知条件,能作出唯一的 的是
A. ,, B. ,,
C. ,, D. ,
9. 如图,在 与 中,已知 ,还需添加两个条件才能使 ,不能添加的条件是
A. , B. ,
C. , D. ,
10. 一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是
A. ① B. ② C. ③ D. ④
11. 如图,,,,下列条件中不能证明 的是
A. B. C. D.
二、填空题(共7小题)
12. 如图,已知 ,, 是 的中点,请填写理由,说明 .
解:因为 ,(已知),
所以 (垂直的意义).
因为 是 的中点(已知),
所以 (线段中点的意义).
在 和 中,
所以 .
13. 用直尺和圆规作一个角等于已知角,如图,能得出 的依据是 .
14. 如图所示,已知 和 均为等边三角形,连接 ,,若 ,则 .
15. 如图,一块三角形玻璃碎成了Ⅰ、Ⅱ两块,现需购买同样大小的一块三角形玻璃,为方便起见,只需带上第 块玻璃碎片.
16. 如图,已知线段 ,,,求作 ,使 ,,,根据图在下面空格中填上适当的文字或字母:
()如图(),作 ;
()如图(),在射线 上截取 ,在射线 上截取 ;
()如图(),连接 , 即为 .
17. 如图, 为 边 的中点,,过 点作直线 交 与点 ,交 于点 ,若 ,,则 .
18. 如图,四边形 中,,,,则 .
三、解答题(共7小题)
19. 请完善本课时的知识结构图.
20. 如图,锐角\triangleABC的两条高BD、CE相交于点O,且CE=BD,若∠ABC=65°,求∠CBD的度数.
21. 如图,已知:线段 ,,其中 .
求作:等腰三角形 ,使底边长 ,腰长 与 的和为 (不要求写作法,但要保留作图痕迹).
22. 请完善本课的知识结构图:
23. 如图,已知 ,,.
(1) 与 全等吗 为什么
(2)如果 , 相交于点 ,连接 ,你还能找出哪几对全等三角形 并直接写出所用的判定方法.
24. 【问题提出】在 中,, 为 的角平分线,探究线段 ,, 的数量关系.
(1)【问题解决】如图 ,当 ,过点 作 ,垂足为 ,易得 ;由此,如图 ,当 时,猜想线段 ,, 有怎样的数量关系 给出证明.
(2)【方法迁移】如图 ,当 , 为 的外角平分线时,探究线段 ,, 又有怎样的数量关系 直接写出结论,不证明.
25. 探究与活动
我们经常看到由全等三角形构成的图案,如图所示的风车、风筝、第 届“国际数学家大会会标”等,请你也利用全等三角形在下列方格中设计一个图案.
答案
1. D
2. C
【解析】由题图可知作图步骤为①以点 为圆心,任意长为半径画弧 ,分别交 , 于 ,;②以点 为圆心,以 的长为半径画弧 ,交 于 ;③以点 为圆心,以 的长为半径画弧 ,交弧 于 ;④过点 作射线 .由上述步骤可知 ,根据同位角相等两直线平行,可得 .
3. B
4. D
5. B
6. A
【解析】,
,
,
在 和 中,
,
,
,
,
故选:A.
7. C
8. A
【解析】当 ,, 时,根据“”可判断 的唯一性.
9. D
10. C
【解析】因为第③块中有完整的两个角以及他们的夹边,利用 易证三角形全等,故应带第 块.
故选:C.
11. B
【解析】延长 交 于 ,
,,
,,
,
A.,,,符合全等三角形的判定定理 ,能推出 ,故本选项不符合题意;
B.,,,不符合全等三角形的判定定理,不能推出 ,故本选项符合题意;
C.,,,符合全等三角形的判定定理 ,能推出 ,故本选项不符合题意;
D.,
,
,
,
,
,, 符合全等三角形的判定定理 ,能推出 ,故本选项不符合题意;
故选:B.
12. ,,,,,,,,,对顶角相等,
13.
【解析】连接 ,,
由作图可得,
,,,
在 和 中,
.
14.
【解析】 和 均为等边三角形,
,,,
,,
,
在 和 中,
,
.
故答案为:.
15. Ⅰ
16. ,,,所求作三角形
17.
18.
【解析】如图,作 ,使 ,
,
,
,
在 和 中,
,
,,
,
,
,
,
,
,
,
,
,
设 ,
,
,
,
,
.
故答案为:.
19.
就是所要画的角.
就是所求作的角.
20. ∵CE⊥AB,BD⊥AC,
∴\triangleBCE和\triangleCBD是直角三角形,
在\mathrm {Rt}\triangleBCE和\mathrm {Rt}\triangleCBD中,
,
∴\mathrm {Rt}\triangleBCE≌\mathrm {Rt}\triangleCBD(HL),
∴∠ABC=∠ACB,
∵∠ABC=65°,
∴∠ACB=65°,
∴∠CBD=90°﹣∠ACB=25°.
【解析】略
21. 如图所示, 即为所求.
22. 判定方法 :在两个三角形中,如果有两边及它们夹角对应相等,那么这两个三角形全等().
判定方法 :在两个三角形中,如果有两角及它们夹边对应相等,那么这两个三角形全等().
判定方法 :在两个三角形中,如果有两角及其中一个角的对边对应相等,那么这两个三角形全等().
判定方法 :在两个三角形中,如果有三边对应相等,那么这两个三角形全等().
23. (1) 全等.
因为 ,(已知),
所以 (垂直的意义).
在 和 中,
所以 .
(2) ;
.
24. (1) 理由:如图,在 上截取 ,连接 ,
为 的平分线,
,
在 和 中,
,
,,
,
,
,
,
,
;
(2) .
【解析】结论:,
理由:如图,在 上截取 ,连接 ,
为 的平分线,
,
在 和 中,
,
,,即 ,
,
,
,
,
,
.
25. 画图略
一、选择题(共11小题)
1. 如图,, 于点 , 于点 , 与 交于点 ,有下列结论:
① ;
② ;
③点 在 的平分线上.
以上结论正确的
A. 只有① B. 只有② C. 只有③ D. 有①和②和③
2. 如图,点 在 的边 上,用尺规作出了 ,作图痕迹中, 是
A. 以点 为圆心, 的长为半径的弧
B. 以点 为圆心, 的长为半径的弧
C. 以点 为圆心, 的长为半径的弧
D. 以点 为圆心, 的长为半径的弧
3. 如图,已知 ,,如果要说明 ,那么还可以补充的条件是
A. B. C. D.
4. 如图,根据六年级第二学期学过的用直尺、圆规作一个角等于已知角的方法,画出了 .图中 的理由是
A. B. C. D.
5. 如图,已知点 ,,, 在同一条直线上,,,,如果 ,,那么 的长等于
A. B. C. D.
6. 如图所示,,,,,,则
A. B. C. D.
7. 根据下列条件,能唯一画出 的是
A. ,, B. ,,
C. ,, D. ,
8. 根据下列已知条件,能作出唯一的 的是
A. ,, B. ,,
C. ,, D. ,
9. 如图,在 与 中,已知 ,还需添加两个条件才能使 ,不能添加的条件是
A. , B. ,
C. , D. ,
10. 一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是
A. ① B. ② C. ③ D. ④
11. 如图,,,,下列条件中不能证明 的是
A. B. C. D.
二、填空题(共7小题)
12. 如图,已知 ,, 是 的中点,请填写理由,说明 .
解:因为 ,(已知),
所以 (垂直的意义).
因为 是 的中点(已知),
所以 (线段中点的意义).
在 和 中,
所以 .
13. 用直尺和圆规作一个角等于已知角,如图,能得出 的依据是 .
14. 如图所示,已知 和 均为等边三角形,连接 ,,若 ,则 .
15. 如图,一块三角形玻璃碎成了Ⅰ、Ⅱ两块,现需购买同样大小的一块三角形玻璃,为方便起见,只需带上第 块玻璃碎片.
16. 如图,已知线段 ,,,求作 ,使 ,,,根据图在下面空格中填上适当的文字或字母:
()如图(),作 ;
()如图(),在射线 上截取 ,在射线 上截取 ;
()如图(),连接 , 即为 .
17. 如图, 为 边 的中点,,过 点作直线 交 与点 ,交 于点 ,若 ,,则 .
18. 如图,四边形 中,,,,则 .
三、解答题(共7小题)
19. 请完善本课时的知识结构图.
20. 如图,锐角\triangleABC的两条高BD、CE相交于点O,且CE=BD,若∠ABC=65°,求∠CBD的度数.
21. 如图,已知:线段 ,,其中 .
求作:等腰三角形 ,使底边长 ,腰长 与 的和为 (不要求写作法,但要保留作图痕迹).
22. 请完善本课的知识结构图:
23. 如图,已知 ,,.
(1) 与 全等吗 为什么
(2)如果 , 相交于点 ,连接 ,你还能找出哪几对全等三角形 并直接写出所用的判定方法.
24. 【问题提出】在 中,, 为 的角平分线,探究线段 ,, 的数量关系.
(1)【问题解决】如图 ,当 ,过点 作 ,垂足为 ,易得 ;由此,如图 ,当 时,猜想线段 ,, 有怎样的数量关系 给出证明.
(2)【方法迁移】如图 ,当 , 为 的外角平分线时,探究线段 ,, 又有怎样的数量关系 直接写出结论,不证明.
25. 探究与活动
我们经常看到由全等三角形构成的图案,如图所示的风车、风筝、第 届“国际数学家大会会标”等,请你也利用全等三角形在下列方格中设计一个图案.
答案
1. D
2. C
【解析】由题图可知作图步骤为①以点 为圆心,任意长为半径画弧 ,分别交 , 于 ,;②以点 为圆心,以 的长为半径画弧 ,交 于 ;③以点 为圆心,以 的长为半径画弧 ,交弧 于 ;④过点 作射线 .由上述步骤可知 ,根据同位角相等两直线平行,可得 .
3. B
4. D
5. B
6. A
【解析】,
,
,
在 和 中,
,
,
,
,
故选:A.
7. C
8. A
【解析】当 ,, 时,根据“”可判断 的唯一性.
9. D
10. C
【解析】因为第③块中有完整的两个角以及他们的夹边,利用 易证三角形全等,故应带第 块.
故选:C.
11. B
【解析】延长 交 于 ,
,,
,,
,
A.,,,符合全等三角形的判定定理 ,能推出 ,故本选项不符合题意;
B.,,,不符合全等三角形的判定定理,不能推出 ,故本选项符合题意;
C.,,,符合全等三角形的判定定理 ,能推出 ,故本选项不符合题意;
D.,
,
,
,
,
,, 符合全等三角形的判定定理 ,能推出 ,故本选项不符合题意;
故选:B.
12. ,,,,,,,,,对顶角相等,
13.
【解析】连接 ,,
由作图可得,
,,,
在 和 中,
.
14.
【解析】 和 均为等边三角形,
,,,
,,
,
在 和 中,
,
.
故答案为:.
15. Ⅰ
16. ,,,所求作三角形
17.
18.
【解析】如图,作 ,使 ,
,
,
,
在 和 中,
,
,,
,
,
,
,
,
,
,
,
,
设 ,
,
,
,
,
.
故答案为:.
19.
就是所要画的角.
就是所求作的角.
20. ∵CE⊥AB,BD⊥AC,
∴\triangleBCE和\triangleCBD是直角三角形,
在\mathrm {Rt}\triangleBCE和\mathrm {Rt}\triangleCBD中,
,
∴\mathrm {Rt}\triangleBCE≌\mathrm {Rt}\triangleCBD(HL),
∴∠ABC=∠ACB,
∵∠ABC=65°,
∴∠ACB=65°,
∴∠CBD=90°﹣∠ACB=25°.
【解析】略
21. 如图所示, 即为所求.
22. 判定方法 :在两个三角形中,如果有两边及它们夹角对应相等,那么这两个三角形全等().
判定方法 :在两个三角形中,如果有两角及它们夹边对应相等,那么这两个三角形全等().
判定方法 :在两个三角形中,如果有两角及其中一个角的对边对应相等,那么这两个三角形全等().
判定方法 :在两个三角形中,如果有三边对应相等,那么这两个三角形全等().
23. (1) 全等.
因为 ,(已知),
所以 (垂直的意义).
在 和 中,
所以 .
(2) ;
.
24. (1) 理由:如图,在 上截取 ,连接 ,
为 的平分线,
,
在 和 中,
,
,,
,
,
,
,
,
;
(2) .
【解析】结论:,
理由:如图,在 上截取 ,连接 ,
为 的平分线,
,
在 和 中,
,
,,即 ,
,
,
,
,
,
.
25. 画图略
