2022-2023学年人教版八年级数学上册 第一学段(11.1—13.1)综合练习题 (Word版,含解析)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 第一学段(11.1—13.1)综合练习题 (Word版,含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 270.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 17:51:51 | ||
图片预览


文档简介
2022-2023学年人教版八年级数学上册第一学段综合练习题(附答案)(范围:11.1—13.1)
一、选择题
1.永州市教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育,下列安全图标不是轴对称的是( )
A.注意安全 B.水深危险
C.必须戴安全帽 D.注意通风
2.一个三角形的两边长分别为3和8,则它的第三边长可能是( )
A.5 B.12 C.10 D.无法确定
3.下列四个图形中,线段BE是△ABC的高的图形是( )
A. B.
C. D.
4.如图,△ABC与△A'B'C'关于直线l对称,则∠B的度数为( )
A.30° B.50° C.90° D.100°
5.下列条件能判定△ABC≌△DEF的一组是( )
A.∠A=∠D,∠B=∠E,∠C=∠F B.AB=DE,BC=EF,∠A=∠D
C.∠A=∠D,∠C=∠F,AC=DF D.△ABC的周长等于△DEF的周长
6.如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,∠A=50°,则∠BOC=( )
A.50° B.65° C.105° D.115°
7.如图,在OA,OB上分别截取OD,OE,使OD=OE,再分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内交于点C,作射线OC,OC就是∠AOB的角平分线.这是因为连结CD,CE,可得到△COD≌△COE,根据全等三角形对应角相等,可得∠COD=∠COE.在这个过程中,得到△COD≌△COE的条件是( )
A.SAS B.AAS C.ASA D.SSS
8.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=2:3:5 B.∠A﹣∠C=∠B
C.∠A=∠B=2∠C D.∠A=∠B=∠C
9.如图,在△ABC中,点D在边BC上,点E,F分别是AD,CE的中点,且△BEF的面积为3,则△ABC的面积是( )
A.9 B.10 C.11 D.12
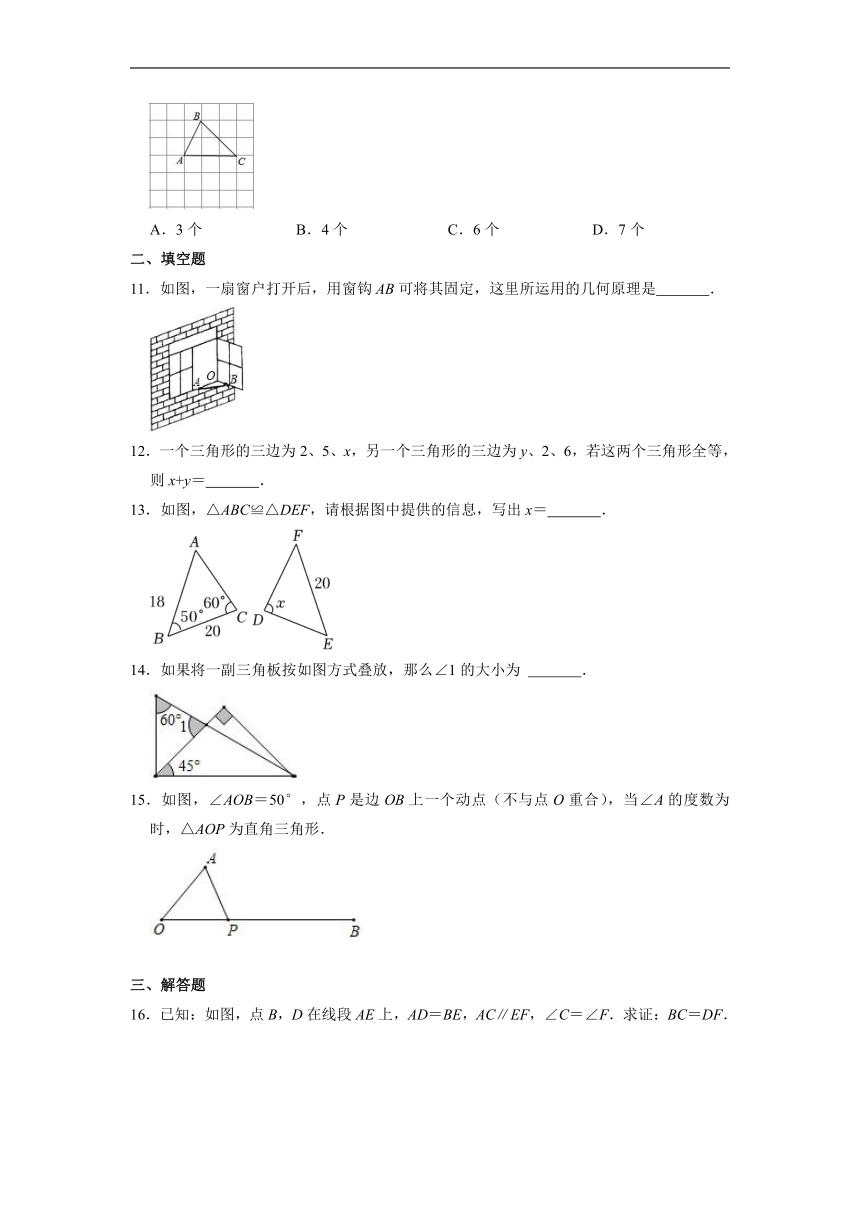
10.在如图所示的6×6网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数是( )
A.3个 B.4个 C.6个 D.7个
二、填空题
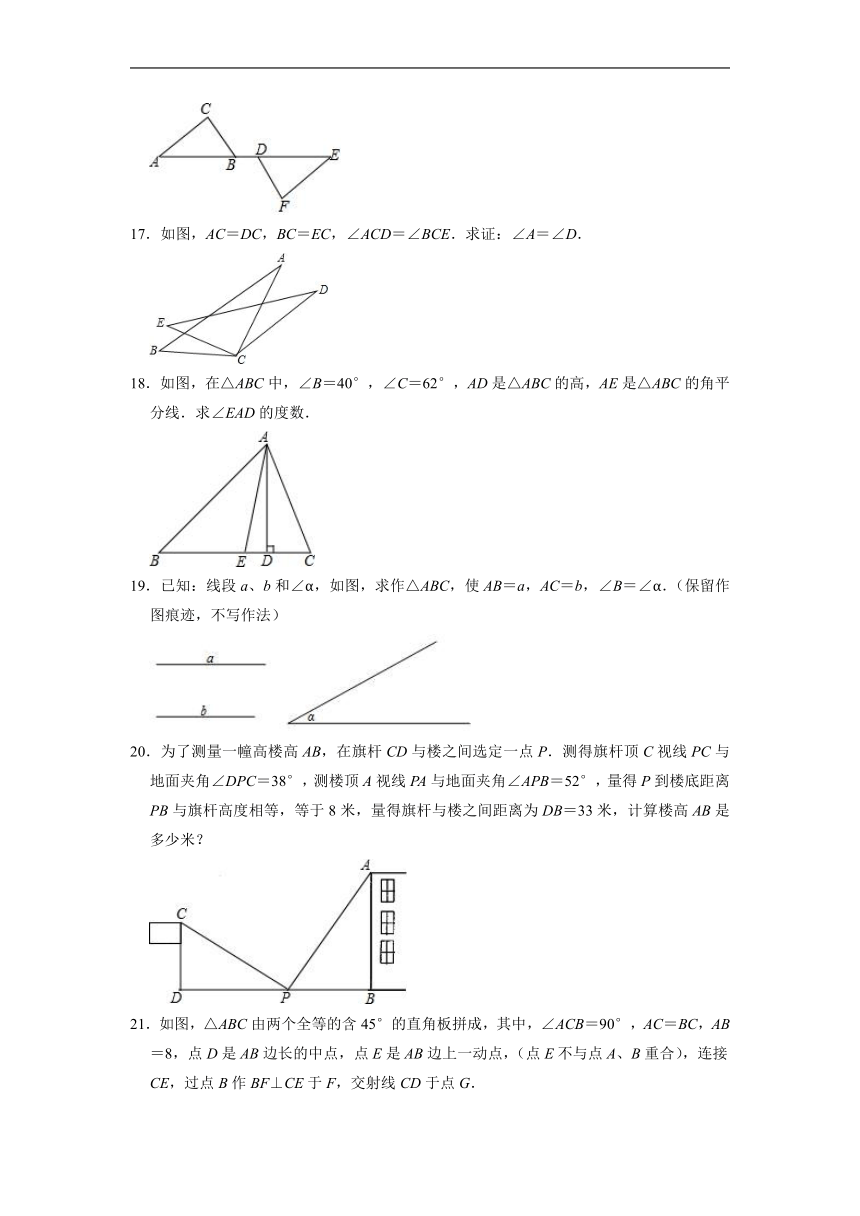
11.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是 .
12.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= .
13.如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .
14.如果将一副三角板按如图方式叠放,那么∠1的大小为 .
15.如图,∠AOB=50°,点P是边OB上一个动点(不与点O重合),当∠A的度数为 时,△AOP为直角三角形.
三、解答题
16.已知:如图,点B,D在线段AE上,AD=BE,AC∥EF,∠C=∠F.求证:BC=DF.
17.如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.
18.如图,在△ABC中,∠B=40°,∠C=62°,AD是△ABC的高,AE是△ABC的角平分线.求∠EAD的度数.
19.已知:线段a、b和∠α,如图,求作△ABC,使AB=a,AC=b,∠B=∠α.(保留作图痕迹,不写作法)
20.为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=38°,测楼顶A视线PA与地面夹角∠APB=52°,量得P到楼底距离PB与旗杆高度相等,等于8米,量得旗杆与楼之间距离为DB=33米,计算楼高AB是多少米?
21.如图,△ABC由两个全等的含45°的直角板拼成,其中,∠ACB=90°,AC=BC,AB=8,点D是AB边长的中点,点E是AB边上一动点,(点E不与点A、B重合),连接CE,过点B作BF⊥CE于F,交射线CD于点G.
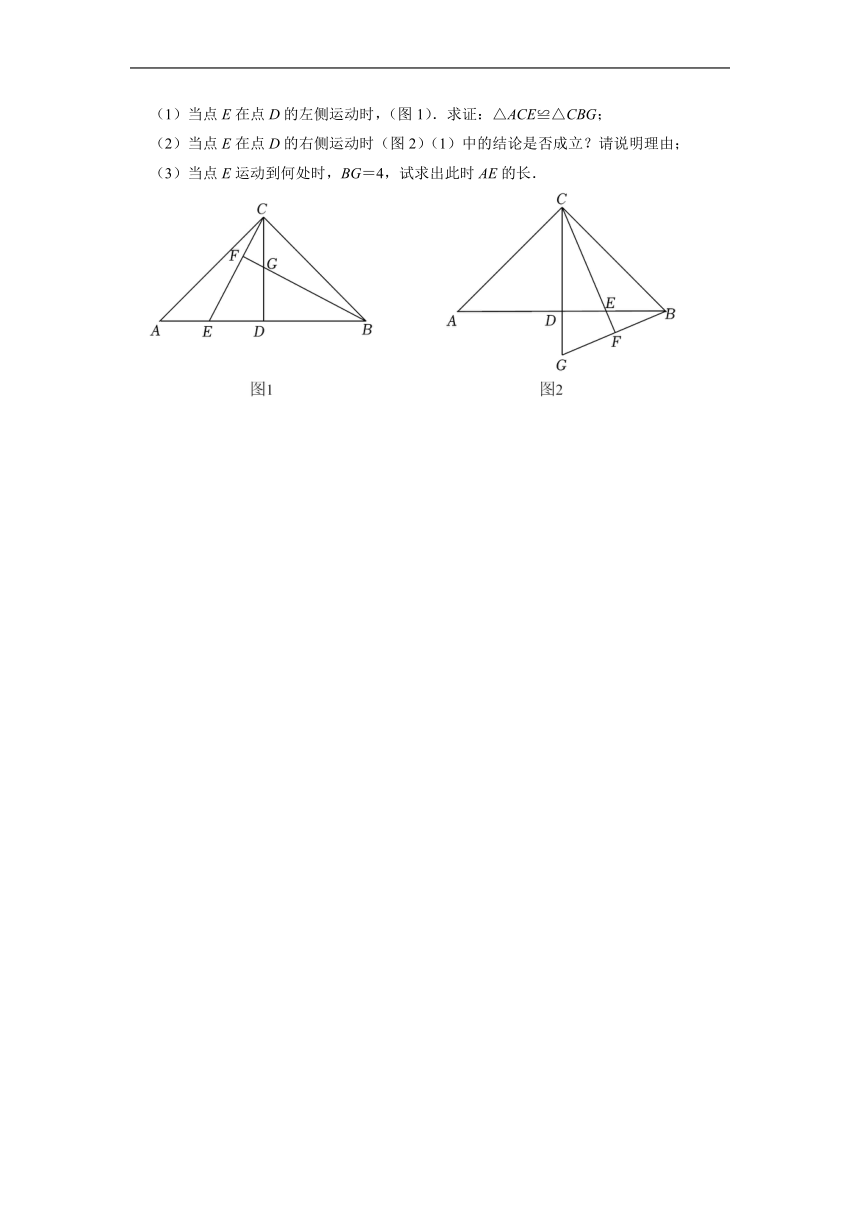
(1)当点E在点D的左侧运动时,(图1).求证:△ACE≌△CBG;
(2)当点E在点D的右侧运动时(图2)(1)中的结论是否成立?请说明理由;
(3)当点E运动到何处时,BG=4,试求出此时AE的长.
参考答案
一、选择题
1.解:A,B,C选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
D选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
故选:D.
2.解:∵此三角形的两边长分别为3和8,
∴第三边长的取值范围是:8﹣3<第三边<8+3.
即5<第三边<11,
观察选项,只有选项C符合题意.
故选:C.
3.解:线段BE是△ABC的高的图是选项A.
故选:A.
4.解:∵△ABC与△A'B'C'关于直线l对称,
∴∠C=∠C′=30°,
∵∠A=60°,
∴∠B=180°﹣∠A﹣∠C=90°.
则∠B的度数为90°.
故选:C.
5.解:A、∠A=∠D,∠B=∠E,∠C=∠F是AAA,不能判定两三角形全等,故选项不符合题意;
B、AB=DE,BC=EF,∠A=∠D是SSA,不能判定两三角形全等,故选项不符合题意;
C、∠A=∠D,∠C=∠F,AC=DF符合ASA,能判定两三角形全等,故选项符合题意;
D、△ABC的周长等于△DEF的周长,三边不可能相等,故选项不符合题意.
故选:C.
6.解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°,
∵BO平分∠ABC,CO平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=65°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣65°=115°.
故选:D.
7.解:由作图可知,OE=OD,EC=DC,
在△OCE和△OCD中,
,
∴△OCE≌△OCD(SSS),
∴∠COD=∠COE.
故选:D.
8.解:A、最大角∠C=×180°=90°,是直角三角形,不符合题意;
B、由∠A﹣∠C=∠B,可得∠A=∠B+∠C,
故最大角∠A=180°÷2=90°,是直角三角形,不符合题意;
C、设∠A=∠B=x,则∠C=x,
所以,x+x+x=180°,
解得x=72°,
最大角∠A=∠B=72°,是锐角三角形,符合题意;
D、设∠A=x,则∠B=2x,∠C=3x,
所以,x+2x+3x=180°,
解得x=30°,
最大角∠C=3×30°=90°,是直角三角形,不符合题意;
故选:C.
9.解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC,
∴S△BCE=S△ABC,
∵点F是CE的中点,
∴S△BEF=S△BCE=S△ABC,
∵△BEF的面积为3,
∴S△ABC=4×3=12.
故选:D.
10.解:如图所示:一共有7个符合题意的点.
故选:D.
二、填空题
11.解:一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是三角形的稳定性.
故答案为:三角形的稳定性.
12.解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5
∴x+y=11.
故答案为:11.
13.解:∵△ABC≌△DEF,
∴BC=20=EF,∠A=∠D=x,
∵∠B=50°,∠C=60°,
∴∠A=180°﹣50°﹣60°=70°,
∴x=70°,
故答案为:70°.
14.解:如图,
由题意得:∠2=30°,∠3=45°,
∴∠1=∠2+∠3=75°.
故答案为:75°.
15.解:若△AOP为直角三角形,则
①∠A=90°时,△AOP为直角三角形;
②当∠APO=90°时,△AOP为直角三角形,此时∠A=40°.
故答案为90°或40°.
三、解答题
16.证明:∵AD=BE,
∴AD﹣BD=BE﹣BD,
∴AB=ED,
∵AC∥EF,
∴∠A=∠E,
在△ABC和△EDF中,,
∴△ABC≌△EDF(AAS),
∴BC=DF.
17.证明:∵∠ACD=∠BCE,
∴∠ACB=∠DCE,
在△BCA和△ECD中,
,
∴△ABC≌△DEC(SAS),
∴∠A=∠D.
18.解:∵∠B=40°,∠C=62°,
∴∠BAC=180°﹣62°﹣40°=78°,
∵AE为∠BAC角平分线,
∴∠BAE=78°÷2=39°,
∵AD为△ABC的高,
∴∠ADB=90°,
∴∠DAC=90°﹣∠C=90°﹣62°=28°,
∴∠EAD=∠EAC﹣∠DAC=39°﹣28°=11°,
即∠EAD的度数是11°.
19.解:如图,△ABC和△ABC′为所作.
20.解:∵∠CPD=38°,∠APB=52°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=52°,
在△CPD和△PAB中
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=33,PB=8,
∴AB=33﹣8=25(m),
答:楼高AB是25米.
21.(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°,
∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△ACE和△CBG中,
,
∴△ACE≌△CBG(ASA);
(2)解:(1)中结论成立,理由如下:
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△ACE和△CBG中,
,
∴△ACE≌△CBG(ASA);
(3)解:在Rt△ABC中,AC=BC,点D是AB的中点,
∴CD⊥AB,CD=AD=BD=AB=4,
∵BG=4,
∴BD=BG,
∴点G、E、F、D四点重合,
∴当点E运动到点D时,BG=4,此时AE的长为4.
一、选择题
1.永州市教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育,下列安全图标不是轴对称的是( )
A.注意安全 B.水深危险
C.必须戴安全帽 D.注意通风
2.一个三角形的两边长分别为3和8,则它的第三边长可能是( )
A.5 B.12 C.10 D.无法确定
3.下列四个图形中,线段BE是△ABC的高的图形是( )
A. B.
C. D.
4.如图,△ABC与△A'B'C'关于直线l对称,则∠B的度数为( )
A.30° B.50° C.90° D.100°
5.下列条件能判定△ABC≌△DEF的一组是( )
A.∠A=∠D,∠B=∠E,∠C=∠F B.AB=DE,BC=EF,∠A=∠D
C.∠A=∠D,∠C=∠F,AC=DF D.△ABC的周长等于△DEF的周长
6.如图,在△ABC中,BO平分∠ABC,CO平分∠ACB,∠A=50°,则∠BOC=( )
A.50° B.65° C.105° D.115°
7.如图,在OA,OB上分别截取OD,OE,使OD=OE,再分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内交于点C,作射线OC,OC就是∠AOB的角平分线.这是因为连结CD,CE,可得到△COD≌△COE,根据全等三角形对应角相等,可得∠COD=∠COE.在这个过程中,得到△COD≌△COE的条件是( )
A.SAS B.AAS C.ASA D.SSS
8.给定下列条件,不能判定三角形是直角三角形的是( )
A.∠A:∠B:∠C=2:3:5 B.∠A﹣∠C=∠B
C.∠A=∠B=2∠C D.∠A=∠B=∠C
9.如图,在△ABC中,点D在边BC上,点E,F分别是AD,CE的中点,且△BEF的面积为3,则△ABC的面积是( )
A.9 B.10 C.11 D.12
10.在如图所示的6×6网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数是( )
A.3个 B.4个 C.6个 D.7个
二、填空题
11.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是 .
12.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= .
13.如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .
14.如果将一副三角板按如图方式叠放,那么∠1的大小为 .
15.如图,∠AOB=50°,点P是边OB上一个动点(不与点O重合),当∠A的度数为 时,△AOP为直角三角形.
三、解答题
16.已知:如图,点B,D在线段AE上,AD=BE,AC∥EF,∠C=∠F.求证:BC=DF.
17.如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.
18.如图,在△ABC中,∠B=40°,∠C=62°,AD是△ABC的高,AE是△ABC的角平分线.求∠EAD的度数.
19.已知:线段a、b和∠α,如图,求作△ABC,使AB=a,AC=b,∠B=∠α.(保留作图痕迹,不写作法)
20.为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=38°,测楼顶A视线PA与地面夹角∠APB=52°,量得P到楼底距离PB与旗杆高度相等,等于8米,量得旗杆与楼之间距离为DB=33米,计算楼高AB是多少米?
21.如图,△ABC由两个全等的含45°的直角板拼成,其中,∠ACB=90°,AC=BC,AB=8,点D是AB边长的中点,点E是AB边上一动点,(点E不与点A、B重合),连接CE,过点B作BF⊥CE于F,交射线CD于点G.
(1)当点E在点D的左侧运动时,(图1).求证:△ACE≌△CBG;
(2)当点E在点D的右侧运动时(图2)(1)中的结论是否成立?请说明理由;
(3)当点E运动到何处时,BG=4,试求出此时AE的长.
参考答案
一、选择题
1.解:A,B,C选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
D选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
故选:D.
2.解:∵此三角形的两边长分别为3和8,
∴第三边长的取值范围是:8﹣3<第三边<8+3.
即5<第三边<11,
观察选项,只有选项C符合题意.
故选:C.
3.解:线段BE是△ABC的高的图是选项A.
故选:A.
4.解:∵△ABC与△A'B'C'关于直线l对称,
∴∠C=∠C′=30°,
∵∠A=60°,
∴∠B=180°﹣∠A﹣∠C=90°.
则∠B的度数为90°.
故选:C.
5.解:A、∠A=∠D,∠B=∠E,∠C=∠F是AAA,不能判定两三角形全等,故选项不符合题意;
B、AB=DE,BC=EF,∠A=∠D是SSA,不能判定两三角形全等,故选项不符合题意;
C、∠A=∠D,∠C=∠F,AC=DF符合ASA,能判定两三角形全等,故选项符合题意;
D、△ABC的周长等于△DEF的周长,三边不可能相等,故选项不符合题意.
故选:C.
6.解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣50°=130°,
∵BO平分∠ABC,CO平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=65°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣65°=115°.
故选:D.
7.解:由作图可知,OE=OD,EC=DC,
在△OCE和△OCD中,
,
∴△OCE≌△OCD(SSS),
∴∠COD=∠COE.
故选:D.
8.解:A、最大角∠C=×180°=90°,是直角三角形,不符合题意;
B、由∠A﹣∠C=∠B,可得∠A=∠B+∠C,
故最大角∠A=180°÷2=90°,是直角三角形,不符合题意;
C、设∠A=∠B=x,则∠C=x,
所以,x+x+x=180°,
解得x=72°,
最大角∠A=∠B=72°,是锐角三角形,符合题意;
D、设∠A=x,则∠B=2x,∠C=3x,
所以,x+2x+3x=180°,
解得x=30°,
最大角∠C=3×30°=90°,是直角三角形,不符合题意;
故选:C.
9.解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC,
∴S△BCE=S△ABC,
∵点F是CE的中点,
∴S△BEF=S△BCE=S△ABC,
∵△BEF的面积为3,
∴S△ABC=4×3=12.
故选:D.
10.解:如图所示:一共有7个符合题意的点.
故选:D.
二、填空题
11.解:一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是三角形的稳定性.
故答案为:三角形的稳定性.
12.解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5
∴x+y=11.
故答案为:11.
13.解:∵△ABC≌△DEF,
∴BC=20=EF,∠A=∠D=x,
∵∠B=50°,∠C=60°,
∴∠A=180°﹣50°﹣60°=70°,
∴x=70°,
故答案为:70°.
14.解:如图,
由题意得:∠2=30°,∠3=45°,
∴∠1=∠2+∠3=75°.
故答案为:75°.
15.解:若△AOP为直角三角形,则
①∠A=90°时,△AOP为直角三角形;
②当∠APO=90°时,△AOP为直角三角形,此时∠A=40°.
故答案为90°或40°.
三、解答题
16.证明:∵AD=BE,
∴AD﹣BD=BE﹣BD,
∴AB=ED,
∵AC∥EF,
∴∠A=∠E,
在△ABC和△EDF中,,
∴△ABC≌△EDF(AAS),
∴BC=DF.
17.证明:∵∠ACD=∠BCE,
∴∠ACB=∠DCE,
在△BCA和△ECD中,
,
∴△ABC≌△DEC(SAS),
∴∠A=∠D.
18.解:∵∠B=40°,∠C=62°,
∴∠BAC=180°﹣62°﹣40°=78°,
∵AE为∠BAC角平分线,
∴∠BAE=78°÷2=39°,
∵AD为△ABC的高,
∴∠ADB=90°,
∴∠DAC=90°﹣∠C=90°﹣62°=28°,
∴∠EAD=∠EAC﹣∠DAC=39°﹣28°=11°,
即∠EAD的度数是11°.
19.解:如图,△ABC和△ABC′为所作.
20.解:∵∠CPD=38°,∠APB=52°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=52°,
在△CPD和△PAB中
∵,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=33,PB=8,
∴AB=33﹣8=25(m),
答:楼高AB是25米.
21.(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°,
∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△ACE和△CBG中,
,
∴△ACE≌△CBG(ASA);
(2)解:(1)中结论成立,理由如下:
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△ACE和△CBG中,
,
∴△ACE≌△CBG(ASA);
(3)解:在Rt△ABC中,AC=BC,点D是AB的中点,
∴CD⊥AB,CD=AD=BD=AB=4,
∵BG=4,
∴BD=BG,
∴点G、E、F、D四点重合,
∴当点E运动到点D时,BG=4,此时AE的长为4.
