2022-2023学年人教版数学八年级上册 13.3 有一个角为30°的直角三角形 同步练习 (Word版,含答案)
文档属性
| 名称 | 2022-2023学年人教版数学八年级上册 13.3 有一个角为30°的直角三角形 同步练习 (Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 371.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 17:55:20 | ||
图片预览

文档简介
第12课 有一个角为30°的直角三角形
一、新课学习
在直角三角形中,30°角所对的直角边等于______________。
几何语言:
∵_________________,
∴__________________。
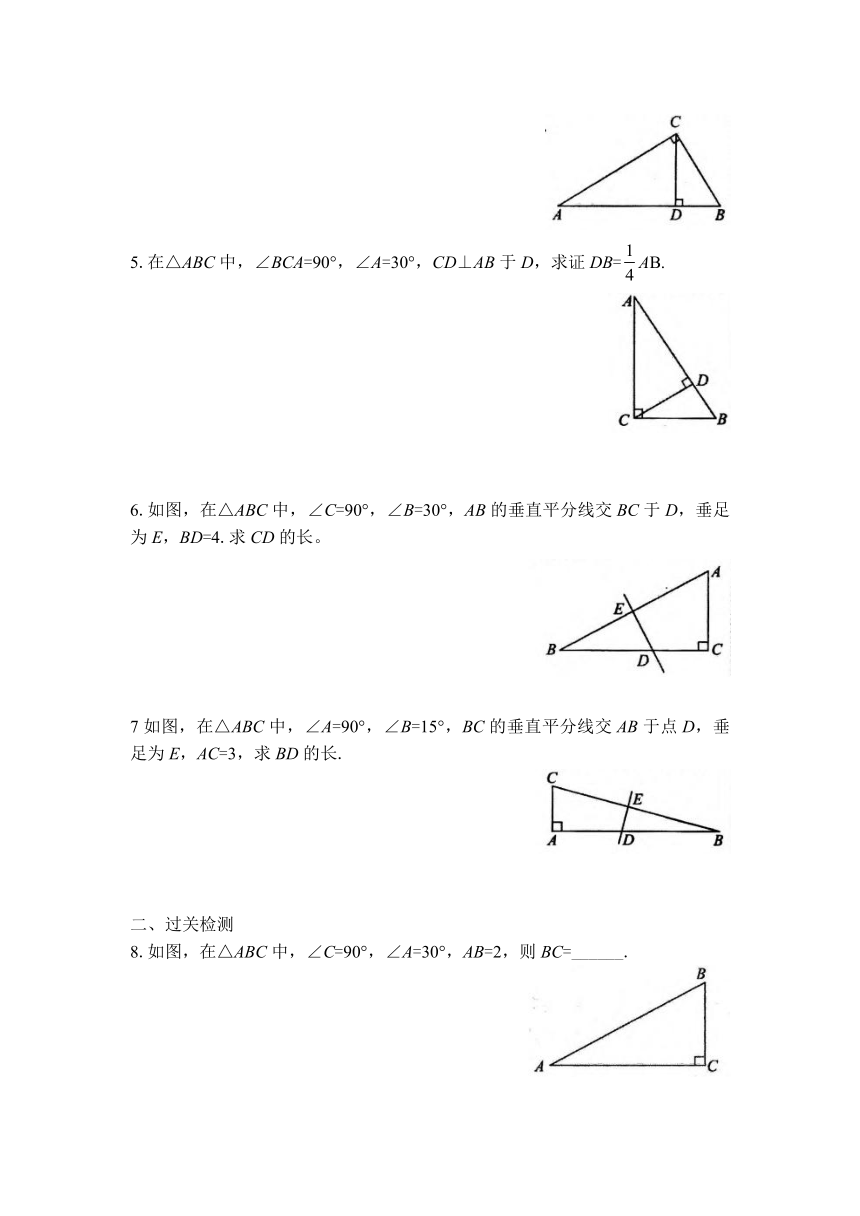
1.在△ABC中,∠C=90°.若∠B=60°,BC=3,求AB的长。
2如图,△ABC中,已知AB=AC,∠C=30°,AB⊥AD,AD=4.求:
求:(1)BD的长(2)BC的长。
3.如图,△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC.若BD=6,求AC的长。
4.在△ABC中,∠BCA=90°,∠A=30°,CD⊥AB于D,DB=2,求BC,AD的长.
5.在△ABC中,∠BCA=90°,∠A=30°,CD⊥AB于D,求证DB=AB.
6.如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4.求CD的长。
7如图,在△ABC中,∠A=90°,∠B=15°,BC的垂直平分线交AB于点D,垂足为E,AC=3,求BD的长.
二、过关检测
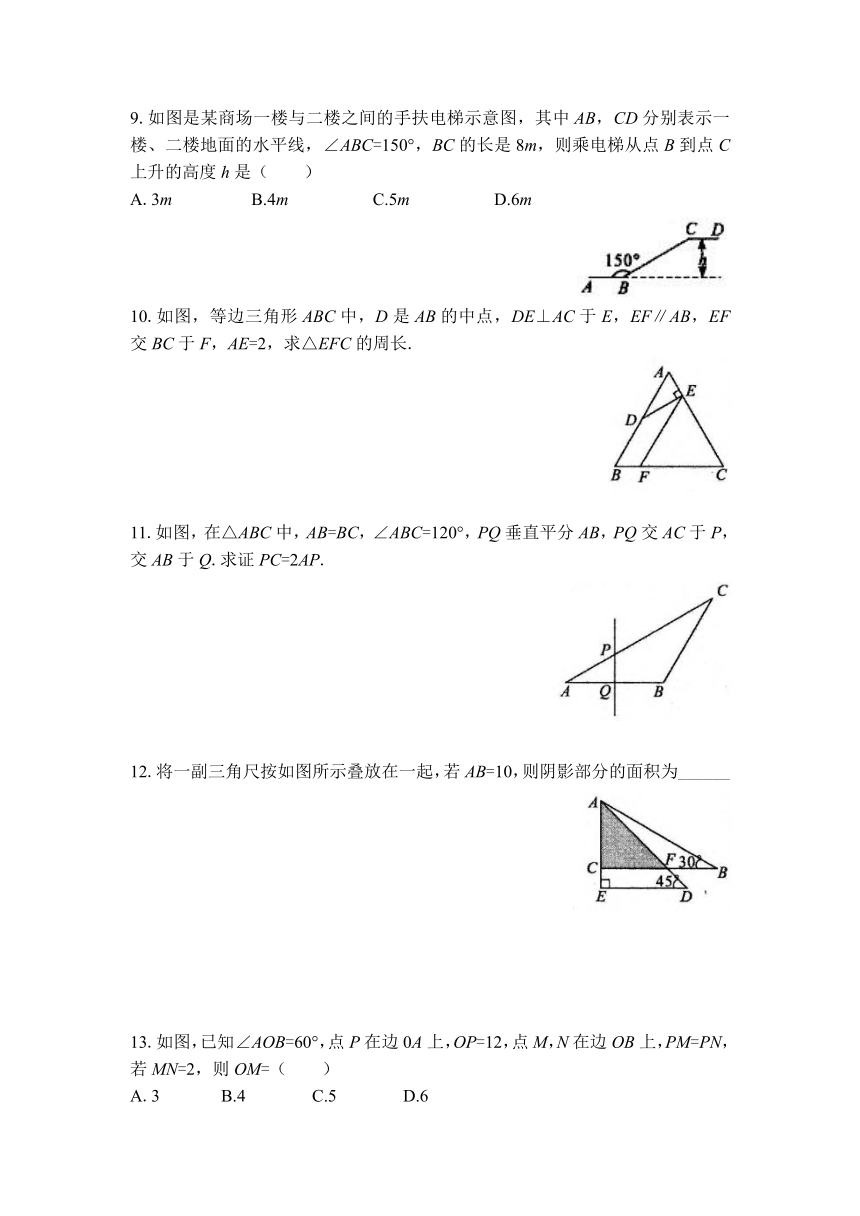
8.如图,在△ABC中,∠C=90°,∠A=30°,AB=2,则BC=______.
9.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.3m B.4m C.5m D.6m
10.如图,等边三角形ABC中,D是AB的中点,DE⊥AC于E,EF∥AB,EF交BC于F,AE=2,求△EFC的周长.
11.如图,在△ABC中,AB=BC,∠ABC=120°,PQ垂直平分AB,PQ交AC于P,交AB于Q.求证PC=2AP.
12.将一副三角尺按如图所示叠放在一起,若AB=10,则阴影部分的面积为______
13.如图,已知∠AOB=60°,点P在边0A上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A.3 B.4 C.5 D.6
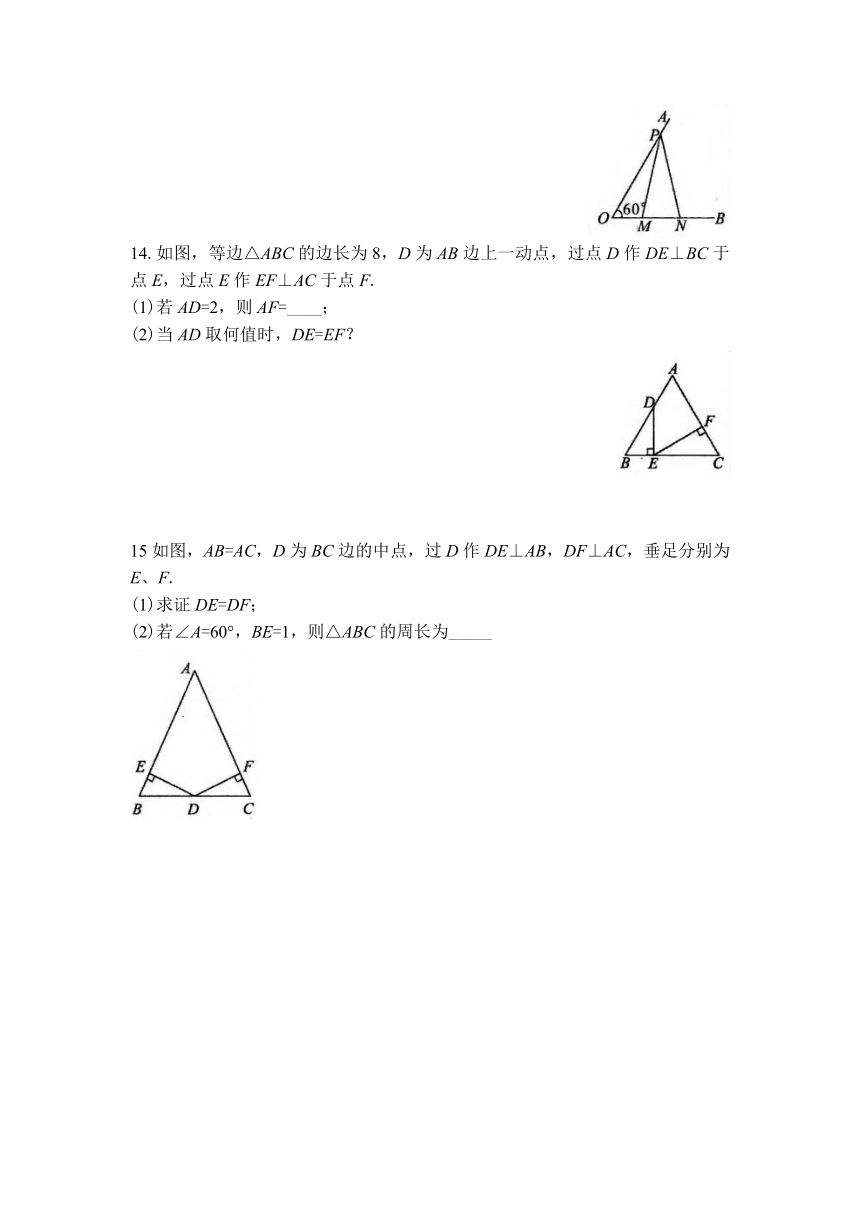
14.如图,等边△ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.
(1)若AD=2,则AF=____;
(2)当AD取何值时,DE=EF?
15如图,AB=AC,D为BC边的中点,过D作DE⊥AB,DF⊥AC,垂足分别为E、F.
(1)求证DE=DF;
(2)若∠A=60°,BE=1,则△ABC的周长为_____
第12课 有一个角为30°的直角三角形
1.解:∵∠C=90°,∠B=60°,
∴∠A=180°-90-60°=30°,
∴BC=3,,∴AB=2BC=6.
2.解:(1)∵AB=AC,∠C=30°,
∴∠B=∠C=30°.
又∵AB⊥AD,
∴BD=2AD=2×4=8.
(2)∵∠ADB=∠C+∠DAC=60°,
∴∠DAC=60°-∠C=30°.
∴DC=AD=4.
∴BC=BD+DC=8+4=12.
3.解:在△ABC中,∠C=90°,∠ABC=60°,∴∠A=30.
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠A=∠ABD,.AD=BD=6.
在Rt△BCD中,CD=BD=×6=3,
∴AC=AD+CD=6+3=9.
4.解:∵∠BCA=90°,∠A=30°,
∴∠B=180°-90°-30°=60°.
∴∠DCB=90°-60°=30°.
∴BC=2DB=2×2=4,
AB=2BC=2×4=8.
∴AD=AB-BD=8-2=6.
5.证明:∵∠A=30°,∠BCA=90°,
∴BC=AB,∠B=60°,
∵CD⊥AB,∴∠CDB=90°
∴∠BCD=90°-∠B=30°,
∴BD=BC,∴BD=-AB.
6.解:连接AD.
∵DE是线段AB的垂直平分线,
∴BD=AD,∠DAE=∠B=30°.
∴∠DAC=60°-30°=30°.
即AD为∠EAC的平分线.
∵DE⊥AE,DC⊥AC,
∴CD=DE=BD=×4=2.
7.解:如图,连接CD,
∵DE垂直平分BC,
∴DB=DC,
∴∠B=∠DCB=15°,
∴∠ADC=2×15°=30°,
∵∠A=90°,
∴CD=2AC=2×3=6,
∴BD=6.
8.1 9.B
10.解:∵∠A=60°,DE⊥AC,
∴∠ADE=30°.
∴AD=2AE=2×2=4.
∴AB=2AD=2×4=8.
∴EC=AC-AE=8-2=6.
又∵EF//AB,
∴∠EFC=∠B=60°,∠CEF=∠A=60°,
∴∠EFC=∠CEF=∠C=60°.
∴△EFC为等边三角形.
∴△EFC的周长为3×6=18.
11.证明:连接BP.
∵AB=BC,∠ABC=120°.
∴∠A=∠C
=×(180°-120°)=30°.
又∵PQ垂直平分AB.
∴∠PBQ=∠A=30°,AP=BP.
∴∠PBC=120°-∠PBQ=90°.
∴PC=2BP=2AP.
12.12.5 提示:AC=CF=AB=5.
13.C提示:过P作PQ⊥MN,垂足为Q.则有OM+MN=OP=×12=6.
∴OM=6-MN=6-×2=5.
14.解:(1):∵AB=8,AD=2
∴BD=AB-AD=6
在Rt△BDE中
∠BDE=90°-∠B=30°
∴BE=BD=3
∴CE=BC-BE=5
在Rt△CFE中
∠CEF=90°-∠C=30°
∴CF=CE=,
∴AF=AC-FC=
故答案为
(2)在△BDE和△CEF中,
∴△BDE≌△CEF(AAS)
∴BE=CF
∴BE=CF=EC
∴BE=BC=,
∴BD=2BE=
∴AD=AB-BD=
∴AD=时,DE=EF.
15.(1)证明:连接AD.
∵AB=AC,D为BC边的中点.
∴AD为∠BAC的平分线.
又∵DE⊥AB,DF⊥AC.
∴DE=DF.
(2)解:∵∠A=60°,AB=AC,
∴∠BAD=∠CAD=30°,△ABC为等边三角形,
∴∠BDE=90°-∠B=90°-60°=30°.
∴BD=2BE=2,
∴AB=2BD=2×2=4.
∴△ABC的周长为3×4=12.
故答案为12.
一、新课学习
在直角三角形中,30°角所对的直角边等于______________。
几何语言:
∵_________________,
∴__________________。
1.在△ABC中,∠C=90°.若∠B=60°,BC=3,求AB的长。
2如图,△ABC中,已知AB=AC,∠C=30°,AB⊥AD,AD=4.求:
求:(1)BD的长(2)BC的长。
3.如图,△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC.若BD=6,求AC的长。
4.在△ABC中,∠BCA=90°,∠A=30°,CD⊥AB于D,DB=2,求BC,AD的长.
5.在△ABC中,∠BCA=90°,∠A=30°,CD⊥AB于D,求证DB=AB.
6.如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线交BC于D,垂足为E,BD=4.求CD的长。
7如图,在△ABC中,∠A=90°,∠B=15°,BC的垂直平分线交AB于点D,垂足为E,AC=3,求BD的长.
二、过关检测
8.如图,在△ABC中,∠C=90°,∠A=30°,AB=2,则BC=______.
9.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.3m B.4m C.5m D.6m
10.如图,等边三角形ABC中,D是AB的中点,DE⊥AC于E,EF∥AB,EF交BC于F,AE=2,求△EFC的周长.
11.如图,在△ABC中,AB=BC,∠ABC=120°,PQ垂直平分AB,PQ交AC于P,交AB于Q.求证PC=2AP.
12.将一副三角尺按如图所示叠放在一起,若AB=10,则阴影部分的面积为______
13.如图,已知∠AOB=60°,点P在边0A上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A.3 B.4 C.5 D.6
14.如图,等边△ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.
(1)若AD=2,则AF=____;
(2)当AD取何值时,DE=EF?
15如图,AB=AC,D为BC边的中点,过D作DE⊥AB,DF⊥AC,垂足分别为E、F.
(1)求证DE=DF;
(2)若∠A=60°,BE=1,则△ABC的周长为_____
第12课 有一个角为30°的直角三角形
1.解:∵∠C=90°,∠B=60°,
∴∠A=180°-90-60°=30°,
∴BC=3,,∴AB=2BC=6.
2.解:(1)∵AB=AC,∠C=30°,
∴∠B=∠C=30°.
又∵AB⊥AD,
∴BD=2AD=2×4=8.
(2)∵∠ADB=∠C+∠DAC=60°,
∴∠DAC=60°-∠C=30°.
∴DC=AD=4.
∴BC=BD+DC=8+4=12.
3.解:在△ABC中,∠C=90°,∠ABC=60°,∴∠A=30.
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠A=∠ABD,.AD=BD=6.
在Rt△BCD中,CD=BD=×6=3,
∴AC=AD+CD=6+3=9.
4.解:∵∠BCA=90°,∠A=30°,
∴∠B=180°-90°-30°=60°.
∴∠DCB=90°-60°=30°.
∴BC=2DB=2×2=4,
AB=2BC=2×4=8.
∴AD=AB-BD=8-2=6.
5.证明:∵∠A=30°,∠BCA=90°,
∴BC=AB,∠B=60°,
∵CD⊥AB,∴∠CDB=90°
∴∠BCD=90°-∠B=30°,
∴BD=BC,∴BD=-AB.
6.解:连接AD.
∵DE是线段AB的垂直平分线,
∴BD=AD,∠DAE=∠B=30°.
∴∠DAC=60°-30°=30°.
即AD为∠EAC的平分线.
∵DE⊥AE,DC⊥AC,
∴CD=DE=BD=×4=2.
7.解:如图,连接CD,
∵DE垂直平分BC,
∴DB=DC,
∴∠B=∠DCB=15°,
∴∠ADC=2×15°=30°,
∵∠A=90°,
∴CD=2AC=2×3=6,
∴BD=6.
8.1 9.B
10.解:∵∠A=60°,DE⊥AC,
∴∠ADE=30°.
∴AD=2AE=2×2=4.
∴AB=2AD=2×4=8.
∴EC=AC-AE=8-2=6.
又∵EF//AB,
∴∠EFC=∠B=60°,∠CEF=∠A=60°,
∴∠EFC=∠CEF=∠C=60°.
∴△EFC为等边三角形.
∴△EFC的周长为3×6=18.
11.证明:连接BP.
∵AB=BC,∠ABC=120°.
∴∠A=∠C
=×(180°-120°)=30°.
又∵PQ垂直平分AB.
∴∠PBQ=∠A=30°,AP=BP.
∴∠PBC=120°-∠PBQ=90°.
∴PC=2BP=2AP.
12.12.5 提示:AC=CF=AB=5.
13.C提示:过P作PQ⊥MN,垂足为Q.则有OM+MN=OP=×12=6.
∴OM=6-MN=6-×2=5.
14.解:(1):∵AB=8,AD=2
∴BD=AB-AD=6
在Rt△BDE中
∠BDE=90°-∠B=30°
∴BE=BD=3
∴CE=BC-BE=5
在Rt△CFE中
∠CEF=90°-∠C=30°
∴CF=CE=,
∴AF=AC-FC=
故答案为
(2)在△BDE和△CEF中,
∴△BDE≌△CEF(AAS)
∴BE=CF
∴BE=CF=EC
∴BE=BC=,
∴BD=2BE=
∴AD=AB-BD=
∴AD=时,DE=EF.
15.(1)证明:连接AD.
∵AB=AC,D为BC边的中点.
∴AD为∠BAC的平分线.
又∵DE⊥AB,DF⊥AC.
∴DE=DF.
(2)解:∵∠A=60°,AB=AC,
∴∠BAD=∠CAD=30°,△ABC为等边三角形,
∴∠BDE=90°-∠B=90°-60°=30°.
∴BD=2BE=2,
∴AB=2BD=2×2=4.
∴△ABC的周长为3×4=12.
故答案为12.
