4.1.1 立体图形与平面图形 教案
图片预览



文档简介
中小学教育资源及组卷应用平台
4.1.1 立体图形与平面图形 教学设计
课题 4.1.1 立体图形与平面图形 单元 第4 单元 学科 数学 年级 七年级(上)
教材分析 理解几何图形的定义,能从实物中抽象出对应的几何图形。会将几何图形分类,能找到立体图形和平面图形的关系.
核心素养分析 经历观察、思考、分析的过程,培养学生用图形描述现实世界的意识,激发学生对几何图形的好奇心,培养几何直觉.
学习目标 1.认识一些简单的几何图形(长方体、正方体、棱柱、棱锥、圆柱、圆锥、球等立体图形以及简单的平面图形),能识别这些几何图形,并能用自己的语言描述图形的特征.2.使学生能根据平面展开图初步判断和制作与展开立体图形,体会立体图形与平面图形之间的关系.
重点 认识简单的平面图形和立体图形,发展几何直觉.
难点 从具体事物中抽象出几何图形是难点.
教学过程
教学环节 教师活动 学生活动 设计意图
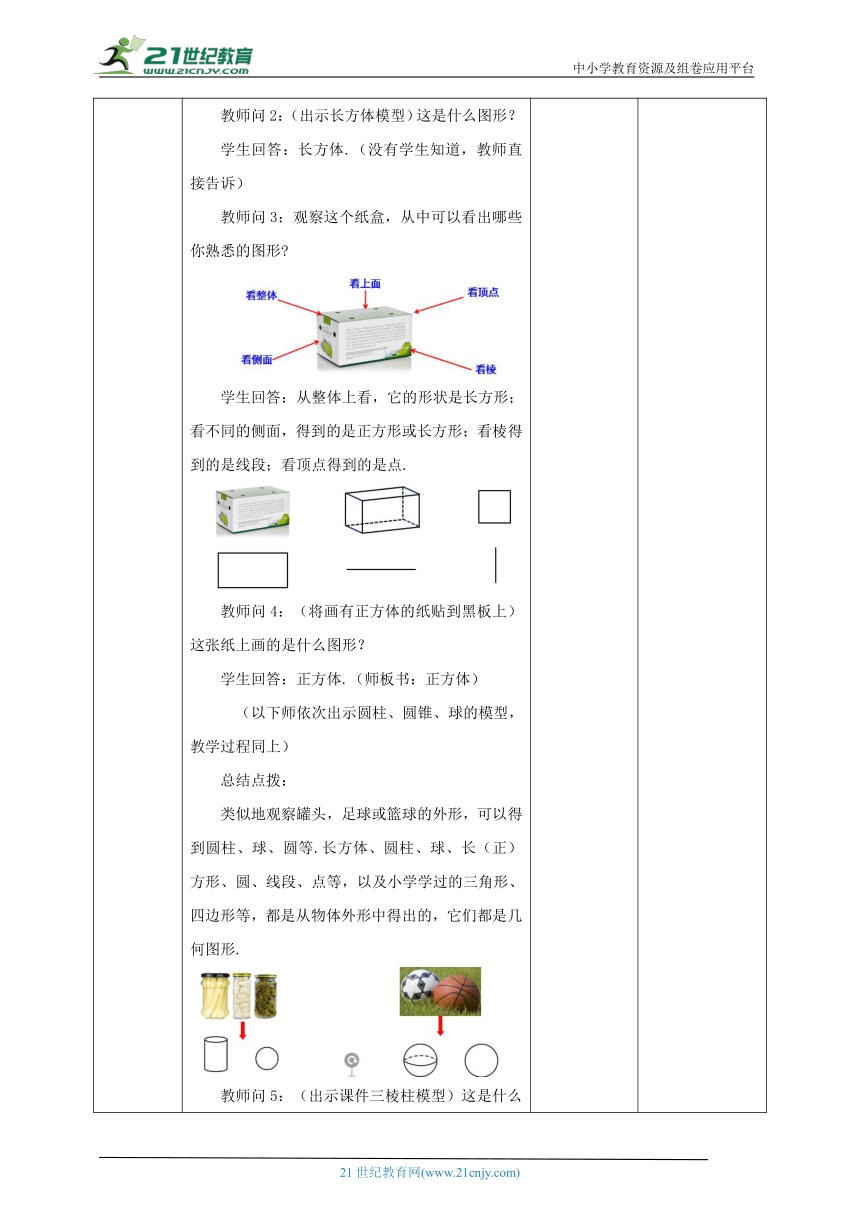
学生回答:从整体上看,它的形状是长方形;看不同的侧面,得到的是正方形或长方形;看棱得到的是线段;看顶点得到的是点.
类似地观察罐头,足球或篮球的外形,可以得到圆柱、球、圆等.长方体、圆柱、球、长(正)方形、圆、线段、点等,以及小学学过的三角形、四边形等,都是从物体外形中得出的,它们都是几何图形.
教师问5:(出示课件三棱柱模型)这是什么图形?师生共同解答如下:这个图形叫棱柱.教师问6:(将画有三棱柱的纸贴到黑板上)这张纸上画的是什么图形?学生回答:棱柱.(师板书:棱柱)教师问7:(出示六棱柱模型)这又是什么图形?学生回答:这个图形也是棱柱.教师问8:(将画有六棱柱的纸贴到黑板上)这张纸上画的是什么图形?学生回答:棱柱.(师板书:棱柱)教师问9:(三棱柱、六棱柱的棱垂直桌面放置)这两个图形都是棱柱,但它们的形状还是有不一样的地方,有什么不一样的地方?师生共同解答如下:(演示三棱柱)这个棱柱相对的这两个面都是三角形,(演示六棱柱)这个棱柱相对的这两个面都是六边形,所以我们把这个棱柱叫做三棱柱,(板书:三)把这个棱柱叫做六棱柱.(板书:六)教师问10:(三棱柱的棱平行桌面放置)三棱柱像我们生活中见过的什么东西?学生回答:……(多让几位同学说)三棱柱挺像是一个帐篷.教师问11:(六棱柱的棱垂直桌面放置)六棱柱像我们生活中的什么东西?学生回答:……(多让几位同学说)六棱柱挺像是一个茶叶盒.(也可说其它东西) (以下师依次出示四棱锥、圆锥,教学过程与棱柱教学基本相同)教师问12:(指模型)刚才我们看了正方体、长方体、圆柱、圆锥、球、棱柱、棱锥,这些图形有什么共同的特点呢?师生共同解答如下:它们都是立体图形.(板书:立体图形)总结点拨:这些几何图形的各部分不都在同一平面内,它们是立体图形.教师问13:(指板书)这些立体图形在我们生活中都是常见的,请大家把课本翻到115页,(稍停)上面一排印了一些实物,这些实物是什么东西?学生回答:地球仪、魔方、现代汉语词典、沙堆、铅笔、建筑物.教师问14:这些实物是什么立体图形呢?请大家把实物与下面一排的图形用线连起来.学生回答:生连线,给出答案.教师问15:(指板书)正方体、长方体、圆柱、圆锥、球、棱柱、棱锥都是立体图形. 观察小茗的房间,说说你能看到哪些立体图形.学生回答:……(多让几位同学发表看法)教师问16:(出示两个模型的组合图形,譬如将正方体与圆锥组合在一起)这个图形是立体图形吗?学生讨论后回答:是立体图形.教师问17:(出示三个模型的组合图形)这个图形是立体图形吗?学生回答:是立体图形.教师问18:(出示四个模型的组合图形)这个图形是立体图形吗?学生回答:是立体图形.教师总结:这些图形都是立体图形,将一些立体图形组合在一起,我们可以得到各种各样的立体图形.实际上,只要图形的各部分不都在同一个平面内,也就是说图形不是平平的,这样的图形都是立体图形.一棵树可以看成是一个立体图形,一朵花可以看成是一个立体图形,一只藏羚羊可以看成是一个立体图形,雄伟的布达拉宫可以看成是一个立体图形,甚至整座城市也可以看成是一个立体图形.教师问19:棱锥与棱柱的区别是什么?学生讨论后回答:棱柱的两个底面形状相同,大小相等,棱锥只有一个底面,所有侧棱交于一点.棱柱的侧面时长方形,棱锥的侧面是三角形.教师问20:圆锥与圆柱的区别是什么?学生回答:圆柱的两个底面都是圆且相等,圆锥只有一个底面是圆和一个顶点.教师问21:根据已有的数学经验,我们能否把它们进行分类?你的标准是什么?学生回答:合理即可。(答案不唯一)总结点拨:多媒体演示庐山景观,请学生背诵苏东坡《题西林壁》并说说诗中意境.跨越学科界限,以苏东坡的诗《题西林壁》“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”营造一个崭新的数学学习氛围,并从中挖掘蕴含的数学道理.比一比讲台上依次放置粉笔盒、乒乓球、热水瓶.请四位学生上来后按照不同的方位站好,然后向同学们汇报各自看到的情形.探究1 分别从正面、左面、上面观察乒乓球、粉笔盒、茶叶盒,各能得到什么平面图形?(出示实物)让学生从不同方向观察立体图形,体验立体图形转化为平面图形的过程.长方体、圆锥分别从正面、左面、上面观察,各能得到什么图形?试着画一画.(出示实物)这样,我们将立体图形转化成了平面图形,以四人小组为学习单位进行小组创作,培养学生的观察力和创新能力.教科书第117页图4.1-7,从正面、左面、上面观察得到的平面图形你能画出来吗?适当变动正方体的摆放位置,你还能解决吗?探究2 (1)出示教材第118页图4.1-9的平面展开图,让学生说一说这是什么立体图形?教师让学生回答,若学生对此有困难,可让学生自己动手画一画,剪一剪,仔细体会.(2)让学生拿出自己的墨水盒或其他正方体方盒,动手剪一剪,看能得到几种正方体的展开图. 思考自议欣赏相关图片,看后学生感触很深,有一种被震撼的感觉,同时也对几何产生了浓厚的兴趣. 各小组交流,合作,畅所欲言,同学们通过认真观察,发现自己的身边有许多自己熟悉的几何图形.
讲授新课 提炼概念 典例精讲有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展成平面图形.这样的平面图形称为相应立体图形的展开图.小组赛 将正方体的表面适当剪开,看它的展开图是怎样的结构,比一比,看哪一组得到的结果多!归纳:共有11种基本情况 学生回答不全,教师补充。能由实物形状想象出几何图形,由几何图形想象出实物形状,进一步丰富对几何形状的感性认识. 初步了解立体图形和平面图形的关系。对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.
课堂练习 四、巩固训练 1.关于几何研究的内容,下列说法正确的是( ) A. 几何只研究物体的形状 B. 几何只研究物体的大小 C. 几何只研究物体的位置关系 D. 几何研究的内容包括物体的形状、大小和位置关系D2.一个几何体及从正面和上面看到它的图形如图所示,那么从左面看到的图形正确的是( )B3.如图是一个带有方形空洞和圆形空洞的儿童玩具.如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )B4.观察图中的几何体,并按要求填空:(1)若把上面7个几何体分成两类:把①③⑥⑦分为一类,是因为组成这些几何体的面是____________;而把②④⑤分为另一类,是因为组成这些几何体的面中有___________.(2)若把上面7个几何体分成两类:___________为第一类,都属于柱体; ___________为第二类,都属于____体; ____为第三类,都属于球体.5. (1)把图中的立体图形分类,并说明分类标准. (2)图中③与⑥各有什么特征?有哪些相同点和不同点?解:(1)按柱体、锥体、球体分类: ①③⑤⑥⑦为柱体;④⑧为锥体; ②为球体. (2)③是圆柱,圆柱的上、下底面都是圆,侧面是一个曲面; ⑥是五 棱柱,上、下底面是形状、大小相同的五边形,侧面是5个长方形, 侧面的个数与底面边数相等. 相同点:两者都有两个底面. 不同点:圆柱的底面是圆,五棱柱的底面是五边形;圆柱的侧面是一个曲面,五棱柱的侧面由5个长方形组成.6.用小正方体搭一个几何体,使得从正面、上面看它所得到的图形如图
所示,搭成这样的一个几何体,最少需要多少个小正方体?最多需要
多少个小正方体?并分别画出所对应情况的几何体从左面看所得到的图形 .解:最少需要小正方体的个数为8个.最多需要小正方体的个数为11个.由此可画出在所需小正方体个数最少时的四种情况下的几何体从左面看所得到的图形如答图(a). 当所需小正方体个数最多时,对应的几何体从左面看所得到的图形如答图(b).
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
4.1.1 立体图形与平面图形 教学设计
课题 4.1.1 立体图形与平面图形 单元 第4 单元 学科 数学 年级 七年级(上)
教材分析 理解几何图形的定义,能从实物中抽象出对应的几何图形。会将几何图形分类,能找到立体图形和平面图形的关系.
核心素养分析 经历观察、思考、分析的过程,培养学生用图形描述现实世界的意识,激发学生对几何图形的好奇心,培养几何直觉.
学习目标 1.认识一些简单的几何图形(长方体、正方体、棱柱、棱锥、圆柱、圆锥、球等立体图形以及简单的平面图形),能识别这些几何图形,并能用自己的语言描述图形的特征.2.使学生能根据平面展开图初步判断和制作与展开立体图形,体会立体图形与平面图形之间的关系.
重点 认识简单的平面图形和立体图形,发展几何直觉.
难点 从具体事物中抽象出几何图形是难点.
教学过程
教学环节 教师活动 学生活动 设计意图
学生回答:从整体上看,它的形状是长方形;看不同的侧面,得到的是正方形或长方形;看棱得到的是线段;看顶点得到的是点.
类似地观察罐头,足球或篮球的外形,可以得到圆柱、球、圆等.长方体、圆柱、球、长(正)方形、圆、线段、点等,以及小学学过的三角形、四边形等,都是从物体外形中得出的,它们都是几何图形.
教师问5:(出示课件三棱柱模型)这是什么图形?师生共同解答如下:这个图形叫棱柱.教师问6:(将画有三棱柱的纸贴到黑板上)这张纸上画的是什么图形?学生回答:棱柱.(师板书:棱柱)教师问7:(出示六棱柱模型)这又是什么图形?学生回答:这个图形也是棱柱.教师问8:(将画有六棱柱的纸贴到黑板上)这张纸上画的是什么图形?学生回答:棱柱.(师板书:棱柱)教师问9:(三棱柱、六棱柱的棱垂直桌面放置)这两个图形都是棱柱,但它们的形状还是有不一样的地方,有什么不一样的地方?师生共同解答如下:(演示三棱柱)这个棱柱相对的这两个面都是三角形,(演示六棱柱)这个棱柱相对的这两个面都是六边形,所以我们把这个棱柱叫做三棱柱,(板书:三)把这个棱柱叫做六棱柱.(板书:六)教师问10:(三棱柱的棱平行桌面放置)三棱柱像我们生活中见过的什么东西?学生回答:……(多让几位同学说)三棱柱挺像是一个帐篷.教师问11:(六棱柱的棱垂直桌面放置)六棱柱像我们生活中的什么东西?学生回答:……(多让几位同学说)六棱柱挺像是一个茶叶盒.(也可说其它东西) (以下师依次出示四棱锥、圆锥,教学过程与棱柱教学基本相同)教师问12:(指模型)刚才我们看了正方体、长方体、圆柱、圆锥、球、棱柱、棱锥,这些图形有什么共同的特点呢?师生共同解答如下:它们都是立体图形.(板书:立体图形)总结点拨:这些几何图形的各部分不都在同一平面内,它们是立体图形.教师问13:(指板书)这些立体图形在我们生活中都是常见的,请大家把课本翻到115页,(稍停)上面一排印了一些实物,这些实物是什么东西?学生回答:地球仪、魔方、现代汉语词典、沙堆、铅笔、建筑物.教师问14:这些实物是什么立体图形呢?请大家把实物与下面一排的图形用线连起来.学生回答:生连线,给出答案.教师问15:(指板书)正方体、长方体、圆柱、圆锥、球、棱柱、棱锥都是立体图形. 观察小茗的房间,说说你能看到哪些立体图形.学生回答:……(多让几位同学发表看法)教师问16:(出示两个模型的组合图形,譬如将正方体与圆锥组合在一起)这个图形是立体图形吗?学生讨论后回答:是立体图形.教师问17:(出示三个模型的组合图形)这个图形是立体图形吗?学生回答:是立体图形.教师问18:(出示四个模型的组合图形)这个图形是立体图形吗?学生回答:是立体图形.教师总结:这些图形都是立体图形,将一些立体图形组合在一起,我们可以得到各种各样的立体图形.实际上,只要图形的各部分不都在同一个平面内,也就是说图形不是平平的,这样的图形都是立体图形.一棵树可以看成是一个立体图形,一朵花可以看成是一个立体图形,一只藏羚羊可以看成是一个立体图形,雄伟的布达拉宫可以看成是一个立体图形,甚至整座城市也可以看成是一个立体图形.教师问19:棱锥与棱柱的区别是什么?学生讨论后回答:棱柱的两个底面形状相同,大小相等,棱锥只有一个底面,所有侧棱交于一点.棱柱的侧面时长方形,棱锥的侧面是三角形.教师问20:圆锥与圆柱的区别是什么?学生回答:圆柱的两个底面都是圆且相等,圆锥只有一个底面是圆和一个顶点.教师问21:根据已有的数学经验,我们能否把它们进行分类?你的标准是什么?学生回答:合理即可。(答案不唯一)总结点拨:多媒体演示庐山景观,请学生背诵苏东坡《题西林壁》并说说诗中意境.跨越学科界限,以苏东坡的诗《题西林壁》“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”营造一个崭新的数学学习氛围,并从中挖掘蕴含的数学道理.比一比讲台上依次放置粉笔盒、乒乓球、热水瓶.请四位学生上来后按照不同的方位站好,然后向同学们汇报各自看到的情形.探究1 分别从正面、左面、上面观察乒乓球、粉笔盒、茶叶盒,各能得到什么平面图形?(出示实物)让学生从不同方向观察立体图形,体验立体图形转化为平面图形的过程.长方体、圆锥分别从正面、左面、上面观察,各能得到什么图形?试着画一画.(出示实物)这样,我们将立体图形转化成了平面图形,以四人小组为学习单位进行小组创作,培养学生的观察力和创新能力.教科书第117页图4.1-7,从正面、左面、上面观察得到的平面图形你能画出来吗?适当变动正方体的摆放位置,你还能解决吗?探究2 (1)出示教材第118页图4.1-9的平面展开图,让学生说一说这是什么立体图形?教师让学生回答,若学生对此有困难,可让学生自己动手画一画,剪一剪,仔细体会.(2)让学生拿出自己的墨水盒或其他正方体方盒,动手剪一剪,看能得到几种正方体的展开图. 思考自议欣赏相关图片,看后学生感触很深,有一种被震撼的感觉,同时也对几何产生了浓厚的兴趣. 各小组交流,合作,畅所欲言,同学们通过认真观察,发现自己的身边有许多自己熟悉的几何图形.
讲授新课 提炼概念 典例精讲有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展成平面图形.这样的平面图形称为相应立体图形的展开图.小组赛 将正方体的表面适当剪开,看它的展开图是怎样的结构,比一比,看哪一组得到的结果多!归纳:共有11种基本情况 学生回答不全,教师补充。能由实物形状想象出几何图形,由几何图形想象出实物形状,进一步丰富对几何形状的感性认识. 初步了解立体图形和平面图形的关系。对于一些立体图形的问题,常把它们转化为平面图形来研究和处理.
课堂练习 四、巩固训练 1.关于几何研究的内容,下列说法正确的是( ) A. 几何只研究物体的形状 B. 几何只研究物体的大小 C. 几何只研究物体的位置关系 D. 几何研究的内容包括物体的形状、大小和位置关系D2.一个几何体及从正面和上面看到它的图形如图所示,那么从左面看到的图形正确的是( )B3.如图是一个带有方形空洞和圆形空洞的儿童玩具.如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )B4.观察图中的几何体,并按要求填空:(1)若把上面7个几何体分成两类:把①③⑥⑦分为一类,是因为组成这些几何体的面是____________;而把②④⑤分为另一类,是因为组成这些几何体的面中有___________.(2)若把上面7个几何体分成两类:___________为第一类,都属于柱体; ___________为第二类,都属于____体; ____为第三类,都属于球体.5. (1)把图中的立体图形分类,并说明分类标准. (2)图中③与⑥各有什么特征?有哪些相同点和不同点?解:(1)按柱体、锥体、球体分类: ①③⑤⑥⑦为柱体;④⑧为锥体; ②为球体. (2)③是圆柱,圆柱的上、下底面都是圆,侧面是一个曲面; ⑥是五 棱柱,上、下底面是形状、大小相同的五边形,侧面是5个长方形, 侧面的个数与底面边数相等. 相同点:两者都有两个底面. 不同点:圆柱的底面是圆,五棱柱的底面是五边形;圆柱的侧面是一个曲面,五棱柱的侧面由5个长方形组成.6.用小正方体搭一个几何体,使得从正面、上面看它所得到的图形如图
所示,搭成这样的一个几何体,最少需要多少个小正方体?最多需要
多少个小正方体?并分别画出所对应情况的几何体从左面看所得到的图形 .解:最少需要小正方体的个数为8个.最多需要小正方体的个数为11个.由此可画出在所需小正方体个数最少时的四种情况下的几何体从左面看所得到的图形如答图(a). 当所需小正方体个数最多时,对应的几何体从左面看所得到的图形如答图(b).
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
