数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.1.1倾斜角与斜率(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 937.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 12:47:14 | ||
图片预览






文档简介
(共18张PPT)
在几何问题研究中,我们常常直接依据几何图形中点、直线、平面的关系研究几何图形的性质.现在,我们采用另外一种研究方法:坐标法.坐标法是以坐标系为桥梁,把几何问题转化为代数问题,通过代数运算研究几何图形性质的方法。它是解析几何中最基本的研究方法.
本章首先在平面直角坐标系中,建立直线的方程。然后通过方程,研究直线的有关性质,如平行、垂直、两条直线的交点、点到直线的距离等。
思考1: 确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线 l ,如何利用坐标系确定它的位置?
x
y
O
l
①两点确定一条直线
②一点和一个方向也可以确定一条直线
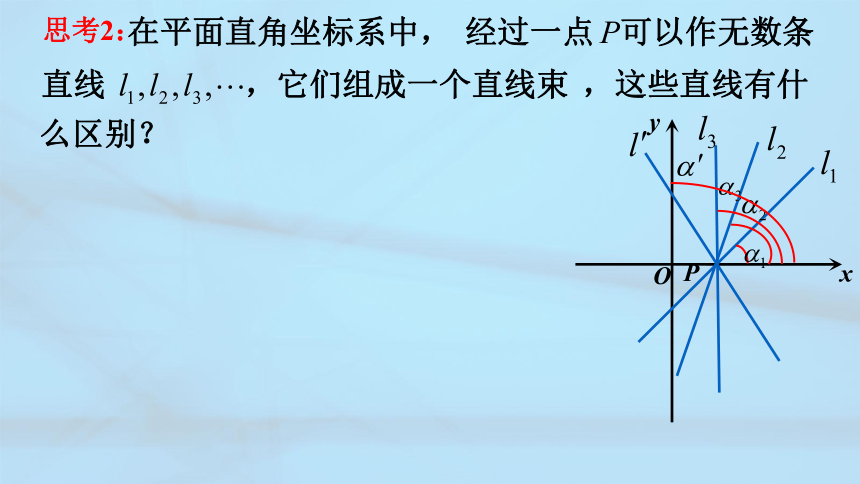
思考2:
x
y
O
P
一、直线的倾斜角
注: 平面内的任意一条直线都有确定的倾斜角α,其取值范围为:
当直线l与x轴相交时,我们取x轴为基准,x轴的正方向与直线l向上方向之间所成的角α叫做直线l的倾斜角.
规定:当直线l与x轴平行或重合时,它的倾斜角为0°.
【即时练习1】
1. 如图,△AOB是等腰直角三角形,则直线OA、OB、AB的倾斜角分别为
二、斜率
x
y
O
x
y
O
二、斜率
斜率
注: (1) 任何一条直线都有倾斜角, 但不一定有斜率.
(2) 直线的斜率反映直线的倾斜程度.
x
y
o
1. 若直线的倾斜角为60°,则它的斜率为_______;
若直线的斜率k=-1,则它的倾斜角为__________
2. 若图中的直线l1,l2,l3的斜率分别为k1,k2,k3,则k1,k2,k3的大小关系为_______________.
【即时练习2】
三、直线的方向向量与斜率的关系
x
y
O
l
1. 当m=____时,经过A(-m,6),B(1,3m)的直线的斜率是12.
【即时练习3】
2. 当m=_____时,经过A(m,2),B(-m,-2m-1),的直线的倾斜角为60°。
【变式训练】
课堂小结
在几何问题研究中,我们常常直接依据几何图形中点、直线、平面的关系研究几何图形的性质.现在,我们采用另外一种研究方法:坐标法.坐标法是以坐标系为桥梁,把几何问题转化为代数问题,通过代数运算研究几何图形性质的方法。它是解析几何中最基本的研究方法.
本章首先在平面直角坐标系中,建立直线的方程。然后通过方程,研究直线的有关性质,如平行、垂直、两条直线的交点、点到直线的距离等。
思考1: 确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线 l ,如何利用坐标系确定它的位置?
x
y
O
l
①两点确定一条直线
②一点和一个方向也可以确定一条直线
思考2:
x
y
O
P
一、直线的倾斜角
注: 平面内的任意一条直线都有确定的倾斜角α,其取值范围为:
当直线l与x轴相交时,我们取x轴为基准,x轴的正方向与直线l向上方向之间所成的角α叫做直线l的倾斜角.
规定:当直线l与x轴平行或重合时,它的倾斜角为0°.
【即时练习1】
1. 如图,△AOB是等腰直角三角形,则直线OA、OB、AB的倾斜角分别为
二、斜率
x
y
O
x
y
O
二、斜率
斜率
注: (1) 任何一条直线都有倾斜角, 但不一定有斜率.
(2) 直线的斜率反映直线的倾斜程度.
x
y
o
1. 若直线的倾斜角为60°,则它的斜率为_______;
若直线的斜率k=-1,则它的倾斜角为__________
2. 若图中的直线l1,l2,l3的斜率分别为k1,k2,k3,则k1,k2,k3的大小关系为_______________.
【即时练习2】
三、直线的方向向量与斜率的关系
x
y
O
l
1. 当m=____时,经过A(-m,6),B(1,3m)的直线的斜率是12.
【即时练习3】
2. 当m=_____时,经过A(m,2),B(-m,-2m-1),的直线的倾斜角为60°。
【变式训练】
课堂小结
