【新课标】1.1.2探索勾股定理 课件(共22张PPT)
文档属性
| 名称 | 【新课标】1.1.2探索勾股定理 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
1.1.2探索勾股定理
北师版八年级上册
教学目标
1.掌握用面积法如何验证勾股定理,并能应用勾股定理解决一些实际问题。
2.经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想。
复习旧知
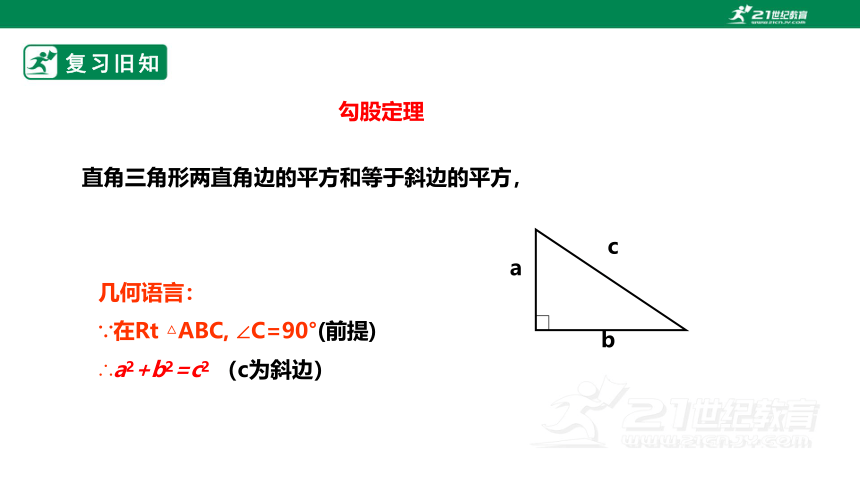
勾股定理
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,
情境导入
上一节课,我们通过测量和数格子的方法发现了勾股定理.在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
做一做
为了计算图1中大正方形的面积,小明对这个大正方形适当割补后得到图2、图3.
图1
图3
图2
新知讲解
(1)将所有三角形和正方形的面积用a,b,c的关系式表示出来;
(2) 图2、图3中正方形ABCD的面积分别是多少?你们有哪些表示方式?与同伴进行交流.
(3)你能分别利用图2、图3验证勾股定理吗?
据不完全统计,验证的方法有400多种,你有自己的方法吗?
新知讲解
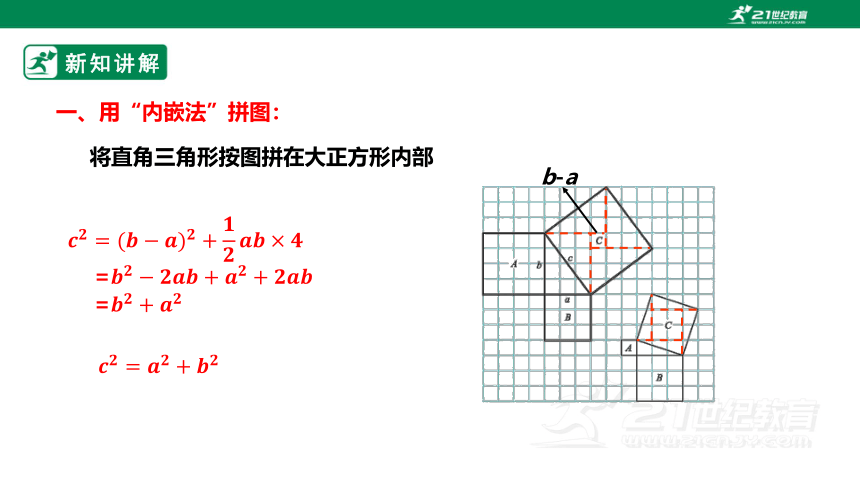
一、用“内嵌法”拼图:
将直角三角形按图拼在大正方形内部
b-a
=
=
新知讲解
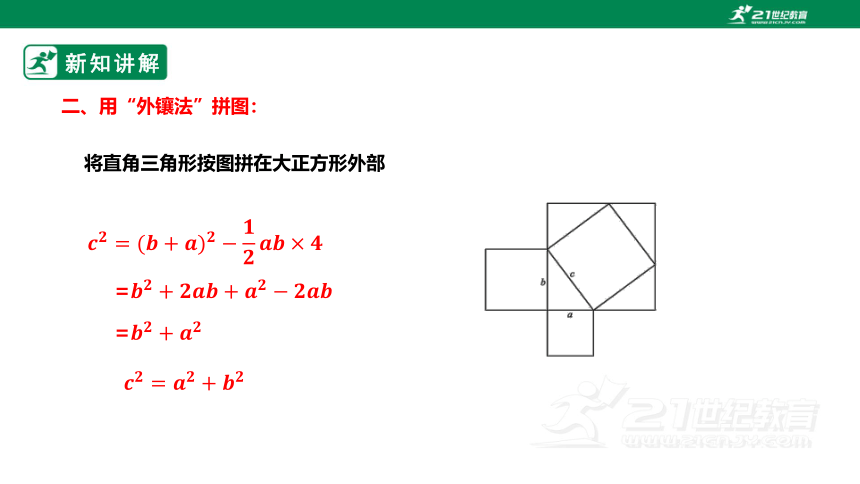
二、用“外镶法”拼图:
将直角三角形按图拼在大正方形外部
=
=
新知讲解
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
三、“总统证明法”
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
新知归纳
1.“勾股定理”的验证方法:
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
2.通过拼图证明勾股定理的思路:
(1)图形经过割补拼接后,只要没有重叠,没有空隙,面积就不会改变;
(2)根据同一种图形的面积的不同表示方法列出等式;
(3)利用等式性质变换验证结论成立.
即拼出图形→写出图形面积的表达式→找出等量关系→恒等变形→ 推导命题结论.
典例精析
例:我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
公路
B
C
A
400m
500m
解:由勾股定理,可以得到AB2=BC2+AC2,也就是5002=BC2+4002,所以BC=300.敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m),即它行驶的速度为108km/h.
议一议
观察下图,判断图中三角形的三边长是否满足a2+b2=c2.
A的面积 SA B的面积 SB C的面积
SC
图1
图2
8
9
29
5
8
9
课堂练习
1.用四个边长均为a,b,c的直角三角板,拼成如图所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2-2ab+b2 D.c2=(a+b)2
2.如图,一个长为2.5 m的梯子,一端放在离墙脚
1.5 m处,另一端靠墙,则梯子顶端距离墙脚( )
A.0.2 m B.0.4 m C.2 m D.4 m
A
C
课堂练习
3.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_________.
200m2
课堂练习
4.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4 m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2 m,则小巷的宽度为 。
2.2 m
课堂练习
5.两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米?
课堂练习
解:根据题意画出示意图,如图所示,
两棵树的高度分别为AB=8 m,CD=2 m,
两棵树之间的距离BD=8 m,
过点C作CE⊥AB,垂足为E,连接AC.
则BE=CD=2 m,EC=BD=8 m,
AE=AB-BE=8-2=6(m).
在Rt△ACE中,由勾股定理,得AC2=AE2+EC2,
即AC2=62+82=100,所以AC=10 m.
答:这只小鸟至少要飞10 m.
课堂总结
本节课你学到了什么?
知识:勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么.
方法:观察—猜想—探究—验证—归纳—应用;
思想:1. 特殊—一般
2. 数形结合思想
3. 方程的思想
板书设计
1.1.2探索勾股定理
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么.
作业布置
【必做题】
教材第6页练习题1题。
【选做题】
教材第7页习题1.2的1、2、3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.1.2探索勾股定理
北师版八年级上册
教学目标
1.掌握用面积法如何验证勾股定理,并能应用勾股定理解决一些实际问题。
2.经历勾股定理的验证过程,体会数形结合的思想和从特殊到一般的思想。
复习旧知
勾股定理
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,
情境导入
上一节课,我们通过测量和数格子的方法发现了勾股定理.在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
做一做
为了计算图1中大正方形的面积,小明对这个大正方形适当割补后得到图2、图3.
图1
图3
图2
新知讲解
(1)将所有三角形和正方形的面积用a,b,c的关系式表示出来;
(2) 图2、图3中正方形ABCD的面积分别是多少?你们有哪些表示方式?与同伴进行交流.
(3)你能分别利用图2、图3验证勾股定理吗?
据不完全统计,验证的方法有400多种,你有自己的方法吗?
新知讲解
一、用“内嵌法”拼图:
将直角三角形按图拼在大正方形内部
b-a
=
=
新知讲解
二、用“外镶法”拼图:
将直角三角形按图拼在大正方形外部
=
=
新知讲解
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
三、“总统证明法”
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
新知归纳
1.“勾股定理”的验证方法:
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
2.通过拼图证明勾股定理的思路:
(1)图形经过割补拼接后,只要没有重叠,没有空隙,面积就不会改变;
(2)根据同一种图形的面积的不同表示方法列出等式;
(3)利用等式性质变换验证结论成立.
即拼出图形→写出图形面积的表达式→找出等量关系→恒等变形→ 推导命题结论.
典例精析
例:我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
公路
B
C
A
400m
500m
解:由勾股定理,可以得到AB2=BC2+AC2,也就是5002=BC2+4002,所以BC=300.敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m),即它行驶的速度为108km/h.
议一议
观察下图,判断图中三角形的三边长是否满足a2+b2=c2.
A的面积 SA B的面积 SB C的面积
SC
图1
图2
8
9
29
5
8
9
课堂练习
1.用四个边长均为a,b,c的直角三角板,拼成如图所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2
C.c2=a2-2ab+b2 D.c2=(a+b)2
2.如图,一个长为2.5 m的梯子,一端放在离墙脚
1.5 m处,另一端靠墙,则梯子顶端距离墙脚( )
A.0.2 m B.0.4 m C.2 m D.4 m
A
C
课堂练习
3.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_________.
200m2
课堂练习
4.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7 m,顶端距离地面2.4 m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2 m,则小巷的宽度为 。
2.2 m
课堂练习
5.两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米?
课堂练习
解:根据题意画出示意图,如图所示,
两棵树的高度分别为AB=8 m,CD=2 m,
两棵树之间的距离BD=8 m,
过点C作CE⊥AB,垂足为E,连接AC.
则BE=CD=2 m,EC=BD=8 m,
AE=AB-BE=8-2=6(m).
在Rt△ACE中,由勾股定理,得AC2=AE2+EC2,
即AC2=62+82=100,所以AC=10 m.
答:这只小鸟至少要飞10 m.
课堂总结
本节课你学到了什么?
知识:勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么.
方法:观察—猜想—探究—验证—归纳—应用;
思想:1. 特殊—一般
2. 数形结合思想
3. 方程的思想
板书设计
1.1.2探索勾股定理
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么.
作业布置
【必做题】
教材第6页练习题1题。
【选做题】
教材第7页习题1.2的1、2、3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
