【新课标】1.2一定是直角三角形吗? 课件(共21张PPT)
文档属性
| 名称 | 【新课标】1.2一定是直角三角形吗? 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
1.2一定是直角三角形吗?
北师版八年级上册
教学目标
1.探索和掌握勾股定理的逆定理,并能理解勾股数的概念。
2.经历证明勾股定理的逆定理的过程,能利用勾股定理的逆定理判断一个三角形是直角三角形。
情境导入
∵在Rt △ABC, ∠C=90°
∴a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方
a
b
c
A
C
B
问题:在一个直角三角形中三条边满足什么样的关系?
思考:如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是否就是直角三角形呢?
若在 △ABC, a2+b2=c2
则 ∠C=90°吗?
a
b
c
A
C
B
做一做
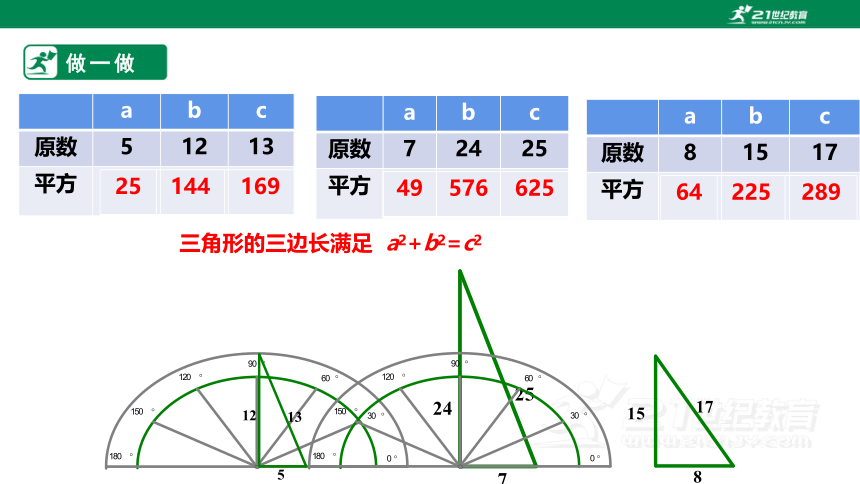
下面的每组数分别是一个三角形的三边长a,b,c 而且都满足a2+b2=c2:3,4,5;5,12,13;7,24,25;8,15,17。 分别以每组数为三边长画出三角形,它们都是直角三角形吗?你是怎么想的?与同伴进行交流.
做一做
a b c
原数 7 24 25
平方
a b c
原数 5 12 13
平方
a b c
原数 8 15 17
平方
49 576 625
25 144 169
64 225 289
三角形的三边长满足 a2+b2=c2
新知讲解
我觉得这个猜想不准确,因为测量结果可能有误差.
我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
据此你有什么猜想呢
由上面几个例子,我们猜想:
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
新知讲解
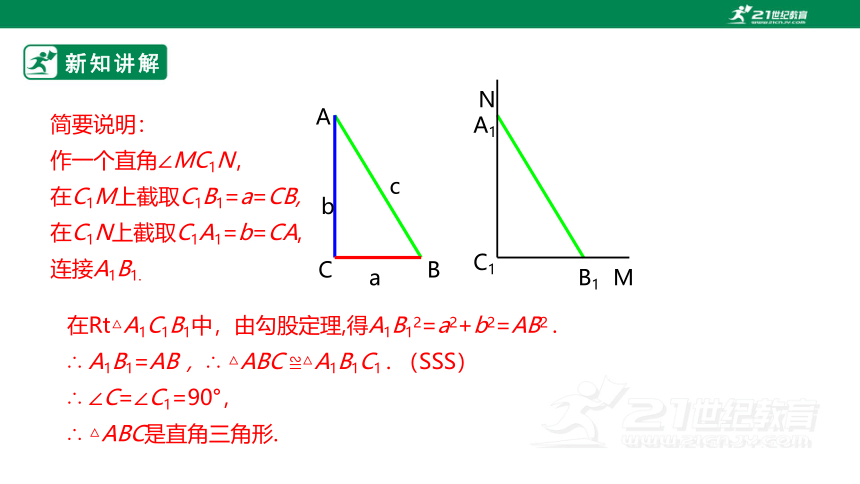
简要说明:
作一个直角∠MC1N,
在C1M上截取C1B1=a=CB,
在C1N上截取C1A1=b=CA,
连接A1B1.
在Rt△A1C1B1中,由勾股定理,得A1B12=a2+b2=AB2 .
∴ A1B1=AB ,∴ △ABC ≌△A1B1C1 . (SSS)
∴ ∠C=∠C1=90°,
∴ △ABC是直角三角形.
c
A
C
B
b
a
C1
M
N
B1
A1
归纳总结
几何语言:
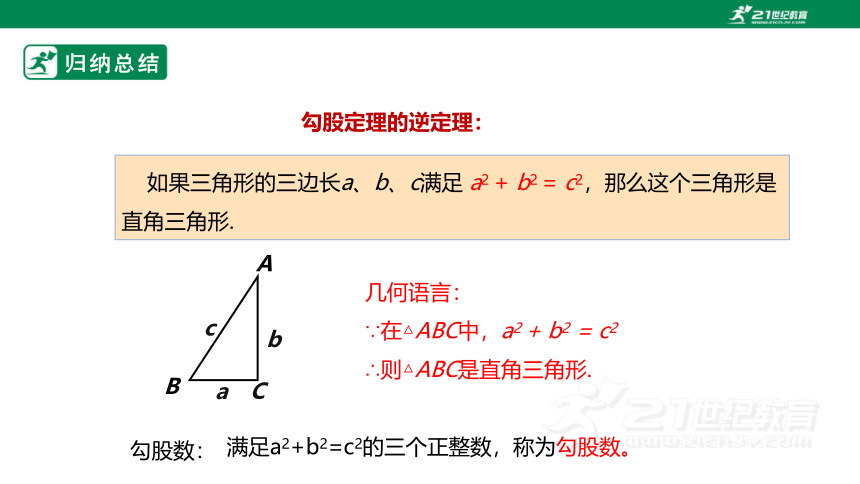
∵在△ABC中,a2 + b2 = c2
∴则△ABC是直角三角形.
如果三角形的三边长a、b、c满足 a2 + b2 = c2,那么这个三角形是直角三角形.
b
c
C
a
B
A
勾股定理的逆定理:
勾股数:
满足a2+b2=c2的三个正整数,称为勾股数。
新知讲解
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角 ,最长边所对角为直角.
特别说明:
典例精析
例 一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
图2
图1
典例精析
解:在△ABD中,AB 2+AD 2=9+16=25=BD 2,
所以△ABD是直角三角形,∠A是直角.
在△BCD中,BD 2+BC 2=25+144=169=CD 2,
所以△BCD是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
课堂练习
1. 下列各组数是勾股数的是( )
A. 3,4,5 B. 1. 5,2,2. 5
C. 32,42,52 D. ,,
2. 在△ABC中,AB=8,AC=15,BC=17,则该三角形
为( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰直角三角形
A
B
课堂练习
3. △ABC的三边分别是a,b,c且满足|a-8 |+(b-6)2=0,则当c2=__________时,△ABC是直角三角形.
4.如图,点O为数轴的原点,点A和B分别对应的实数是﹣1和1.过点B作BC⊥AB,以点B为圆心,OB长为半径画弧,交BC于点D;以点A为圆心,AD长为半径画弧,交数轴于点E,则点E对应的实数是_____ .
100或28
课堂练习
5.绿都农场有一块菜地如图所示,现测得AB=12m,BC=13m,CD=4m,AD=3m,∠D=90°,求这块菜地的面积.
课堂练习
解: 如图,连接AC,
∵CD=4m,AD=3m,∠D=90°,
∴AC==
∴SRt△ADC= =6m2.
在△CAB中,AC=5m,AB=12m,BC=13m,
∴ ,
∴△CAB为直角三角形,且∠CAB=90°,
∴SRt△CAB==30m2
课堂练习
6. 如图,在△ABC中,∠ABC=∠C,AC=3,D是CA延长线上一点,AD=5,BD=4. 求证:AB⊥BD.
证明:∵∠ABC=∠C,AC=3,
∴AB=AC=3.
∵AD=5,BD=4,
∴AB2+BD2=25=AD2.
∴△ABD是直角三角形,且∠ABD=90°.
∴AB⊥BD.
课堂总结
勾股定理的逆定理
逆定理
如何判断
直角三角形
如果三角形的三边长a、 b 、 c 满足,那么这个三角形是直角三角形.
①找最长边
②算两短边的平方和与长边的平方
③判断等量关系
本节课你学到了什么?
板书设计
1.如果三角形的三边长a,b,c满足a2 +b2=c2,那么这个三角形是直角三角形.
2.勾股数:满足a2 +b2=c2的三个正整数,称为勾股数.
1.2一定是直角三角形吗?
作业布置
【必做题】
教材第10页练习题1题。
【选做题】
教材第10页习题1.3的1、2、3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2一定是直角三角形吗?
北师版八年级上册
教学目标
1.探索和掌握勾股定理的逆定理,并能理解勾股数的概念。
2.经历证明勾股定理的逆定理的过程,能利用勾股定理的逆定理判断一个三角形是直角三角形。
情境导入
∵在Rt △ABC, ∠C=90°
∴a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方
a
b
c
A
C
B
问题:在一个直角三角形中三条边满足什么样的关系?
思考:如果一个三角形中有两边的平方和等于第三边的平方,那么这个三角形是否就是直角三角形呢?
若在 △ABC, a2+b2=c2
则 ∠C=90°吗?
a
b
c
A
C
B
做一做
下面的每组数分别是一个三角形的三边长a,b,c 而且都满足a2+b2=c2:3,4,5;5,12,13;7,24,25;8,15,17。 分别以每组数为三边长画出三角形,它们都是直角三角形吗?你是怎么想的?与同伴进行交流.
做一做
a b c
原数 7 24 25
平方
a b c
原数 5 12 13
平方
a b c
原数 8 15 17
平方
49 576 625
25 144 169
64 225 289
三角形的三边长满足 a2+b2=c2
新知讲解
我觉得这个猜想不准确,因为测量结果可能有误差.
我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
据此你有什么猜想呢
由上面几个例子,我们猜想:
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
新知讲解
简要说明:
作一个直角∠MC1N,
在C1M上截取C1B1=a=CB,
在C1N上截取C1A1=b=CA,
连接A1B1.
在Rt△A1C1B1中,由勾股定理,得A1B12=a2+b2=AB2 .
∴ A1B1=AB ,∴ △ABC ≌△A1B1C1 . (SSS)
∴ ∠C=∠C1=90°,
∴ △ABC是直角三角形.
c
A
C
B
b
a
C1
M
N
B1
A1
归纳总结
几何语言:
∵在△ABC中,a2 + b2 = c2
∴则△ABC是直角三角形.
如果三角形的三边长a、b、c满足 a2 + b2 = c2,那么这个三角形是直角三角形.
b
c
C
a
B
A
勾股定理的逆定理:
勾股数:
满足a2+b2=c2的三个正整数,称为勾股数。
新知讲解
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角 ,最长边所对角为直角.
特别说明:
典例精析
例 一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
图2
图1
典例精析
解:在△ABD中,AB 2+AD 2=9+16=25=BD 2,
所以△ABD是直角三角形,∠A是直角.
在△BCD中,BD 2+BC 2=25+144=169=CD 2,
所以△BCD是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
课堂练习
1. 下列各组数是勾股数的是( )
A. 3,4,5 B. 1. 5,2,2. 5
C. 32,42,52 D. ,,
2. 在△ABC中,AB=8,AC=15,BC=17,则该三角形
为( )
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 等腰直角三角形
A
B
课堂练习
3. △ABC的三边分别是a,b,c且满足|a-8 |+(b-6)2=0,则当c2=__________时,△ABC是直角三角形.
4.如图,点O为数轴的原点,点A和B分别对应的实数是﹣1和1.过点B作BC⊥AB,以点B为圆心,OB长为半径画弧,交BC于点D;以点A为圆心,AD长为半径画弧,交数轴于点E,则点E对应的实数是_____ .
100或28
课堂练习
5.绿都农场有一块菜地如图所示,现测得AB=12m,BC=13m,CD=4m,AD=3m,∠D=90°,求这块菜地的面积.
课堂练习
解: 如图,连接AC,
∵CD=4m,AD=3m,∠D=90°,
∴AC==
∴SRt△ADC= =6m2.
在△CAB中,AC=5m,AB=12m,BC=13m,
∴ ,
∴△CAB为直角三角形,且∠CAB=90°,
∴SRt△CAB==30m2
课堂练习
6. 如图,在△ABC中,∠ABC=∠C,AC=3,D是CA延长线上一点,AD=5,BD=4. 求证:AB⊥BD.
证明:∵∠ABC=∠C,AC=3,
∴AB=AC=3.
∵AD=5,BD=4,
∴AB2+BD2=25=AD2.
∴△ABD是直角三角形,且∠ABD=90°.
∴AB⊥BD.
课堂总结
勾股定理的逆定理
逆定理
如何判断
直角三角形
如果三角形的三边长a、 b 、 c 满足,那么这个三角形是直角三角形.
①找最长边
②算两短边的平方和与长边的平方
③判断等量关系
本节课你学到了什么?
板书设计
1.如果三角形的三边长a,b,c满足a2 +b2=c2,那么这个三角形是直角三角形.
2.勾股数:满足a2 +b2=c2的三个正整数,称为勾股数.
1.2一定是直角三角形吗?
作业布置
【必做题】
教材第10页练习题1题。
【选做题】
教材第10页习题1.3的1、2、3题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
