【核心素养目标】1.3勾股定理的应用 教学设计
文档属性
| 名称 | 【核心素养目标】1.3勾股定理的应用 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 14:02:56 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
1.3勾股定理的应用教学设计
课题 1.3勾股定理的应用 单元 1 学科 数学 年级 八
教材分析 本节是《勾股定理》第3节。具体内容是运用勾股定理及其逆定理解决简单的实际问题。当然,在这些具体问题的解决过程中,需要经历几何图形的抽象过程,需要借助观察、操作等实践活动,这些都有助于发展学生的分析问题、解决问题能力和应用意识;一些探究活动具有一定的难度,需要学生相互间的合作交流,有助于发展学生合作交流的能力。
核心素养分析 本节将利用勾股定理及其逆定理解决一些具体的实际问题,其中需要学生了解空间图形、对一些空间图形进行展开、折叠等活动。通过观察图形,探索图形间的关系,发展学生的空间观念,在将实际问题抽象成数学问题的过程中,提高分析问题、解决问题的能力及渗透数学建模的思想。在利用勾股定理解决实际问题的过程中,体验数学学习的实用性。
学习 目标 1.通过动手操作交流,会运用勾股定理求立体图形中两点之间的最短距离. 2.能够运用方程思想,利用勾股定理解决简单实际的问题,建立模型思想.
重点 利用建模思想构建直角三角形,利用勾股定理及逆定理,解决实际问题.
难点 能够运用勾股定理解决实际生活中的问题,建立模型思想.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 1、勾股定理的内容是什么? 2、勾股定理逆定理的内容是什么? 教师提问勾股定理与勾股定理逆定理知识点,由学生回答。 唤起学生的知识记忆,以便进入新的学习。
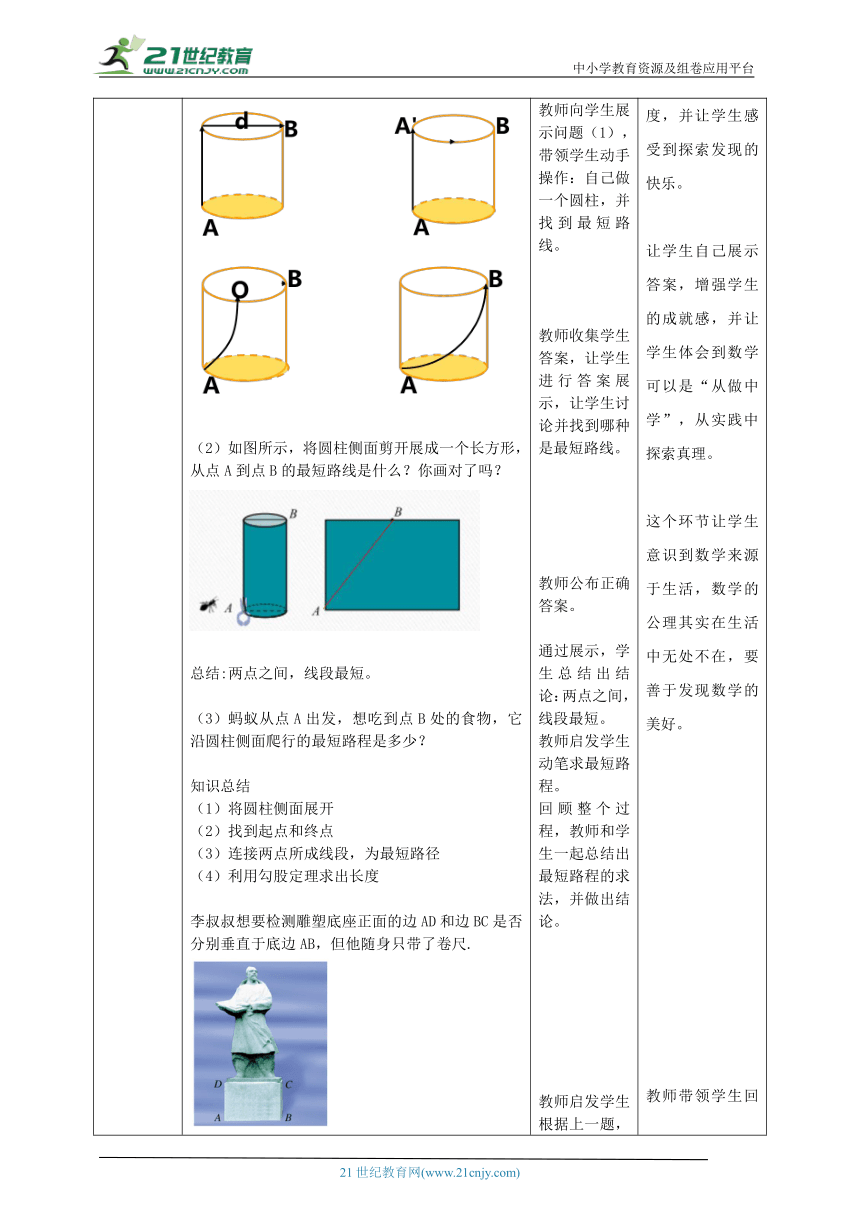
讲授新课 如图所示,有一个圆柱,它的高等于12cm,底面上圆的周长等于18cm.在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少? (1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面画出几条路线,你觉得哪条路线最短呢? (2)如图所示,将圆柱侧面剪开展成一个长方形,从点A到点B的最短路线是什么?你画对了吗? 总结:两点之间,线段最短。 蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱侧面爬行的最短路程是多少?
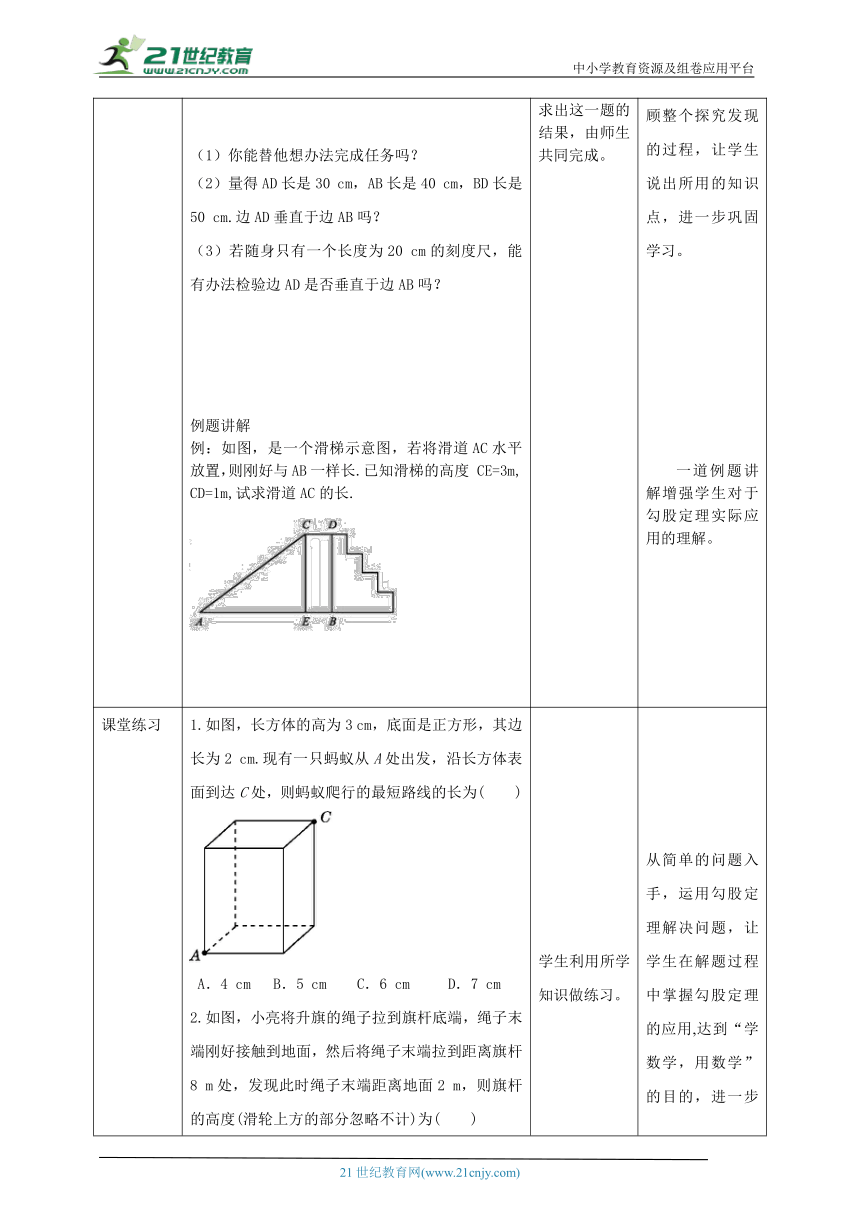
知识总结 将圆柱侧面展开 (2)找到起点和终点 (3)连接两点所成线段,为最短路径 (4)利用勾股定理求出长度 李叔叔想要检测雕塑底座正面的边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺. (1)你能替他想办法完成任务吗? 量得AD长是30 cm,AB长是40 cm,BD长是50 cm.边AD垂直于边AB吗? (3)若随身只有一个长度为20 cm的刻度尺,能有办法检验边AD是否垂直于边AB吗?
例题讲解 例:如图,是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度 CE=3m, CD=1m,试求滑道AC的长. 教师向学生展示问题,并读出题目。 教师向学生展示问题(1),带领学生动手操作:自己做一个圆柱,并找到最短路线。 教师收集学生答案,让学生进行答案展示,让学生讨论并找到哪种是最短路线。 教师公布正确答案。 通过展示,学生总结出结论:两点之间,线段最短。 教师启发学生动笔求最短路程。 回顾整个过程,教师和学生一起总结出最短路程的求法,并做出结论。 教师启发学生根据上一题,求出这一题的结果,由师生共同完成。 一道带有趣味性的题目,激起学生的思考,增强想要进一步探索问题的积极性。 教师通过启发,带领学生动手操作,大大提高学生的课堂参与度,并让学生感受到探索发现的快乐。 让学生自己展示答案,增强学生的成就感,并让学生体会到数学可以是“从做中学”,从实践中探索真理。 这个环节让学生意识到数学来源于生活,数学的公理其实在生活中无处不在,要善于发现数学的美好。 教师带领学生回顾整个探究发现的过程,让学生说出所用的知识点,进一步巩固学习。 一道例题讲解增强学生对于勾股定理实际应用的理解。
课堂练习 1.如图,长方体的高为3 cm,底面是正方形,其边长为2 cm.现有一只蚂蚁从A处出发,沿长方体表面到达C处,则蚂蚁爬行的最短路线的长为( ) A.4 cm B.5 cm C.6 cm D.7 cm 2.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为( ) A.12 m B.13 m C.16 m D.17 m 3.如图,已知∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=4,DE=EF=2,则AF的长是________. 4.如图,在一个高为3 m,长为5 m的楼梯表面铺地毯,则地毯长度为________. 5.小明想知道学校旗杆的高度,他把绳子一端挂在旗杆顶端,发现绳子垂到地面时还余1 m;当他把绳子下端拉开5 m后,绳子下端刚好接触地面,如图,你能帮他求出旗杆的高度吗 6.《中华人民共和国道路交通管理条例》规定:小汽车在城街路上行驶速度不得超过70km/h .如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪 处的正前方的30m处,过了 2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换: 1m/s=3.6km/h) 学生利用所学知识做练习。 从简单的问题入手,运用勾股定理解决问题,让学生在解题过程中掌握勾股定理的应用,达到“学数学,用数学”的目的,进一步培养学生解决问题的能力和推理论证的能力
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 通过小结让学生理清本节课的知识结构,感受探究过程中乐趣,体验克服困难的过程,树立学习数学的信心。
板书 1.3勾股定理的应用 本节课主要是应用勾股定理和它的逆定理来解决实际问题,在应用定理时,应注意: 1.没有图的要按题意画好图并标上字母; 2.不要用错定理.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.3勾股定理的应用教学设计
课题 1.3勾股定理的应用 单元 1 学科 数学 年级 八
教材分析 本节是《勾股定理》第3节。具体内容是运用勾股定理及其逆定理解决简单的实际问题。当然,在这些具体问题的解决过程中,需要经历几何图形的抽象过程,需要借助观察、操作等实践活动,这些都有助于发展学生的分析问题、解决问题能力和应用意识;一些探究活动具有一定的难度,需要学生相互间的合作交流,有助于发展学生合作交流的能力。
核心素养分析 本节将利用勾股定理及其逆定理解决一些具体的实际问题,其中需要学生了解空间图形、对一些空间图形进行展开、折叠等活动。通过观察图形,探索图形间的关系,发展学生的空间观念,在将实际问题抽象成数学问题的过程中,提高分析问题、解决问题的能力及渗透数学建模的思想。在利用勾股定理解决实际问题的过程中,体验数学学习的实用性。
学习 目标 1.通过动手操作交流,会运用勾股定理求立体图形中两点之间的最短距离. 2.能够运用方程思想,利用勾股定理解决简单实际的问题,建立模型思想.
重点 利用建模思想构建直角三角形,利用勾股定理及逆定理,解决实际问题.
难点 能够运用勾股定理解决实际生活中的问题,建立模型思想.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 1、勾股定理的内容是什么? 2、勾股定理逆定理的内容是什么? 教师提问勾股定理与勾股定理逆定理知识点,由学生回答。 唤起学生的知识记忆,以便进入新的学习。
讲授新课 如图所示,有一个圆柱,它的高等于12cm,底面上圆的周长等于18cm.在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少? (1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面画出几条路线,你觉得哪条路线最短呢? (2)如图所示,将圆柱侧面剪开展成一个长方形,从点A到点B的最短路线是什么?你画对了吗? 总结:两点之间,线段最短。 蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱侧面爬行的最短路程是多少?
知识总结 将圆柱侧面展开 (2)找到起点和终点 (3)连接两点所成线段,为最短路径 (4)利用勾股定理求出长度 李叔叔想要检测雕塑底座正面的边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺. (1)你能替他想办法完成任务吗? 量得AD长是30 cm,AB长是40 cm,BD长是50 cm.边AD垂直于边AB吗? (3)若随身只有一个长度为20 cm的刻度尺,能有办法检验边AD是否垂直于边AB吗?
例题讲解 例:如图,是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度 CE=3m, CD=1m,试求滑道AC的长. 教师向学生展示问题,并读出题目。 教师向学生展示问题(1),带领学生动手操作:自己做一个圆柱,并找到最短路线。 教师收集学生答案,让学生进行答案展示,让学生讨论并找到哪种是最短路线。 教师公布正确答案。 通过展示,学生总结出结论:两点之间,线段最短。 教师启发学生动笔求最短路程。 回顾整个过程,教师和学生一起总结出最短路程的求法,并做出结论。 教师启发学生根据上一题,求出这一题的结果,由师生共同完成。 一道带有趣味性的题目,激起学生的思考,增强想要进一步探索问题的积极性。 教师通过启发,带领学生动手操作,大大提高学生的课堂参与度,并让学生感受到探索发现的快乐。 让学生自己展示答案,增强学生的成就感,并让学生体会到数学可以是“从做中学”,从实践中探索真理。 这个环节让学生意识到数学来源于生活,数学的公理其实在生活中无处不在,要善于发现数学的美好。 教师带领学生回顾整个探究发现的过程,让学生说出所用的知识点,进一步巩固学习。 一道例题讲解增强学生对于勾股定理实际应用的理解。
课堂练习 1.如图,长方体的高为3 cm,底面是正方形,其边长为2 cm.现有一只蚂蚁从A处出发,沿长方体表面到达C处,则蚂蚁爬行的最短路线的长为( ) A.4 cm B.5 cm C.6 cm D.7 cm 2.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为( ) A.12 m B.13 m C.16 m D.17 m 3.如图,已知∠B=∠C=∠D=∠E=90°,且AB=CD=3,BC=4,DE=EF=2,则AF的长是________. 4.如图,在一个高为3 m,长为5 m的楼梯表面铺地毯,则地毯长度为________. 5.小明想知道学校旗杆的高度,他把绳子一端挂在旗杆顶端,发现绳子垂到地面时还余1 m;当他把绳子下端拉开5 m后,绳子下端刚好接触地面,如图,你能帮他求出旗杆的高度吗 6.《中华人民共和国道路交通管理条例》规定:小汽车在城街路上行驶速度不得超过70km/h .如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪 处的正前方的30m处,过了 2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换: 1m/s=3.6km/h) 学生利用所学知识做练习。 从简单的问题入手,运用勾股定理解决问题,让学生在解题过程中掌握勾股定理的应用,达到“学数学,用数学”的目的,进一步培养学生解决问题的能力和推理论证的能力
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 通过小结让学生理清本节课的知识结构,感受探究过程中乐趣,体验克服困难的过程,树立学习数学的信心。
板书 1.3勾股定理的应用 本节课主要是应用勾股定理和它的逆定理来解决实际问题,在应用定理时,应注意: 1.没有图的要按题意画好图并标上字母; 2.不要用错定理.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
