第三章 相互作用——力专项训练(一)-2022-2023学年高一上学期物理人教版(2019)必修第一册(word版含答案)
文档属性
| 名称 | 第三章 相互作用——力专项训练(一)-2022-2023学年高一上学期物理人教版(2019)必修第一册(word版含答案) | 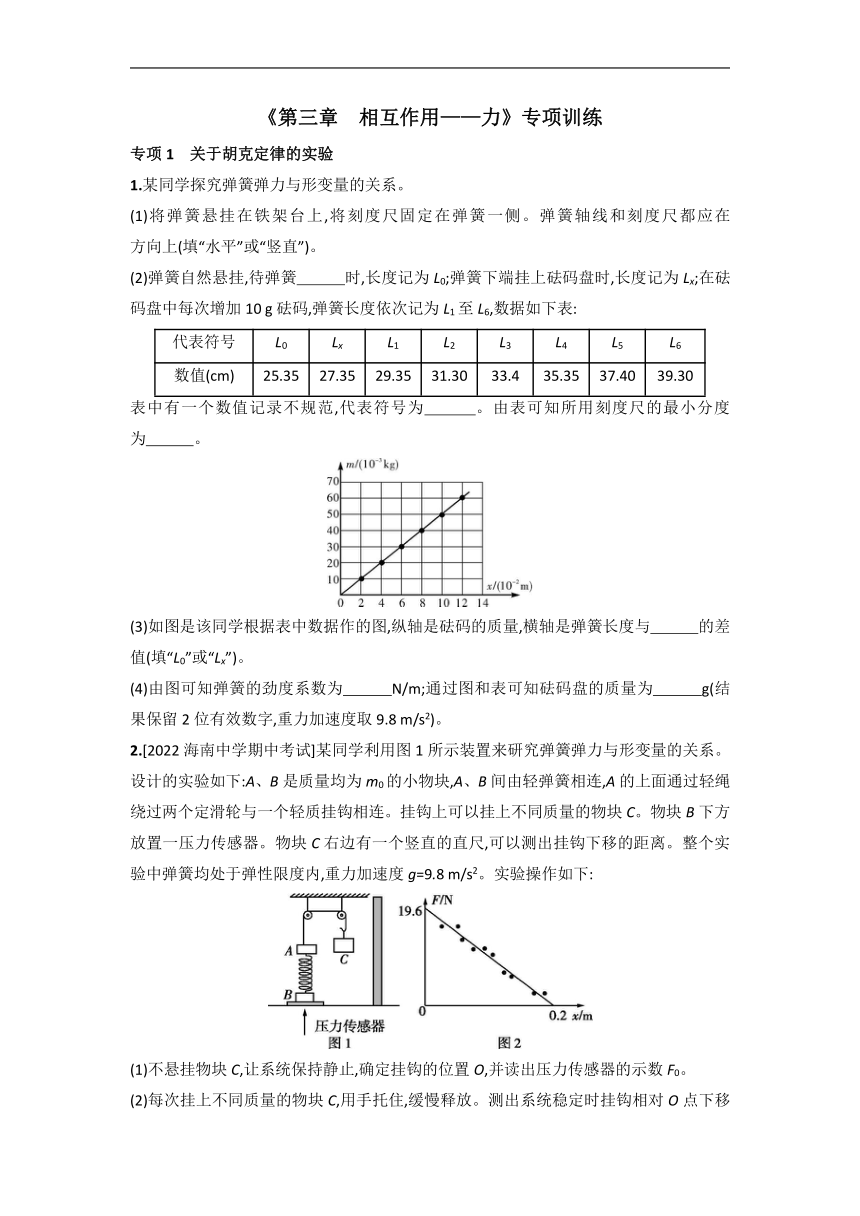 | |
| 格式 | docx | ||
| 文件大小 | 525.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-09-01 14:31:56 | ||
图片预览




文档简介
《第三章 相互作用——力》专项训练
专项1 关于胡克定律的实验
1.某同学探究弹簧弹力与形变量的关系。
(1)将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧。弹簧轴线和刻度尺都应在 方向上(填“水平”或“竖直”)。
(2)弹簧自然悬挂,待弹簧 时,长度记为L0;弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10 g砝码,弹簧长度依次记为L1至L6,数据如下表:
代表符号 L0 Lx L1 L2 L3 L4 L5 L6
数值(cm) 25.35 27.35 29.35 31.30 33.4 35.35 37.40 39.30
表中有一个数值记录不规范,代表符号为 。由表可知所用刻度尺的最小分度为 。
(3)如图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与 的差值(填“L0”或“Lx”)。
(4)由图可知弹簧的劲度系数为 N/m;通过图和表可知砝码盘的质量为 g(结果保留2位有效数字,重力加速度取9.8 m/s2)。
2.[2022海南中学期中考试]某同学利用图1所示装置来研究弹簧弹力与形变量的关系。设计的实验如下:A、B是质量均为m0的小物块,A、B间由轻弹簧相连,A的上面通过轻绳绕过两个定滑轮与一个轻质挂钩相连。挂钩上可以挂上不同质量的物块C。物块B下方放置一压力传感器。物块C右边有一个竖直的直尺,可以测出挂钩下移的距离。整个实验中弹簧均处于弹性限度内,重力加速度g=9.8 m/s2。实验操作如下:
(1)不悬挂物块C,让系统保持静止,确定挂钩的位置O,并读出压力传感器的示数F0。
(2)每次挂上不同质量的物块C,用手托住,缓慢释放。测出系统稳定时挂钩相对O点下移的距离xi,并读出相应的压力传感器的示数Fi。
(3)以压力传感器示数为纵坐标,挂钩下移距离为横坐标,根据每次测量的数据,描点作出F-x图像如图2所示。
①由图像可知,在实验误差允许的范围内,可以认为弹簧弹力与弹簧形变量成 (选填“正比”“反比”或“不确定关系”);
②由图像可知,弹簧劲度系数k= N/m。
3.[2022北京市十一学校期末考试]某同学在“探究弹力和弹簧伸长量的关系”时的实验装置如图所示,让刻度尺零刻度与弹簧上端齐平,弹簧不挂物体时下端指针所指的刻度为x0,在弹簧下用足够长的轻质细线挂上4个相同的钩码(弹簧处于弹性限度内),静止置于烧杯T内,控制阀门S通过细胶管向烧杯中缓慢注水,依次浸没4个钩码,记录每浸没一个钩码时指针所指的刻度分别为x1、x2、x3、x4,已知每个钩码的质量均为m,重力加速度为g,以xn为纵坐标,n为横坐标建立坐标系,作出xn和浸没钩码个数n的关系图像,求得图像斜率为a,纵截距为b,则该弹簧的劲度系数为 ,每个钩码所受浮力为 。(用a、b、m、g和x0表示)
4.[2021八省八校联考]2020年12月8日,中尼两国共同宣布了珠穆朗玛峰的最新高度为海拔8 848.86米,此次珠峰高度测量实现了北斗卫星导航系统首次应用、首次实测珠峰峰顶重力值等多项第一。同时,雪深探测雷达、重力仪、超长距离测距仪等一大批国产现代测量设备纷纷亮相。重力仪的内部包含了由弹簧组成的静力平衡系统。为测量某弹簧的劲度系数,某探究小组设计了如下实验。实验装置如图甲所示,角度传感器与可转动“T”形螺杆相连,“T”形螺杆上套有螺母,螺母上固定有一个力传感器,力传感器套在左右两个固定的套杆(图中未画出)上,弹簧的一端挂在力传感器下端挂钩上,另一端与铁架台底座的固定点相连。当角度传感器顶端转盘带动“T”形螺杆转动时,力传感器会随着“T”形螺杆旋转而上下平移,弹簧长度也随之发生变化。
(1)已知“T”形螺杆的螺纹间距d=4.0×10-3 m,当其旋转300°时,力传感器在竖直方向移动
m。(结果保留2位有效数字)
(2)该探究小组操作步骤如下:
①旋转“T”形螺杆使初状态弹簧长度大于原长。
②记录初状态力传感器示数F0以及角度传感器示数θ0。
③旋转“T”形螺杆使弹簧长度增加,待稳定后,记录力传感器示数F1,其增加量
ΔF1=F1-F0;角度传感器示数θ1,其增加量Δθ1=θ1-θ0。
④多次旋转“T”形螺杆,重复步骤③的操作,在表格中记录多组ΔF、Δθ值,图乙中已描出5个点,请将剩余点在图中描出并连线。
⑤用ΔF、Δθ、d三个量计算弹簧劲度系数k的表达式为k= ;结合图线算出弹簧的劲度系数k= N/m。(结果保留2位有效数字)
专项2 动态平衡问题
题型1 图解法(平行四边形、矢量三角形)
1.(多选)如图所示,在粗糙水平地面上放着一个截面为四分之一圆弧的柱状物体A,A的左端紧靠竖直墙,A与竖直墙之间放一光滑圆球B,已知A的圆半径为球B的半径的3倍,球B所受的重力为G,整个装置处于静止状态。设墙壁对B的弹力为F1,A对B的弹力为F2。若把A向右移动少许后,它们仍处于静止状态,则F1、F2的变化情况分别是( )
A.F1减小 B.F1增大
C.F2增大 D.F2减小
2.[2022福建省泉州市期末考试]如图,光滑小球卡在固定斜面和竖直挡板之间。设球对斜面的弹力为N1,对挡板的弹力为N2。现将挡板绕O点沿逆时针缓慢转到水平位置,在此过程中( )
A.N1始终减小,N2始终增大
B.N1始终增大,N2始终减小
C.N1始终减小,N2先减小再增大
D.N1先减小再增大,N2始终减小
题型2 解析法
3.[2022福建省福州市福建师大附中期末考试]如图所示,光滑半球形容器固定在水平面上,O为球心,一质量为m的小滑块在水平力F的作用下从半球形容器最低点缓慢移近最高点,设滑块所受支持力为FN,滑块可视为质点,则下列判断正确的是( )
A.F缓慢增大,FN缓慢增大
B.F缓慢增大,FN缓慢减小
C.F缓慢减小,FN缓慢增大
D.F缓慢减小,FN缓慢减小
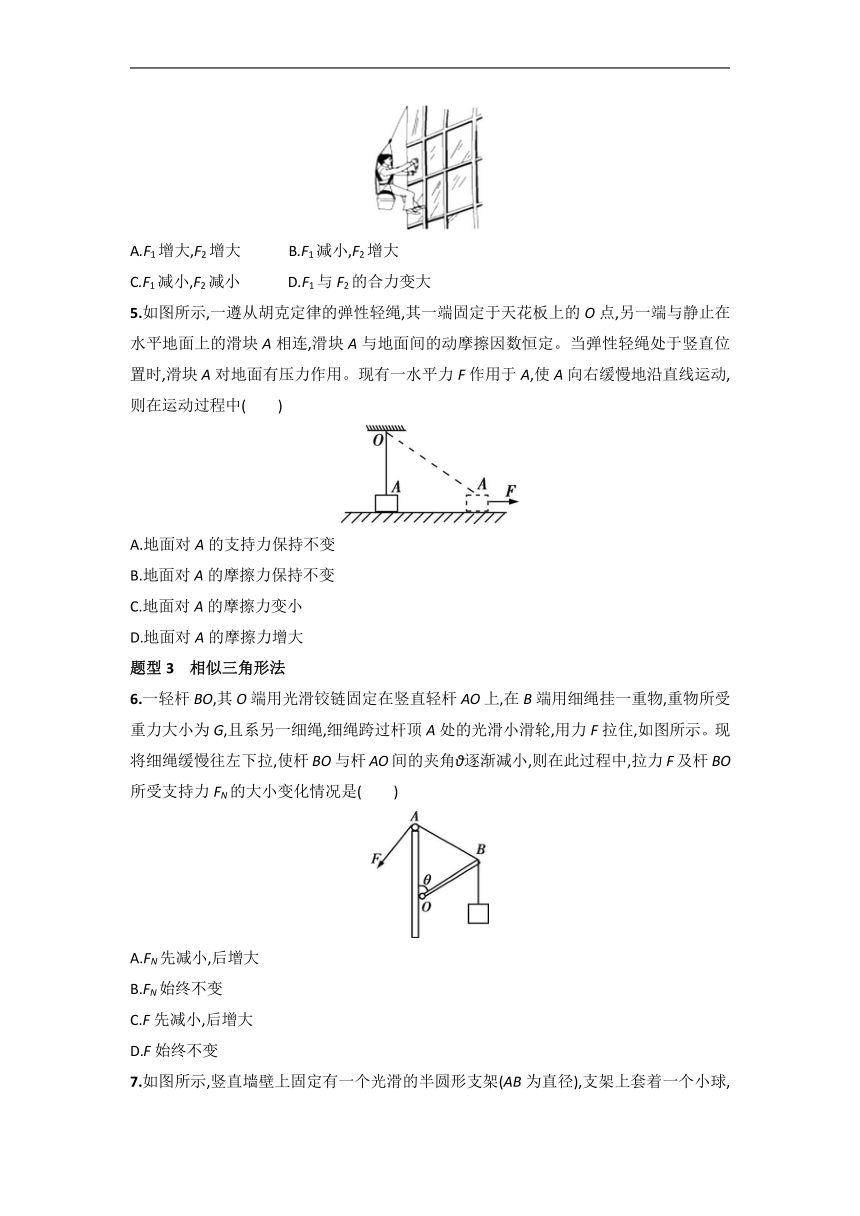
4.[2022广东汕头金山中学期末考试]如图所示,清洗楼房光滑玻璃的工人常用一根绳索将自己悬在空中。若工人及其装备总重力为mg,悬绳与竖直墙壁的夹角为θ,悬绳对工人的拉力为F1,墙壁对工人的弹力为F2,若工人缓慢下移,增加悬绳的长度,则( )
A.F1增大,F2增大 B.F1减小,F2增大
C.F1减小,F2减小 D.F1与F2的合力变大
5.如图所示,一遵从胡克定律的弹性轻绳,其一端固定于天花板上的O点,另一端与静止在水平地面上的滑块A相连,滑块A与地面间的动摩擦因数恒定。当弹性轻绳处于竖直位置时,滑块A对地面有压力作用。现有一水平力F作用于A,使A向右缓慢地沿直线运动,则在运动过程中( )
A.地面对A的支持力保持不变
B.地面对A的摩擦力保持不变
C.地面对A的摩擦力变小
D.地面对A的摩擦力增大
题型3 相似三角形法
6.一轻杆BO,其O端用光滑铰链固定在竖直轻杆AO上,在B端用细绳挂一重物,重物所受重力大小为G,且系另一细绳,细绳跨过杆顶A处的光滑小滑轮,用力F拉住,如图所示。现将细绳缓慢往左下拉,使杆BO与杆AO间的夹角θ逐渐减小,则在此过程中,拉力F及杆BO所受支持力FN的大小变化情况是( )
A.FN先减小,后增大
B.FN始终不变
C.F先减小,后增大
D.F始终不变
7.如图所示,竖直墙壁上固定有一个光滑的半圆形支架(AB为直径),支架上套着一个小球,轻绳的一端悬于P点,另一端与小球相连。已知半圆形支架的半径为R,轻绳长度为L,且RA.F1和F2均增大
B.F1保持不变,F2先增大后减小
C.F1先减小后增大,F2保持不变
D.F1先增大后减小,F2先减小后增大
题型4 辅助圆法
8.(多选)如图所示,置于地面的矩形框架中用两细绳拴住质量为m的小球,绳B水平。设绳A、B对球的拉力大小分别为F1、F2,它们的合力大小为F。现将框架在竖直平面内绕左下端缓慢旋转90°,在此过程中( )
A.F先增大后减小
B.F大小不变
C.F1先增大后减小
D.F2先增大后减小
9.(多选)如图所示,将两块光滑平板OA、OB固定连接,构成顶角为60°的楔形槽,楔形槽内放置一重为G的光滑小球,整个装置保持静止,OA板与水平面夹角为15°。现使楔形槽绕O点顺时针缓慢转动至OA板竖直,则转动过程中( )
A.OA板对小球的作用力NA一直在减小
B.OB板对小球的作用力NB一直在增大
C.OA板对小球的作用力NA的最大值为G
D.OB板对小球的作用力NB大小为G时,OA板对小球的作用力大小也为G
题型5 正弦定理法(或拉密定理)
10.如图所示,a、b两细绳一端系着重力为G的小球,另一端系在竖直放置的圆环上,小球位于圆环的中心,开始时绳a水平,绳b倾斜,现将圆环在竖直平面内顺时针缓慢地向右滚动至绳b水平,在此过程中( )
A.a上的张力逐渐增大,b上的张力逐渐增大
B.a上的张力逐渐减小,b上的张力逐渐减小
C.a上的张力逐渐减小,b上的张力逐渐增大
D.a上的张力逐渐增大,b上的张力逐渐减小
参考答案
专项1 关于胡克定律的实验
1.答案 (1)竖直 (2)静止 L3 1 mm (3)Lx (4)4.9 10
解析 (1)弹簧的轴线必须沿重力方向,所以应沿竖直方向。(2)由于表中测量值已经估读到0.1 mm,所以刻度尺的最小刻度应是1 mm。(3)因为m0g=k(Lx-L0),nmg+m0g=k(Ln-L0),整理得nmg=k(Ln-Lx),所以横轴应为弹簧长度与Lx的差值。(4)k==4.9 N/m,m0==1.0×10-2 kg=10 g。
2.答案 (3)①正比 ②98
解析 (3)①对物块B受力分析,根据平衡条件有F弹+m0g=F,由题图2可得,F=-kx+F0,联立得F弹=-kx+F0-m0g,设不悬挂物块C时弹簧的压缩量为x0,则挂钩相对O点下移x0时,弹簧回到原长,此时有0=-kx0+F0-m0g,即F0-m0g=kx0,即F弹=k(x0-x),x0-x为弹簧形变量,则可认为弹簧的弹力与弹簧的形变量成正比。
②由①中解析可知,F-x图像斜率的绝对值表示弹簧的劲度系数,则k= N/m=98 N/m。
3.答案
解析 设每个钩码所受浮力为F,由题意可列关系式k(xn-x0)=4mg-nF,则xn=-n++x0,解得k=,F=。
4.答案 (1)3.3×10-3 (2)④如图所示
⑤ 23(22也可)
解析 (1)当“T”形螺杆旋转360°时,力传感器在竖直方向上移动d=4.0×10-3 m,则当“T”形螺杆旋转300°时,力传感器在竖直方向移动的距离为x= m=×10-3 m≈3.3×10-3 m。(2)④描点作图如答图所示。⑤角度增加Δθ时,弹簧长度的变化量为Δx,则有Δx=,根据胡克定律得ΔF=kΔx,解得k=,变形得ΔF=Δθ,图线的斜率为,解得k≈23 N/m。
专项2 动态平衡问题
1.AD 解析法:以球B为研究对象,受力分析如图甲所示,根据合成法,可得出F1=Gtan θ,F2=,当A向右移动少许后,θ减小,则F1减小,F2减小,选项AD正确。
图解法:先根据平衡条件和平行四边形定则画出如图乙所示的矢量三角形,在θ减小的过程中,从图乙中可直观地看出,F1减小,F2减小,选项AD正确。
2.C 对球受力分析如图,将N'1与N'2合成,其合力与重力等大反向,挡板转动时,挡板给球的弹力N'2与斜面给球的弹力N'1的合力大小、方向均不变,其中N'1的方向不变,N'2的方向按图中a、b、c的规律变化,则N'2的大小先变小后变大,其中挡板与斜面垂直时最小;与此对应,N'1的大小一直减小;又N'2=N2,N'1=N1,则N1始终减小,N2先减小再增大,只有C正确。
3.A 对物体进行受力分析如图所示,物体受重力G、支持力FN、水平力F,小滑块从半球形容器最低点缓慢移近最高点的过程中,我们可以看成小滑块每一个状态都是平衡状态,根据平衡条件,应用力的合成得出F=,FN=,由于小滑块从半球形容器最低点缓慢移近最高点,所以θ减小,tan θ减小,sin θ减小。根据以上表达式可知F增大,FN增大,选项A正确。
4.C 工人受到重力、弹力和拉力,如图,根据共点力平衡条件,有F1=,F2=mgtan θ,当工人下移时,悬绳与竖直方向的夹角θ变小,故F1变小,F2变小,但F1 与F2的合力与重力平衡,大小不变,故C正确,ABD错误。
5.C 弹性轻绳处于竖直方向时,设其伸长量为x1,劲度系数为k,则受力分析如图甲所示。根据平衡条件得T1+N1=G,T1=kx1。向右拉至某一位置时,受力如图乙所示,其中θ为此时弹性轻绳与水平面的夹角,根据正交分解和力的平衡条件可得T2sin θ+N2=G, T2cos θ+f=F,T2=kx2。设弹性轻绳自然长度为l,则l+x1=(l+x2)sin θ,所以有N2=G-kx2sin θ=G-k(l+x1-lsin θ),f=F-T2cos θ,可知随着A向右缓慢移动,θ减小,地面对A的支持力减小,A与地面间的摩擦力变小。所以C正确。
6.B 取BO杆的B端为研究对象,受到绳子拉力(大小为F)、支持力FN和悬挂重物的绳子的拉力(大小为G)的作用,将FN与G合成,其合力与F等值反向,如图所示,B端所受的三个力构成矢量三角形(图中阴影部分),力的三角形与几何三角形OBA相似,利用相似三角形对应边成比例可得,式中G、H、L均不变,l逐渐变小,可知FN不变,F逐渐变小,选项B正确。
7.A 对小球受力分析如图所示,因为几何三角形与力三角形相似,所以有,将轻绳的上端点P沿墙壁缓慢下移至A点的过程,OP减小,所以F1和F2均增大,选项A正确。
8.BD 对小球受力分析,小球处于静止状态,受力平衡,两绳的拉力的合力与小球重力大小相等、方向相反,则F不变,B正确,A错误;两绳拉力夹角不变,构建一个圆,如图所示,将框架在竖直平面内绕左下端缓慢旋转90°的过程中,F1逐渐减小,F2先增大后减小,当绳A处于水平方向时,F2最大,故D正确,C错误。
9.BCD 取小球为研究对象,受到OA板、OB板的弹力和重力G,三力构成矢量三角形(如图甲所示的实线三角形DEH),重力G大小、方向不变,∠DEH=60°,恒定不变。当EH⊥DH时,NA、NB的大小关系可以从以实线DE为直径的圆中找。在转动过程中弦DH恒定不变,如图甲所示,OB板从开始位置转动到竖直位置,即E从位置1到位置2的过程,NA、NB都在增大;OB板从竖直位置继续转动至OA板竖直,即E从位置2到位置4的过程,NA在减小,NB在增大,故整个过程OA板对小球的作用力先增大后减小,而OB板对小球的作用力一直在增大,故选项A错误,B正确。当OB板在竖直位置时,OA板对小球的作用力有最大值,此时对小球受力分析,如图乙所示,根据平衡条件得NA=G,故选项C正确。当OC线竖直时,球处于静止状态,受力平衡,根据几何关系可知,两平板对球的弹力大小相等,且夹角为120°,根据平衡条件得NA=NB=G,故选项D正确。
10.D 设圆环沿顺时针方向滚动过程中b绳与竖直方向的夹角为θ,a绳和b绳的拉力大小分别为T1、T2,小球的位置相对圆环保持不动,小球受力保持平衡,由平衡条件可知,两绳拉力的合力不变,小球受到的重力G和T1、T2组成一个闭合的矢量三角形,如图所示,由几何知识可知T1、T2的夹角π-β不变,由正弦定理可得,在-β≤θ≤范围内,θ变大,T1变大,T2变小,选项D正确。
专项1 关于胡克定律的实验
1.某同学探究弹簧弹力与形变量的关系。
(1)将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧。弹簧轴线和刻度尺都应在 方向上(填“水平”或“竖直”)。
(2)弹簧自然悬挂,待弹簧 时,长度记为L0;弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10 g砝码,弹簧长度依次记为L1至L6,数据如下表:
代表符号 L0 Lx L1 L2 L3 L4 L5 L6
数值(cm) 25.35 27.35 29.35 31.30 33.4 35.35 37.40 39.30
表中有一个数值记录不规范,代表符号为 。由表可知所用刻度尺的最小分度为 。
(3)如图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与 的差值(填“L0”或“Lx”)。
(4)由图可知弹簧的劲度系数为 N/m;通过图和表可知砝码盘的质量为 g(结果保留2位有效数字,重力加速度取9.8 m/s2)。
2.[2022海南中学期中考试]某同学利用图1所示装置来研究弹簧弹力与形变量的关系。设计的实验如下:A、B是质量均为m0的小物块,A、B间由轻弹簧相连,A的上面通过轻绳绕过两个定滑轮与一个轻质挂钩相连。挂钩上可以挂上不同质量的物块C。物块B下方放置一压力传感器。物块C右边有一个竖直的直尺,可以测出挂钩下移的距离。整个实验中弹簧均处于弹性限度内,重力加速度g=9.8 m/s2。实验操作如下:
(1)不悬挂物块C,让系统保持静止,确定挂钩的位置O,并读出压力传感器的示数F0。
(2)每次挂上不同质量的物块C,用手托住,缓慢释放。测出系统稳定时挂钩相对O点下移的距离xi,并读出相应的压力传感器的示数Fi。
(3)以压力传感器示数为纵坐标,挂钩下移距离为横坐标,根据每次测量的数据,描点作出F-x图像如图2所示。
①由图像可知,在实验误差允许的范围内,可以认为弹簧弹力与弹簧形变量成 (选填“正比”“反比”或“不确定关系”);
②由图像可知,弹簧劲度系数k= N/m。
3.[2022北京市十一学校期末考试]某同学在“探究弹力和弹簧伸长量的关系”时的实验装置如图所示,让刻度尺零刻度与弹簧上端齐平,弹簧不挂物体时下端指针所指的刻度为x0,在弹簧下用足够长的轻质细线挂上4个相同的钩码(弹簧处于弹性限度内),静止置于烧杯T内,控制阀门S通过细胶管向烧杯中缓慢注水,依次浸没4个钩码,记录每浸没一个钩码时指针所指的刻度分别为x1、x2、x3、x4,已知每个钩码的质量均为m,重力加速度为g,以xn为纵坐标,n为横坐标建立坐标系,作出xn和浸没钩码个数n的关系图像,求得图像斜率为a,纵截距为b,则该弹簧的劲度系数为 ,每个钩码所受浮力为 。(用a、b、m、g和x0表示)
4.[2021八省八校联考]2020年12月8日,中尼两国共同宣布了珠穆朗玛峰的最新高度为海拔8 848.86米,此次珠峰高度测量实现了北斗卫星导航系统首次应用、首次实测珠峰峰顶重力值等多项第一。同时,雪深探测雷达、重力仪、超长距离测距仪等一大批国产现代测量设备纷纷亮相。重力仪的内部包含了由弹簧组成的静力平衡系统。为测量某弹簧的劲度系数,某探究小组设计了如下实验。实验装置如图甲所示,角度传感器与可转动“T”形螺杆相连,“T”形螺杆上套有螺母,螺母上固定有一个力传感器,力传感器套在左右两个固定的套杆(图中未画出)上,弹簧的一端挂在力传感器下端挂钩上,另一端与铁架台底座的固定点相连。当角度传感器顶端转盘带动“T”形螺杆转动时,力传感器会随着“T”形螺杆旋转而上下平移,弹簧长度也随之发生变化。
(1)已知“T”形螺杆的螺纹间距d=4.0×10-3 m,当其旋转300°时,力传感器在竖直方向移动
m。(结果保留2位有效数字)
(2)该探究小组操作步骤如下:
①旋转“T”形螺杆使初状态弹簧长度大于原长。
②记录初状态力传感器示数F0以及角度传感器示数θ0。
③旋转“T”形螺杆使弹簧长度增加,待稳定后,记录力传感器示数F1,其增加量
ΔF1=F1-F0;角度传感器示数θ1,其增加量Δθ1=θ1-θ0。
④多次旋转“T”形螺杆,重复步骤③的操作,在表格中记录多组ΔF、Δθ值,图乙中已描出5个点,请将剩余点在图中描出并连线。
⑤用ΔF、Δθ、d三个量计算弹簧劲度系数k的表达式为k= ;结合图线算出弹簧的劲度系数k= N/m。(结果保留2位有效数字)
专项2 动态平衡问题
题型1 图解法(平行四边形、矢量三角形)
1.(多选)如图所示,在粗糙水平地面上放着一个截面为四分之一圆弧的柱状物体A,A的左端紧靠竖直墙,A与竖直墙之间放一光滑圆球B,已知A的圆半径为球B的半径的3倍,球B所受的重力为G,整个装置处于静止状态。设墙壁对B的弹力为F1,A对B的弹力为F2。若把A向右移动少许后,它们仍处于静止状态,则F1、F2的变化情况分别是( )
A.F1减小 B.F1增大
C.F2增大 D.F2减小
2.[2022福建省泉州市期末考试]如图,光滑小球卡在固定斜面和竖直挡板之间。设球对斜面的弹力为N1,对挡板的弹力为N2。现将挡板绕O点沿逆时针缓慢转到水平位置,在此过程中( )
A.N1始终减小,N2始终增大
B.N1始终增大,N2始终减小
C.N1始终减小,N2先减小再增大
D.N1先减小再增大,N2始终减小
题型2 解析法
3.[2022福建省福州市福建师大附中期末考试]如图所示,光滑半球形容器固定在水平面上,O为球心,一质量为m的小滑块在水平力F的作用下从半球形容器最低点缓慢移近最高点,设滑块所受支持力为FN,滑块可视为质点,则下列判断正确的是( )
A.F缓慢增大,FN缓慢增大
B.F缓慢增大,FN缓慢减小
C.F缓慢减小,FN缓慢增大
D.F缓慢减小,FN缓慢减小
4.[2022广东汕头金山中学期末考试]如图所示,清洗楼房光滑玻璃的工人常用一根绳索将自己悬在空中。若工人及其装备总重力为mg,悬绳与竖直墙壁的夹角为θ,悬绳对工人的拉力为F1,墙壁对工人的弹力为F2,若工人缓慢下移,增加悬绳的长度,则( )
A.F1增大,F2增大 B.F1减小,F2增大
C.F1减小,F2减小 D.F1与F2的合力变大
5.如图所示,一遵从胡克定律的弹性轻绳,其一端固定于天花板上的O点,另一端与静止在水平地面上的滑块A相连,滑块A与地面间的动摩擦因数恒定。当弹性轻绳处于竖直位置时,滑块A对地面有压力作用。现有一水平力F作用于A,使A向右缓慢地沿直线运动,则在运动过程中( )
A.地面对A的支持力保持不变
B.地面对A的摩擦力保持不变
C.地面对A的摩擦力变小
D.地面对A的摩擦力增大
题型3 相似三角形法
6.一轻杆BO,其O端用光滑铰链固定在竖直轻杆AO上,在B端用细绳挂一重物,重物所受重力大小为G,且系另一细绳,细绳跨过杆顶A处的光滑小滑轮,用力F拉住,如图所示。现将细绳缓慢往左下拉,使杆BO与杆AO间的夹角θ逐渐减小,则在此过程中,拉力F及杆BO所受支持力FN的大小变化情况是( )
A.FN先减小,后增大
B.FN始终不变
C.F先减小,后增大
D.F始终不变
7.如图所示,竖直墙壁上固定有一个光滑的半圆形支架(AB为直径),支架上套着一个小球,轻绳的一端悬于P点,另一端与小球相连。已知半圆形支架的半径为R,轻绳长度为L,且R
B.F1保持不变,F2先增大后减小
C.F1先减小后增大,F2保持不变
D.F1先增大后减小,F2先减小后增大
题型4 辅助圆法
8.(多选)如图所示,置于地面的矩形框架中用两细绳拴住质量为m的小球,绳B水平。设绳A、B对球的拉力大小分别为F1、F2,它们的合力大小为F。现将框架在竖直平面内绕左下端缓慢旋转90°,在此过程中( )
A.F先增大后减小
B.F大小不变
C.F1先增大后减小
D.F2先增大后减小
9.(多选)如图所示,将两块光滑平板OA、OB固定连接,构成顶角为60°的楔形槽,楔形槽内放置一重为G的光滑小球,整个装置保持静止,OA板与水平面夹角为15°。现使楔形槽绕O点顺时针缓慢转动至OA板竖直,则转动过程中( )
A.OA板对小球的作用力NA一直在减小
B.OB板对小球的作用力NB一直在增大
C.OA板对小球的作用力NA的最大值为G
D.OB板对小球的作用力NB大小为G时,OA板对小球的作用力大小也为G
题型5 正弦定理法(或拉密定理)
10.如图所示,a、b两细绳一端系着重力为G的小球,另一端系在竖直放置的圆环上,小球位于圆环的中心,开始时绳a水平,绳b倾斜,现将圆环在竖直平面内顺时针缓慢地向右滚动至绳b水平,在此过程中( )
A.a上的张力逐渐增大,b上的张力逐渐增大
B.a上的张力逐渐减小,b上的张力逐渐减小
C.a上的张力逐渐减小,b上的张力逐渐增大
D.a上的张力逐渐增大,b上的张力逐渐减小
参考答案
专项1 关于胡克定律的实验
1.答案 (1)竖直 (2)静止 L3 1 mm (3)Lx (4)4.9 10
解析 (1)弹簧的轴线必须沿重力方向,所以应沿竖直方向。(2)由于表中测量值已经估读到0.1 mm,所以刻度尺的最小刻度应是1 mm。(3)因为m0g=k(Lx-L0),nmg+m0g=k(Ln-L0),整理得nmg=k(Ln-Lx),所以横轴应为弹簧长度与Lx的差值。(4)k==4.9 N/m,m0==1.0×10-2 kg=10 g。
2.答案 (3)①正比 ②98
解析 (3)①对物块B受力分析,根据平衡条件有F弹+m0g=F,由题图2可得,F=-kx+F0,联立得F弹=-kx+F0-m0g,设不悬挂物块C时弹簧的压缩量为x0,则挂钩相对O点下移x0时,弹簧回到原长,此时有0=-kx0+F0-m0g,即F0-m0g=kx0,即F弹=k(x0-x),x0-x为弹簧形变量,则可认为弹簧的弹力与弹簧的形变量成正比。
②由①中解析可知,F-x图像斜率的绝对值表示弹簧的劲度系数,则k= N/m=98 N/m。
3.答案
解析 设每个钩码所受浮力为F,由题意可列关系式k(xn-x0)=4mg-nF,则xn=-n++x0,解得k=,F=。
4.答案 (1)3.3×10-3 (2)④如图所示
⑤ 23(22也可)
解析 (1)当“T”形螺杆旋转360°时,力传感器在竖直方向上移动d=4.0×10-3 m,则当“T”形螺杆旋转300°时,力传感器在竖直方向移动的距离为x= m=×10-3 m≈3.3×10-3 m。(2)④描点作图如答图所示。⑤角度增加Δθ时,弹簧长度的变化量为Δx,则有Δx=,根据胡克定律得ΔF=kΔx,解得k=,变形得ΔF=Δθ,图线的斜率为,解得k≈23 N/m。
专项2 动态平衡问题
1.AD 解析法:以球B为研究对象,受力分析如图甲所示,根据合成法,可得出F1=Gtan θ,F2=,当A向右移动少许后,θ减小,则F1减小,F2减小,选项AD正确。
图解法:先根据平衡条件和平行四边形定则画出如图乙所示的矢量三角形,在θ减小的过程中,从图乙中可直观地看出,F1减小,F2减小,选项AD正确。
2.C 对球受力分析如图,将N'1与N'2合成,其合力与重力等大反向,挡板转动时,挡板给球的弹力N'2与斜面给球的弹力N'1的合力大小、方向均不变,其中N'1的方向不变,N'2的方向按图中a、b、c的规律变化,则N'2的大小先变小后变大,其中挡板与斜面垂直时最小;与此对应,N'1的大小一直减小;又N'2=N2,N'1=N1,则N1始终减小,N2先减小再增大,只有C正确。
3.A 对物体进行受力分析如图所示,物体受重力G、支持力FN、水平力F,小滑块从半球形容器最低点缓慢移近最高点的过程中,我们可以看成小滑块每一个状态都是平衡状态,根据平衡条件,应用力的合成得出F=,FN=,由于小滑块从半球形容器最低点缓慢移近最高点,所以θ减小,tan θ减小,sin θ减小。根据以上表达式可知F增大,FN增大,选项A正确。
4.C 工人受到重力、弹力和拉力,如图,根据共点力平衡条件,有F1=,F2=mgtan θ,当工人下移时,悬绳与竖直方向的夹角θ变小,故F1变小,F2变小,但F1 与F2的合力与重力平衡,大小不变,故C正确,ABD错误。
5.C 弹性轻绳处于竖直方向时,设其伸长量为x1,劲度系数为k,则受力分析如图甲所示。根据平衡条件得T1+N1=G,T1=kx1。向右拉至某一位置时,受力如图乙所示,其中θ为此时弹性轻绳与水平面的夹角,根据正交分解和力的平衡条件可得T2sin θ+N2=G, T2cos θ+f=F,T2=kx2。设弹性轻绳自然长度为l,则l+x1=(l+x2)sin θ,所以有N2=G-kx2sin θ=G-k(l+x1-lsin θ),f=F-T2cos θ,可知随着A向右缓慢移动,θ减小,地面对A的支持力减小,A与地面间的摩擦力变小。所以C正确。
6.B 取BO杆的B端为研究对象,受到绳子拉力(大小为F)、支持力FN和悬挂重物的绳子的拉力(大小为G)的作用,将FN与G合成,其合力与F等值反向,如图所示,B端所受的三个力构成矢量三角形(图中阴影部分),力的三角形与几何三角形OBA相似,利用相似三角形对应边成比例可得,式中G、H、L均不变,l逐渐变小,可知FN不变,F逐渐变小,选项B正确。
7.A 对小球受力分析如图所示,因为几何三角形与力三角形相似,所以有,将轻绳的上端点P沿墙壁缓慢下移至A点的过程,OP减小,所以F1和F2均增大,选项A正确。
8.BD 对小球受力分析,小球处于静止状态,受力平衡,两绳的拉力的合力与小球重力大小相等、方向相反,则F不变,B正确,A错误;两绳拉力夹角不变,构建一个圆,如图所示,将框架在竖直平面内绕左下端缓慢旋转90°的过程中,F1逐渐减小,F2先增大后减小,当绳A处于水平方向时,F2最大,故D正确,C错误。
9.BCD 取小球为研究对象,受到OA板、OB板的弹力和重力G,三力构成矢量三角形(如图甲所示的实线三角形DEH),重力G大小、方向不变,∠DEH=60°,恒定不变。当EH⊥DH时,NA、NB的大小关系可以从以实线DE为直径的圆中找。在转动过程中弦DH恒定不变,如图甲所示,OB板从开始位置转动到竖直位置,即E从位置1到位置2的过程,NA、NB都在增大;OB板从竖直位置继续转动至OA板竖直,即E从位置2到位置4的过程,NA在减小,NB在增大,故整个过程OA板对小球的作用力先增大后减小,而OB板对小球的作用力一直在增大,故选项A错误,B正确。当OB板在竖直位置时,OA板对小球的作用力有最大值,此时对小球受力分析,如图乙所示,根据平衡条件得NA=G,故选项C正确。当OC线竖直时,球处于静止状态,受力平衡,根据几何关系可知,两平板对球的弹力大小相等,且夹角为120°,根据平衡条件得NA=NB=G,故选项D正确。
10.D 设圆环沿顺时针方向滚动过程中b绳与竖直方向的夹角为θ,a绳和b绳的拉力大小分别为T1、T2,小球的位置相对圆环保持不动,小球受力保持平衡,由平衡条件可知,两绳拉力的合力不变,小球受到的重力G和T1、T2组成一个闭合的矢量三角形,如图所示,由几何知识可知T1、T2的夹角π-β不变,由正弦定理可得,在-β≤θ≤范围内,θ变大,T1变大,T2变小,选项D正确。
