第三单元长方形和正方形易错题检测卷(单元测试)-小学数学三年级上册苏教版(含解析)
文档属性
| 名称 | 第三单元长方形和正方形易错题检测卷(单元测试)-小学数学三年级上册苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 911.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三单元长方形和正方形易错题检测卷(单元测试)-小学数学三年级上册苏教版
一、选择题
1.把一个长为8厘米,宽为6厘米的长方形平均剪成两个长方形,周长比原来增加了( )厘米。
A.16 B.12 C.16或12
2.用两个边长4米的正方形拼成一个长方形,拼成的长方形周长是( )。
A.16米 B.24米 C.32米
3.学校篮球场长140米,宽20米,沿篮球场军官跑两圈是( )米。
A.200 B.320 C.640
4.下图中,甲乙两图形的周长相比,( )。
A.甲的周长长 B.乙的周长长 C.一样长
5.从一个长12厘米,宽9厘米的长方形纸片上剪下一个最大的正方形,正方形的边长是( )。
A.12厘米 B.3厘米 C.9厘米
6.在一张长18cm、宽10cm的长方形纸板上剪边长为3cm的小正方形,最多能剪( )个。
A.10 B.18 C.20
7.下图是分别用4个同样大小的正方形拼成的,周长最小的是( )。
A. B. C.
8.一个长方形的周长是24厘米,它的长和宽可能是( )。
A.8厘米和4厘米 B.8厘米和3厘米 C.6厘米和3厘米
二、填空题
9.用4个边长2厘米的小正方形拼成一个长方形或正方形,拼成的图形的周长可能是( )厘米,也可能是( )厘米。
10.小红用一根长120厘米的铁丝正好围成一个正方形,她围成的正方形的边长是( )厘米。如果这个正方形的每条边的长度都增加5厘米,那么这根铁丝的长度应增加( )厘米。
11.如图,一个长是15厘米,宽是10厘米的大长方形被分成了3个同样大的小长方形,小长方形的宽是( )厘米,周长是( )厘米。
12.一个长方形的长增加5厘米,宽增加3厘米,它的周长增加( )厘米。
13.一个长方形的周长是32厘米,宽是6厘米,长是( )厘米。
14.长方形游泳池长50米,宽30米,乐乐绕着游泳池走一圈,他走了( )米。
15.把一个长8厘米、宽4厘米的长方形,分成两个完全一样的小正方形,每个小正方形的周长是( )厘米;如果用4个边长是5厘米的小正方形,拼成一个大正方形,拼成的大正方形的周长是( )厘米。
16.两个长5厘米,宽2厘米的长方形拼成下面的图形,这个图形的周长是( )厘米。
三、判断题
17.一个长方形和一个正方形的周长相等,长方形的长是10厘米,宽是6厘米,那么正方形的边长是9厘米。( )
18.周长相等的两个长方形,它们各边的长也一定相同。( )
19.如左图,将一张长方形纸沿虚线对折,可以验证长方形的两条短边相等。( )
20.一个长方形菜地长55米,宽45米。妈妈沿着菜地跑一圈,跑了100米。( )
21.正方形的周长是4厘米,两个这样的正方形拼成的长方形周长是8厘米。( )
四、图形计算
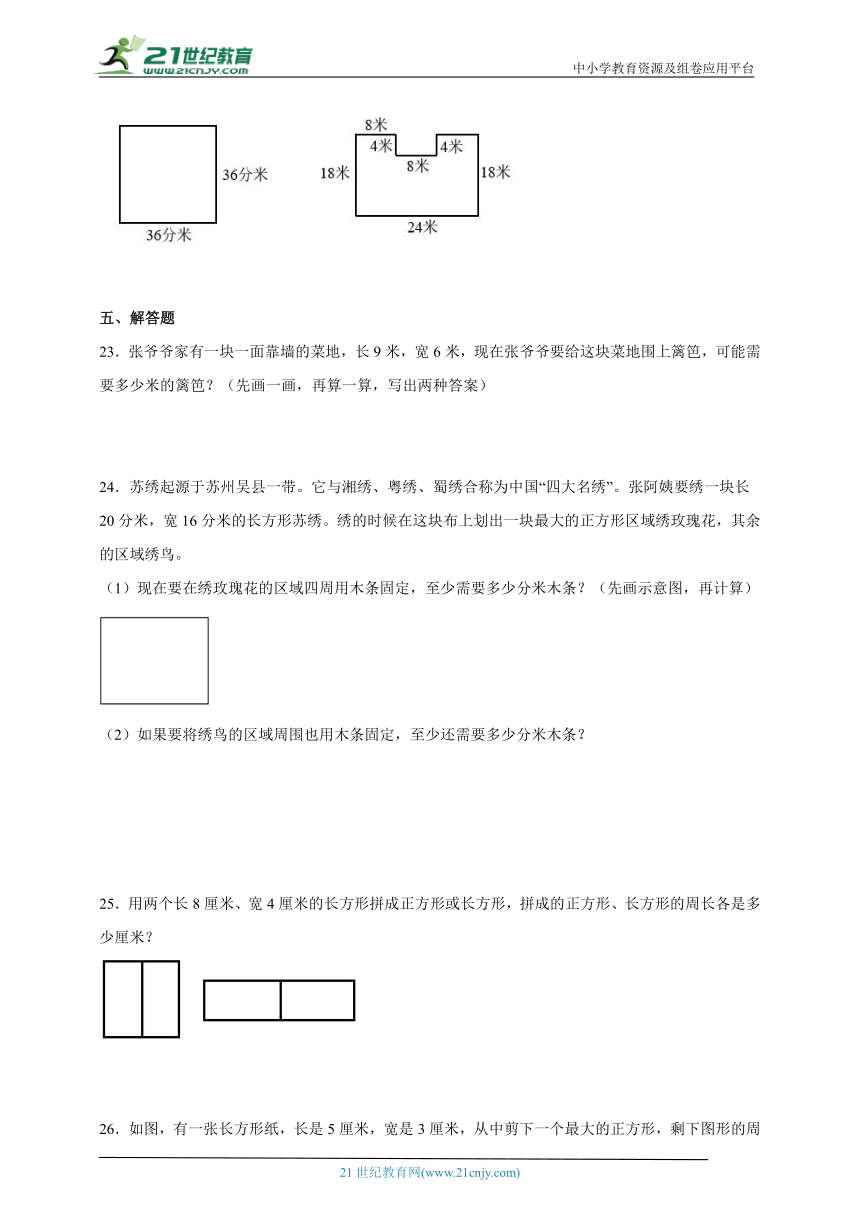
22.计算下面各图形的周长。
五、解答题
23.张爷爷家有一块一面靠墙的菜地,长9米,宽6米,现在张爷爷要给这块菜地围上篱笆,可能需要多少米的篱笆?(先画一画,再算一算,写出两种答案)
24.苏绣起源于苏州吴县一带。它与湘绣、粤绣、蜀绣合称为中国“四大名绣”。张阿姨要绣一块长20分米,宽16分米的长方形苏绣。绣的时候在这块布上划出一块最大的正方形区域绣玫瑰花,其余的区域绣鸟。
(1)现在要在绣玫瑰花的区域四周用木条固定,至少需要多少分米木条?(先画示意图,再计算)
(2)如果要将绣鸟的区域周围也用木条固定,至少还需要多少分米木条?
25.用两个长8厘米、宽4厘米的长方形拼成正方形或长方形,拼成的正方形、长方形的周长各是多少厘米?
26.如图,有一张长方形纸,长是5厘米,宽是3厘米,从中剪下一个最大的正方形,剩下图形的周长是多少厘米?(先画一画,再算一算)
27.小兰有一张长26厘米,宽6厘米的长方形彩纸,她想从上面剪下2个相连的最大的正方形做手工,剪下图形的周长是多少厘米?剩下的彩纸还能剪几个最大的正方形?建议:先画一画,再算一算。
28.小明用一根铁丝做了一个长18厘米,宽10厘米的长方形框架,这个框架的周长是多少厘米?如果小明把它改围成正方形,这个正方形的边长是多少厘米?
参考答案:
1.C
【分析】如下图,横着剪成两个长方形,周长增加两个长的长度,即8×2=16(厘米),如果竖着剪成两个长方形,周长增加2个宽的长度,即6×2=12(厘米),据此即可解答。
【详解】根据分析可知,把一个长为8厘米,宽为6厘米的长方形平均剪成两个长方形,周长比原来增加了16或12厘米。
故答案为:C。
【点睛】把一个长方形平均剪成两个长方形可以横着剪,也可以竖着剪,两种剪法得到的长方形不一样。
2.B
【分析】用2个边长4米的小正方形拼成一个长方形,方法只有一种,摆成后的长方形的长是(4+4)米,宽是4米,长方形周长=(长+宽)×2,带入数据求解。
【详解】(4+4+4)×2
=12×2
=24(米)
故答案为:B
【点睛】本题的关键是求出拼成后长方形的长和宽,再根据长方形的周长公式进行计算。
3.C
【分析】篮球场的长加宽的和乘2等于篮球场的周长,再乘跑的圈数即可解答。
【详解】(140+20)×2×2
=160×4
=640(米)
故答案为:C。
【点睛】熟练掌握长方形的周长公式是解答本题的关键。
4.C
【分析】通过观察上图可知,长方形的对边相等,中间曲线段是甲乙两图形的公共边,所以甲乙两图形的周长相等。
【详解】根据分析可知,甲乙两图形的周长相等。
故答案为:C。
【点睛】本题主要考查学生的观察和分析问题的能力。
5.C
【详解】略
6.B
【分析】先用长除以3,再用宽除以3,然后把商相乘即可解答。
【详解】18÷3=6(个)
10÷3=3(个)……1(厘米)
6×3=18(个)
故答案为:B。
【点睛】先看长能剪几个3厘米的线段,宽能剪几个3厘米的线段,再作进一步解答。
7.C
【分析】分别计算出各图形的周长即可解答。
【详解】A.(4+1)×2=5×2=10
B.(3+1)×2+4=4×2+4=12
C.2×4=8
12>10>8,第3个图形的周长最小。
故答案为:C。
【点睛】本题主要考查学生对周长的认识。
8.A
【分析】根据长方形的周长=(长+宽)×2,所以:长+宽=长方形的周长÷2,即24÷2=12,然后将A、B、C三项各自的长和宽进行相加,等于12厘米的即可。
【详解】A.8+4=12(厘米);
B.8+3=11(厘米);
C.6+3=9(厘米)
故答案为:A
【点睛】本题考查了长方形的周长公式的掌握和灵活运用。
.
9. 20 16
【分析】根据题意:4个边长2厘米的正方形可以拼成一个长方形或正方形,长方形的周长:(长+宽)×2,带入即可,也可以拼成一个正方形,正方形的周长:边长×4,带入即可解答。
【详解】拼成一个长方形的周长是:
(8+2)×2
=10×2
=20(厘米);
拼成一个正方形的周长是:
(2+2)×4
=4×4
=16(厘米)
【点睛】根据题意进行拼组,然后根据长方形和正方形的周长计算公式,进行计算即可解答。
10. 30 20
【分析】根据题意可知,铁丝长度等于正方形的周长。根据正方形的边长=周长÷4,求出正方形的边长。根据正方形的周长=边长×4可知,每条边的长度都增加5厘米,周长增加4个5厘米。
【详解】120÷4=30(厘米)
则她围成的正方形的边长是30厘米。
5×4=20(厘米)
则这根铁丝的长度应增加20厘米。
【点睛】本题考查正方形周长公式的灵活运用。正方形的周长=边长×4,正方形的边长=周长÷4。
11. 5 30
【分析】观察图形可知:小长方形的长=大长方形的宽;小长方形的长=小长方形的两个宽;据此求出小长方形的长和宽,即可进行解答。
【详解】小长方形的宽:10÷2=5(厘米);
周长:(10+5)×2
=15×2
=30(厘米)
【点睛】观察图形求得小长方形的宽是解题关键。
12.16
【分析】根据长方形的可知,长方形有两个长和两个宽,则长增加5厘米,两个长久增加5×2=10厘米,宽增加3厘米,则两个宽就增加3×2=6厘米,即可求得周长增加的厘米数。
【详解】5×2=10(厘米);
3×2=6(厘米)
10+6=16(厘米)
【点睛】此题主要考查长方形的周长的灵活运用。
13.10
【分析】长方形的周长除以2,再减去宽的长度,等于长方形的长。
【详解】32÷2-6
=16-6
=10(厘米)
【点睛】熟练运用长方形的周长公式是解答本题的关键。
14.160
【分析】绕着游泳池走一圈即求长方形游泳池的周长,根据长方形的周长=(长+宽)×2,计算即可解答。
【详解】(50+30)×2
=80×2
=160(米)
【点睛】本题看出了长方形的周长的理解和灵活运用。
15. 16 40
【分析】根据题意,长方形的长8厘米刚好可以分成2个正方形的边长8÷2=4厘米,长方形的宽4厘米,为正方形另一边的边长,根据正方形的周长公式=边长×4,计算即可;
如果用4个边长5厘米的小正方形,拼成一个大正方形,大正方形的边长是2个小正方形的边长,即5×2=10厘米,根据正方形的周长公式,计算即可解答。
【详解】小正方的边长是4厘米;
小正方形的周长:4×4=16厘米;
大正方形的边长:5×2=10(厘米)
大正方形的周长:10×4=40(厘米)。
【点睛】本题的关键是明确正方形的边长是多少,并熟记正方形的周长公式。
16.24
【分析】根据题图可知,图形的周长比两个长方形的周长和少2个宽。根据长方形的周长=(长+宽)×2,求出长方形的周长。再乘2,求出2个长方形的周长和。再减去2个宽,即可求出图形的周长。
【详解】(5+2)×2×2-2×2
=7×2×2-2×2
=28-4
=24(厘米)
则这个图形的周长是24厘米。
【点睛】熟练掌握长方形的周长公式,灵活运用公式解决问题。
17.×
【分析】根据长方形的周长=(长+宽)×2,把数据代入公式求出长方形的周长,再根据正方形的边长=周长÷4,求出正方形的边长,然后与9厘米进行比较。
【详解】(10+6)×2÷4
=16×2÷4
=32÷4
=8(厘米)
则正方形的边长是8厘米,因此题干中的结论是错误的。
故答案为:×。
【点睛】此题主要考查长方形、正方形周长公式的灵活运用,关键是熟记公式。
18.×
【分析】长方形的周长=(长+宽)×2,当两个长方形的周长相等时,两个长方形的长与宽的和相等,不能确定两个长方形的长相等,宽相等,即两个长方形的形状相同。例如周长为16厘米的两个长方形,一个长5厘米、宽3厘米,另一个长6厘米、宽2厘米。据此判断即可。
【详解】根据分析可知,周长相等的两个长方形,它们各边的长不一定相同,故原题干说法错误。
故答案为:×
【点睛】熟记长方形的周长公式:长方形的周长=(长+宽)×2,长方形的周长大小和长与宽两个量有关。
19.×
【分析】按照如图方式对折,可以发现长方形的两条长边重合,可以验证长方形的两条长边相等。
【详解】按照图中的折叠方式,并不能验证长方形的两条短边相等;
题干阐述错误,故答案为:×。
【点睛】长方形的对边相等且互相平行,当长方形的一组邻边也相等时,将会变成正方形。
20.×
【分析】根据长方形的周长=(长+宽)×2即可求得菜地的周长,再与妈妈跑的路程比较即可解答。
【详解】(55+45)×2
=100×2
=200(米)
200米>100米;
故答案为:×
【点睛】掌握长方形的周长公式是解题的关键。
21.×
【分析】两个正方形拼成一个长方形,则长方形的长等于2个正方形的边长,宽等于正方形的边长。根据正方形的边长=周长÷4,求出正方形的边长。再根据长方形的周长=(长+宽)×2解答。
【详解】4÷4=1(厘米)
(2×1+1)×2
=3×2
=6(厘米)
则长方形的周长是6厘米。
所以原题说法错误。
故答案为:×
【点睛】本题关键是明确长方形的长与宽,再根据正方形和长方形的周长公式解答。
22.144分米;92米
【分析】(1)根据正方形的周长=边长×4,解答即可;
(2)
如图所示,将图形的边向上平移后可知,图形的周长等于长24米宽18米的长方形的周长,再加上两个4米,据此解答即可。
【详解】36×4=144(分米)
正方形的周长是144分米。
(24+18)×2+4×2
=42×2+8
=84+8
=92(米)
图形的周长是92米。
23.24米或21米的篱笆。
【分析】根据题目可知,长方形的篱笆一面靠墙,如果是长边靠墙,所需的篱笆长度两条宽加一条长;如果是短边靠墙,所需的篱笆长度是两条长加一条宽。
【详解】第一种情况:长边靠墙。如图:
那么所需的篱笆为:6+6+9=21(米)
第二种情况:短边靠墙。如图:
那么所需的篱笆为:9+9+6=24(米)
答:可能需要21米或24米篱笆。
【点睛】本题考察长方形的周长公式的实际应用,解题关键要注意一边靠墙不需要篱笆的情况。
24.(1)64分米
(2)24分米
【分析】(1)要在长20分米,宽16分米的长方形上划出最大的正方形,以长方形的宽为正方形的边长16分米,即是最大的正方形,计算出正方形的周长也是四周用木条固定的长度,据此解答。
(2)绣鸟区域是划出最大正方形以外的区域,是长方形,宽是(20-16)分米,长是16分米,注意长方形和正方形共用一条边,计算时可以先计算出长方形的周长再减去共用的边长16分米,即是绣鸟区周围要用的木条长度,据此解答。
【详解】(1)根据题意画图为:
最大正方形的周长:16×4=64(分米)
答:至少需要64分米木条。
(2)绣鸟区的宽是:20-16=4(分米),长是16分米;
绣鸟区长方形的周长:
(16+4)×2
=20×2
=40(分米)
绣鸟区需要的木条长:40-16=24(分米)
答:至少需要24分米木条。
【点睛】熟练掌握长方形及正方形周长公式的应用,注意计算绣鸟区需要的木条时,应减去共用的边长。
25.32厘米;40厘米
【分析】根据题图可知,拼成正方形的边长等于长方形的长,即8厘米。拼成长方形的长等于2个长方形的长,即2×8厘米,宽等于长方形的宽。根据正方形的周长=边长×4,长方形的周长=(长+宽)×2解答。
【详解】8×4=32(厘米)
(2×8+4)×2
=20×2
=40(厘米)
答:拼成正方形的周长为32厘米,长方形的周长为40厘米。
【点睛】解决本题的关键是明确正方形的边长以及长方形的长与宽,再根据正方形和长方形的周长公式解答。
26.10厘米
【分析】根据题意,以长方形的宽为最大正方形的边长3厘米,剪去后,剩下的图形是长方形,长是3厘米,宽是5-3=2厘米,根据长方形的周长=(长+宽)×2,计算解答。
【详解】根据题意,画图如下:
剩下图形的周长:
(3+2)×2
=5×2
=10(厘米)
答:剩下图形的周长是10厘米。
【点睛】本题的关键是明确剩下图形是长方形,并熟记长方形的周长公式。
27.36厘米;2个
【分析】根据题意,以长方形的宽为正方形的边长6厘米,两个大正方形相连,剪下的图形是长方形,长是6+6=12厘米,宽是6厘米,周长=(长+宽)×2;剩下长方形的长=26-12=14厘米,宽6厘米,再剪下边长是6厘米的正方形,看剩下长方形的长边有几个6厘米,6+6=12,12<14,够剪2个正方形,据此解答。
【详解】根据题意,画图如下:
剪下图形的周长:
(12+6)×2
=18×2
=36(厘米)
26-12=14(厘米)
6+6=12<14;还够剪2个大正方形。
答:剪下图形的周长是36厘米,剩下的彩纸还能剪2个最大的正方形。
【点睛】本题的关键是明确2个相连的大正方形就是长方形;以及剩下的长方形的长边里有几个6厘米。
28.56厘米;14厘米
【分析】根据“长方形的周长=(长+宽)×2”即可求出铁丝的长度,铁丝的长度除以4等于正方形的边长。
【详解】(18+10)×2
=28×2
=56(厘米)
56÷4=14(厘米)
答:这个框架的周长是56厘米,这个正方形的边长是14厘米。
【点睛】熟练运用长方形、正方形的周长公式是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三单元长方形和正方形易错题检测卷(单元测试)-小学数学三年级上册苏教版
一、选择题
1.把一个长为8厘米,宽为6厘米的长方形平均剪成两个长方形,周长比原来增加了( )厘米。
A.16 B.12 C.16或12
2.用两个边长4米的正方形拼成一个长方形,拼成的长方形周长是( )。
A.16米 B.24米 C.32米
3.学校篮球场长140米,宽20米,沿篮球场军官跑两圈是( )米。
A.200 B.320 C.640
4.下图中,甲乙两图形的周长相比,( )。
A.甲的周长长 B.乙的周长长 C.一样长
5.从一个长12厘米,宽9厘米的长方形纸片上剪下一个最大的正方形,正方形的边长是( )。
A.12厘米 B.3厘米 C.9厘米
6.在一张长18cm、宽10cm的长方形纸板上剪边长为3cm的小正方形,最多能剪( )个。
A.10 B.18 C.20
7.下图是分别用4个同样大小的正方形拼成的,周长最小的是( )。
A. B. C.
8.一个长方形的周长是24厘米,它的长和宽可能是( )。
A.8厘米和4厘米 B.8厘米和3厘米 C.6厘米和3厘米
二、填空题
9.用4个边长2厘米的小正方形拼成一个长方形或正方形,拼成的图形的周长可能是( )厘米,也可能是( )厘米。
10.小红用一根长120厘米的铁丝正好围成一个正方形,她围成的正方形的边长是( )厘米。如果这个正方形的每条边的长度都增加5厘米,那么这根铁丝的长度应增加( )厘米。
11.如图,一个长是15厘米,宽是10厘米的大长方形被分成了3个同样大的小长方形,小长方形的宽是( )厘米,周长是( )厘米。
12.一个长方形的长增加5厘米,宽增加3厘米,它的周长增加( )厘米。
13.一个长方形的周长是32厘米,宽是6厘米,长是( )厘米。
14.长方形游泳池长50米,宽30米,乐乐绕着游泳池走一圈,他走了( )米。
15.把一个长8厘米、宽4厘米的长方形,分成两个完全一样的小正方形,每个小正方形的周长是( )厘米;如果用4个边长是5厘米的小正方形,拼成一个大正方形,拼成的大正方形的周长是( )厘米。
16.两个长5厘米,宽2厘米的长方形拼成下面的图形,这个图形的周长是( )厘米。
三、判断题
17.一个长方形和一个正方形的周长相等,长方形的长是10厘米,宽是6厘米,那么正方形的边长是9厘米。( )
18.周长相等的两个长方形,它们各边的长也一定相同。( )
19.如左图,将一张长方形纸沿虚线对折,可以验证长方形的两条短边相等。( )
20.一个长方形菜地长55米,宽45米。妈妈沿着菜地跑一圈,跑了100米。( )
21.正方形的周长是4厘米,两个这样的正方形拼成的长方形周长是8厘米。( )
四、图形计算
22.计算下面各图形的周长。
五、解答题
23.张爷爷家有一块一面靠墙的菜地,长9米,宽6米,现在张爷爷要给这块菜地围上篱笆,可能需要多少米的篱笆?(先画一画,再算一算,写出两种答案)
24.苏绣起源于苏州吴县一带。它与湘绣、粤绣、蜀绣合称为中国“四大名绣”。张阿姨要绣一块长20分米,宽16分米的长方形苏绣。绣的时候在这块布上划出一块最大的正方形区域绣玫瑰花,其余的区域绣鸟。
(1)现在要在绣玫瑰花的区域四周用木条固定,至少需要多少分米木条?(先画示意图,再计算)
(2)如果要将绣鸟的区域周围也用木条固定,至少还需要多少分米木条?
25.用两个长8厘米、宽4厘米的长方形拼成正方形或长方形,拼成的正方形、长方形的周长各是多少厘米?
26.如图,有一张长方形纸,长是5厘米,宽是3厘米,从中剪下一个最大的正方形,剩下图形的周长是多少厘米?(先画一画,再算一算)
27.小兰有一张长26厘米,宽6厘米的长方形彩纸,她想从上面剪下2个相连的最大的正方形做手工,剪下图形的周长是多少厘米?剩下的彩纸还能剪几个最大的正方形?建议:先画一画,再算一算。
28.小明用一根铁丝做了一个长18厘米,宽10厘米的长方形框架,这个框架的周长是多少厘米?如果小明把它改围成正方形,这个正方形的边长是多少厘米?
参考答案:
1.C
【分析】如下图,横着剪成两个长方形,周长增加两个长的长度,即8×2=16(厘米),如果竖着剪成两个长方形,周长增加2个宽的长度,即6×2=12(厘米),据此即可解答。
【详解】根据分析可知,把一个长为8厘米,宽为6厘米的长方形平均剪成两个长方形,周长比原来增加了16或12厘米。
故答案为:C。
【点睛】把一个长方形平均剪成两个长方形可以横着剪,也可以竖着剪,两种剪法得到的长方形不一样。
2.B
【分析】用2个边长4米的小正方形拼成一个长方形,方法只有一种,摆成后的长方形的长是(4+4)米,宽是4米,长方形周长=(长+宽)×2,带入数据求解。
【详解】(4+4+4)×2
=12×2
=24(米)
故答案为:B
【点睛】本题的关键是求出拼成后长方形的长和宽,再根据长方形的周长公式进行计算。
3.C
【分析】篮球场的长加宽的和乘2等于篮球场的周长,再乘跑的圈数即可解答。
【详解】(140+20)×2×2
=160×4
=640(米)
故答案为:C。
【点睛】熟练掌握长方形的周长公式是解答本题的关键。
4.C
【分析】通过观察上图可知,长方形的对边相等,中间曲线段是甲乙两图形的公共边,所以甲乙两图形的周长相等。
【详解】根据分析可知,甲乙两图形的周长相等。
故答案为:C。
【点睛】本题主要考查学生的观察和分析问题的能力。
5.C
【详解】略
6.B
【分析】先用长除以3,再用宽除以3,然后把商相乘即可解答。
【详解】18÷3=6(个)
10÷3=3(个)……1(厘米)
6×3=18(个)
故答案为:B。
【点睛】先看长能剪几个3厘米的线段,宽能剪几个3厘米的线段,再作进一步解答。
7.C
【分析】分别计算出各图形的周长即可解答。
【详解】A.(4+1)×2=5×2=10
B.(3+1)×2+4=4×2+4=12
C.2×4=8
12>10>8,第3个图形的周长最小。
故答案为:C。
【点睛】本题主要考查学生对周长的认识。
8.A
【分析】根据长方形的周长=(长+宽)×2,所以:长+宽=长方形的周长÷2,即24÷2=12,然后将A、B、C三项各自的长和宽进行相加,等于12厘米的即可。
【详解】A.8+4=12(厘米);
B.8+3=11(厘米);
C.6+3=9(厘米)
故答案为:A
【点睛】本题考查了长方形的周长公式的掌握和灵活运用。
.
9. 20 16
【分析】根据题意:4个边长2厘米的正方形可以拼成一个长方形或正方形,长方形的周长:(长+宽)×2,带入即可,也可以拼成一个正方形,正方形的周长:边长×4,带入即可解答。
【详解】拼成一个长方形的周长是:
(8+2)×2
=10×2
=20(厘米);
拼成一个正方形的周长是:
(2+2)×4
=4×4
=16(厘米)
【点睛】根据题意进行拼组,然后根据长方形和正方形的周长计算公式,进行计算即可解答。
10. 30 20
【分析】根据题意可知,铁丝长度等于正方形的周长。根据正方形的边长=周长÷4,求出正方形的边长。根据正方形的周长=边长×4可知,每条边的长度都增加5厘米,周长增加4个5厘米。
【详解】120÷4=30(厘米)
则她围成的正方形的边长是30厘米。
5×4=20(厘米)
则这根铁丝的长度应增加20厘米。
【点睛】本题考查正方形周长公式的灵活运用。正方形的周长=边长×4,正方形的边长=周长÷4。
11. 5 30
【分析】观察图形可知:小长方形的长=大长方形的宽;小长方形的长=小长方形的两个宽;据此求出小长方形的长和宽,即可进行解答。
【详解】小长方形的宽:10÷2=5(厘米);
周长:(10+5)×2
=15×2
=30(厘米)
【点睛】观察图形求得小长方形的宽是解题关键。
12.16
【分析】根据长方形的可知,长方形有两个长和两个宽,则长增加5厘米,两个长久增加5×2=10厘米,宽增加3厘米,则两个宽就增加3×2=6厘米,即可求得周长增加的厘米数。
【详解】5×2=10(厘米);
3×2=6(厘米)
10+6=16(厘米)
【点睛】此题主要考查长方形的周长的灵活运用。
13.10
【分析】长方形的周长除以2,再减去宽的长度,等于长方形的长。
【详解】32÷2-6
=16-6
=10(厘米)
【点睛】熟练运用长方形的周长公式是解答本题的关键。
14.160
【分析】绕着游泳池走一圈即求长方形游泳池的周长,根据长方形的周长=(长+宽)×2,计算即可解答。
【详解】(50+30)×2
=80×2
=160(米)
【点睛】本题看出了长方形的周长的理解和灵活运用。
15. 16 40
【分析】根据题意,长方形的长8厘米刚好可以分成2个正方形的边长8÷2=4厘米,长方形的宽4厘米,为正方形另一边的边长,根据正方形的周长公式=边长×4,计算即可;
如果用4个边长5厘米的小正方形,拼成一个大正方形,大正方形的边长是2个小正方形的边长,即5×2=10厘米,根据正方形的周长公式,计算即可解答。
【详解】小正方的边长是4厘米;
小正方形的周长:4×4=16厘米;
大正方形的边长:5×2=10(厘米)
大正方形的周长:10×4=40(厘米)。
【点睛】本题的关键是明确正方形的边长是多少,并熟记正方形的周长公式。
16.24
【分析】根据题图可知,图形的周长比两个长方形的周长和少2个宽。根据长方形的周长=(长+宽)×2,求出长方形的周长。再乘2,求出2个长方形的周长和。再减去2个宽,即可求出图形的周长。
【详解】(5+2)×2×2-2×2
=7×2×2-2×2
=28-4
=24(厘米)
则这个图形的周长是24厘米。
【点睛】熟练掌握长方形的周长公式,灵活运用公式解决问题。
17.×
【分析】根据长方形的周长=(长+宽)×2,把数据代入公式求出长方形的周长,再根据正方形的边长=周长÷4,求出正方形的边长,然后与9厘米进行比较。
【详解】(10+6)×2÷4
=16×2÷4
=32÷4
=8(厘米)
则正方形的边长是8厘米,因此题干中的结论是错误的。
故答案为:×。
【点睛】此题主要考查长方形、正方形周长公式的灵活运用,关键是熟记公式。
18.×
【分析】长方形的周长=(长+宽)×2,当两个长方形的周长相等时,两个长方形的长与宽的和相等,不能确定两个长方形的长相等,宽相等,即两个长方形的形状相同。例如周长为16厘米的两个长方形,一个长5厘米、宽3厘米,另一个长6厘米、宽2厘米。据此判断即可。
【详解】根据分析可知,周长相等的两个长方形,它们各边的长不一定相同,故原题干说法错误。
故答案为:×
【点睛】熟记长方形的周长公式:长方形的周长=(长+宽)×2,长方形的周长大小和长与宽两个量有关。
19.×
【分析】按照如图方式对折,可以发现长方形的两条长边重合,可以验证长方形的两条长边相等。
【详解】按照图中的折叠方式,并不能验证长方形的两条短边相等;
题干阐述错误,故答案为:×。
【点睛】长方形的对边相等且互相平行,当长方形的一组邻边也相等时,将会变成正方形。
20.×
【分析】根据长方形的周长=(长+宽)×2即可求得菜地的周长,再与妈妈跑的路程比较即可解答。
【详解】(55+45)×2
=100×2
=200(米)
200米>100米;
故答案为:×
【点睛】掌握长方形的周长公式是解题的关键。
21.×
【分析】两个正方形拼成一个长方形,则长方形的长等于2个正方形的边长,宽等于正方形的边长。根据正方形的边长=周长÷4,求出正方形的边长。再根据长方形的周长=(长+宽)×2解答。
【详解】4÷4=1(厘米)
(2×1+1)×2
=3×2
=6(厘米)
则长方形的周长是6厘米。
所以原题说法错误。
故答案为:×
【点睛】本题关键是明确长方形的长与宽,再根据正方形和长方形的周长公式解答。
22.144分米;92米
【分析】(1)根据正方形的周长=边长×4,解答即可;
(2)
如图所示,将图形的边向上平移后可知,图形的周长等于长24米宽18米的长方形的周长,再加上两个4米,据此解答即可。
【详解】36×4=144(分米)
正方形的周长是144分米。
(24+18)×2+4×2
=42×2+8
=84+8
=92(米)
图形的周长是92米。
23.24米或21米的篱笆。
【分析】根据题目可知,长方形的篱笆一面靠墙,如果是长边靠墙,所需的篱笆长度两条宽加一条长;如果是短边靠墙,所需的篱笆长度是两条长加一条宽。
【详解】第一种情况:长边靠墙。如图:
那么所需的篱笆为:6+6+9=21(米)
第二种情况:短边靠墙。如图:
那么所需的篱笆为:9+9+6=24(米)
答:可能需要21米或24米篱笆。
【点睛】本题考察长方形的周长公式的实际应用,解题关键要注意一边靠墙不需要篱笆的情况。
24.(1)64分米
(2)24分米
【分析】(1)要在长20分米,宽16分米的长方形上划出最大的正方形,以长方形的宽为正方形的边长16分米,即是最大的正方形,计算出正方形的周长也是四周用木条固定的长度,据此解答。
(2)绣鸟区域是划出最大正方形以外的区域,是长方形,宽是(20-16)分米,长是16分米,注意长方形和正方形共用一条边,计算时可以先计算出长方形的周长再减去共用的边长16分米,即是绣鸟区周围要用的木条长度,据此解答。
【详解】(1)根据题意画图为:
最大正方形的周长:16×4=64(分米)
答:至少需要64分米木条。
(2)绣鸟区的宽是:20-16=4(分米),长是16分米;
绣鸟区长方形的周长:
(16+4)×2
=20×2
=40(分米)
绣鸟区需要的木条长:40-16=24(分米)
答:至少需要24分米木条。
【点睛】熟练掌握长方形及正方形周长公式的应用,注意计算绣鸟区需要的木条时,应减去共用的边长。
25.32厘米;40厘米
【分析】根据题图可知,拼成正方形的边长等于长方形的长,即8厘米。拼成长方形的长等于2个长方形的长,即2×8厘米,宽等于长方形的宽。根据正方形的周长=边长×4,长方形的周长=(长+宽)×2解答。
【详解】8×4=32(厘米)
(2×8+4)×2
=20×2
=40(厘米)
答:拼成正方形的周长为32厘米,长方形的周长为40厘米。
【点睛】解决本题的关键是明确正方形的边长以及长方形的长与宽,再根据正方形和长方形的周长公式解答。
26.10厘米
【分析】根据题意,以长方形的宽为最大正方形的边长3厘米,剪去后,剩下的图形是长方形,长是3厘米,宽是5-3=2厘米,根据长方形的周长=(长+宽)×2,计算解答。
【详解】根据题意,画图如下:
剩下图形的周长:
(3+2)×2
=5×2
=10(厘米)
答:剩下图形的周长是10厘米。
【点睛】本题的关键是明确剩下图形是长方形,并熟记长方形的周长公式。
27.36厘米;2个
【分析】根据题意,以长方形的宽为正方形的边长6厘米,两个大正方形相连,剪下的图形是长方形,长是6+6=12厘米,宽是6厘米,周长=(长+宽)×2;剩下长方形的长=26-12=14厘米,宽6厘米,再剪下边长是6厘米的正方形,看剩下长方形的长边有几个6厘米,6+6=12,12<14,够剪2个正方形,据此解答。
【详解】根据题意,画图如下:
剪下图形的周长:
(12+6)×2
=18×2
=36(厘米)
26-12=14(厘米)
6+6=12<14;还够剪2个大正方形。
答:剪下图形的周长是36厘米,剩下的彩纸还能剪2个最大的正方形。
【点睛】本题的关键是明确2个相连的大正方形就是长方形;以及剩下的长方形的长边里有几个6厘米。
28.56厘米;14厘米
【分析】根据“长方形的周长=(长+宽)×2”即可求出铁丝的长度,铁丝的长度除以4等于正方形的边长。
【详解】(18+10)×2
=28×2
=56(厘米)
56÷4=14(厘米)
答:这个框架的周长是56厘米,这个正方形的边长是14厘米。
【点睛】熟练运用长方形、正方形的周长公式是解答本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 两、三位数乘一位数
- 整十、整百数乘一位数的口算
- 倍的认识和有关倍的简单实际问题
- 两、三位数乘一位数(不进位)的笔算
- 两、三位数乘一位数(进位)的笔算
- 两、三位数乘一位数(连续进位)的笔算
- 乘数中间、末尾有0的乘法
- 二 千克和克
- 认识千克
- 认识克
- 三 长方形和正方形
- 长方形和正方形的基本特征
- 认识周长
- 长方形和正方形周长的计算
- 周长是多少
- 四 两、三位数除以一位数
- 两、三位数除以一位数的口算
- 两、三位数除以一位数(首位能整除)的笔算
- 除法的验算
- 两、三位数除以一位数(首位不能整除)的笔算
- 商中间、末尾有0的除法
- 五 解决问题的策略
- 间隔排列
- 六 平移、旋转和轴对称
- 七 分数的初步认识(一)
- 多彩的“分数条”
