人教版七年级上册1.4.1 有理数的乘法 课件(共24张PPT)
文档属性
| 名称 | 人教版七年级上册1.4.1 有理数的乘法 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 19:59:58 | ||
图片预览





文档简介
(共24张PPT)
第1章 有理数
1.4.2 有理数的除法
七年级数学上册·人教版
01
有理数的乘法
02
倒数的概念和计算
03
有理数乘法的运算律
04
有理数的除法
有理数的乘法
1
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
一直蜗牛沿直线爬行,起始时刻它的位置在点O
借助数轴来研究有理数乘法的法则
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
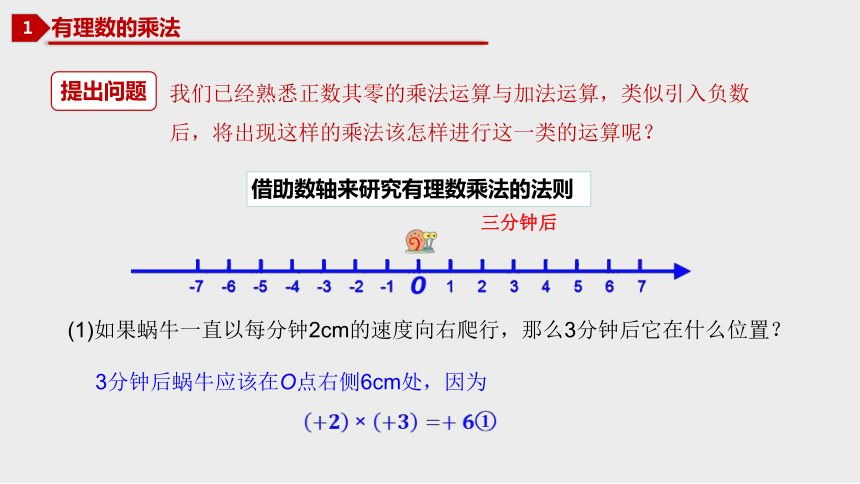
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟后它在什么位置?
借助数轴来研究有理数乘法的法则
3分钟后蜗牛应该在O点右侧6cm处,因为
①
三分钟后
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后它又在什么位置?
借助数轴来研究有理数乘法的法则
3分钟后蜗牛应该在O点左侧6cm处,因为
②
三分钟后
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
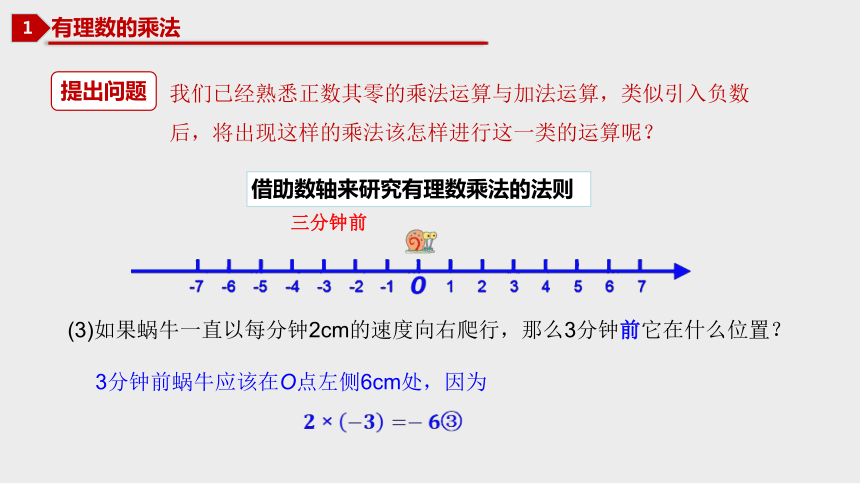
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟前它在什么位置?
借助数轴来研究有理数乘法的法则
3分钟前蜗牛应该在O点左侧6cm处,因为
③
三分钟前
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟前它在什么位置?
借助数轴来研究有理数乘法的法则
3分钟前蜗牛应该在O点右侧6cm处,因为
④
三分钟前
有理数的乘法
1
④
①
②
③
正数乘以正数的积为( )数
负数乘以正数的积为( )数
正数乘以负数的积为( )数
负数乘以负数的积为( )数
两个数相乘,乘积的绝对值等于各乘数绝对值的( )
正
正
负
负
积
有理数的乘法
1
有理数乘法法则
任何数同0相乘都得0
两数相乘的结果,同号为正,异号为负,并把绝对值相乘;
任何数与1相乘都等于它本身
任何数与-1相乘都等于它的相反数
有理数的乘法
1
有理数乘法法则
有理数相乘时,结果的正负号由负因数的个数(负号的个数)个数决定,如果负号是奇数个,那么两两抵消之后剩下一个,最后的结果带负号,是负值;如果负号是偶数个,那么负号刚好两两抵消,结果没有负号,是正值。举例如下:
共2个负号,结果为正,原式=3×5×2=30
共3个负号,结果为负,原式= - (2×3×4)=-24
共2018个负号,结果为正,原式=
有理数的乘法
1
1
有理数的乘法
1
2
倒数的概念和计算
2
倒数的概念和计算
2
观察
观察下列各组数的特点,可以给它们取个统一的名字吗?
观察到每组数字的分母和分子互相颠倒.
定义
如果两个数的乘积是1,那么就说它们互为倒数,并且一个数是另一个数的倒数.
即
倒数的概念和计算
2
互为倒数的两个数符号相同,即正数的倒数是正数,负数的倒数是复数
0 没有倒数,因为0不能做分母
倒数是相互的,当 时, 是 的倒数,同时 也是 的倒数
1和 -1的倒数是它们本身
倒数的概念和计算
2
1
倒数的概念和计算
2
2
有理数乘法的运算律
3
有理数乘法的运算律
3
问题①
计算下列各题,比较它们的结果,你有什么发现?
两个数相乘,交换因数的位置,积不变.
乘法交换律:
有理数乘法的运算律
3
问题②
计算下列各题,比较它们的结果,你有什么发现?
三个数相乘,先算前两个数相乘,或者先算后两个数相乘,积不变.
乘法结合律:
结合乘法交换律和乘法结合律可知:
多个数相乘,可以任意交换因数的位置和计算顺序,积不变.
有理数乘法的运算律
3
问题③
计算下列各题,比较它们的结果,你有什么发现?
一个数和另外两个数相乘,等于把这个数先分别与另外两个数相乘,所得的积再相加
乘法分配律:
有理数乘法的运算律
3
1
计算:
有理数乘法的运算律
3
2
用两种方法计算:
第1章 有理数
1.4.2 有理数的除法
七年级数学上册·人教版
01
有理数的乘法
02
倒数的概念和计算
03
有理数乘法的运算律
04
有理数的除法
有理数的乘法
1
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
一直蜗牛沿直线爬行,起始时刻它的位置在点O
借助数轴来研究有理数乘法的法则
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
(1)如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟后它在什么位置?
借助数轴来研究有理数乘法的法则
3分钟后蜗牛应该在O点右侧6cm处,因为
①
三分钟后
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
(2)如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟后它又在什么位置?
借助数轴来研究有理数乘法的法则
3分钟后蜗牛应该在O点左侧6cm处,因为
②
三分钟后
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
(3)如果蜗牛一直以每分钟2cm的速度向右爬行,那么3分钟前它在什么位置?
借助数轴来研究有理数乘法的法则
3分钟前蜗牛应该在O点左侧6cm处,因为
③
三分钟前
有理数的乘法
1
提出问题
我们已经熟悉正数其零的乘法运算与加法运算,类似引入负数后,将出现这样的乘法该怎样进行这一类的运算呢?
(4)如果蜗牛一直以每分钟2cm的速度向左爬行,那么3分钟前它在什么位置?
借助数轴来研究有理数乘法的法则
3分钟前蜗牛应该在O点右侧6cm处,因为
④
三分钟前
有理数的乘法
1
④
①
②
③
正数乘以正数的积为( )数
负数乘以正数的积为( )数
正数乘以负数的积为( )数
负数乘以负数的积为( )数
两个数相乘,乘积的绝对值等于各乘数绝对值的( )
正
正
负
负
积
有理数的乘法
1
有理数乘法法则
任何数同0相乘都得0
两数相乘的结果,同号为正,异号为负,并把绝对值相乘;
任何数与1相乘都等于它本身
任何数与-1相乘都等于它的相反数
有理数的乘法
1
有理数乘法法则
有理数相乘时,结果的正负号由负因数的个数(负号的个数)个数决定,如果负号是奇数个,那么两两抵消之后剩下一个,最后的结果带负号,是负值;如果负号是偶数个,那么负号刚好两两抵消,结果没有负号,是正值。举例如下:
共2个负号,结果为正,原式=3×5×2=30
共3个负号,结果为负,原式= - (2×3×4)=-24
共2018个负号,结果为正,原式=
有理数的乘法
1
1
有理数的乘法
1
2
倒数的概念和计算
2
倒数的概念和计算
2
观察
观察下列各组数的特点,可以给它们取个统一的名字吗?
观察到每组数字的分母和分子互相颠倒.
定义
如果两个数的乘积是1,那么就说它们互为倒数,并且一个数是另一个数的倒数.
即
倒数的概念和计算
2
互为倒数的两个数符号相同,即正数的倒数是正数,负数的倒数是复数
0 没有倒数,因为0不能做分母
倒数是相互的,当 时, 是 的倒数,同时 也是 的倒数
1和 -1的倒数是它们本身
倒数的概念和计算
2
1
倒数的概念和计算
2
2
有理数乘法的运算律
3
有理数乘法的运算律
3
问题①
计算下列各题,比较它们的结果,你有什么发现?
两个数相乘,交换因数的位置,积不变.
乘法交换律:
有理数乘法的运算律
3
问题②
计算下列各题,比较它们的结果,你有什么发现?
三个数相乘,先算前两个数相乘,或者先算后两个数相乘,积不变.
乘法结合律:
结合乘法交换律和乘法结合律可知:
多个数相乘,可以任意交换因数的位置和计算顺序,积不变.
有理数乘法的运算律
3
问题③
计算下列各题,比较它们的结果,你有什么发现?
一个数和另外两个数相乘,等于把这个数先分别与另外两个数相乘,所得的积再相加
乘法分配律:
有理数乘法的运算律
3
1
计算:
有理数乘法的运算律
3
2
用两种方法计算:
