数学人教A版(2019)选择性必修第一册3.3 直线与抛物线的位置关系(共13张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.3 直线与抛物线的位置关系(共13张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 23:03:36 | ||
图片预览

文档简介
(共13张PPT)
人教2019 A版 选择性必修 一
直线与抛物线的位置关系
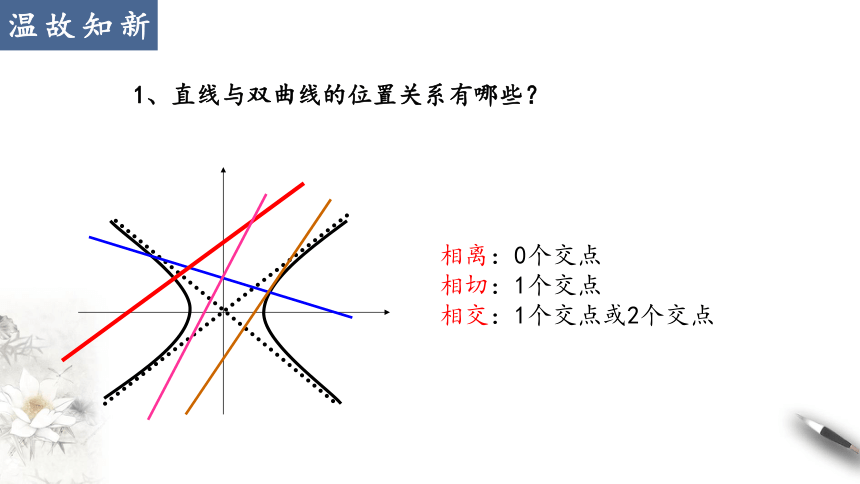
1、直线与双曲线的位置关系有哪些?
温故知新
相离:0个交点
相切:1个交点
相交:1个交点或2个交点
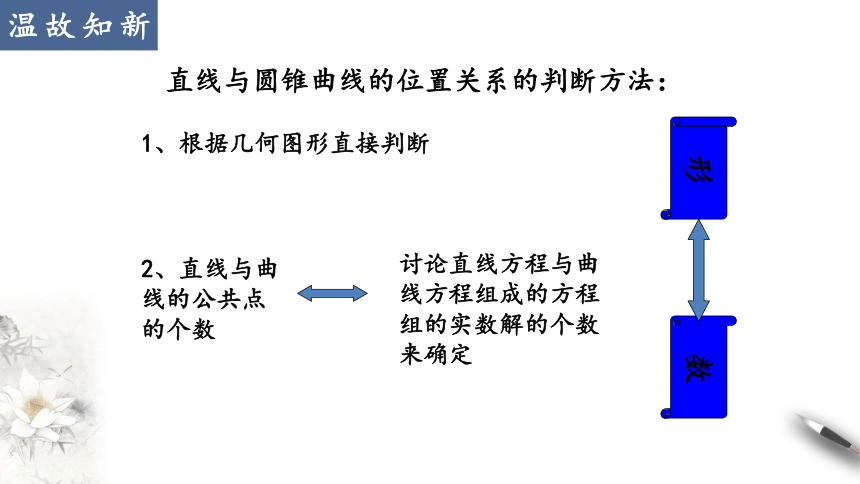
直线与圆锥曲线的位置关系的判断方法:
1、根据几何图形直接判断
2、直线与曲线的公共点的个数
讨论直线方程与曲线方程组成的方程组的实数解的个数来确定
形
数
温故知新
F
x
y
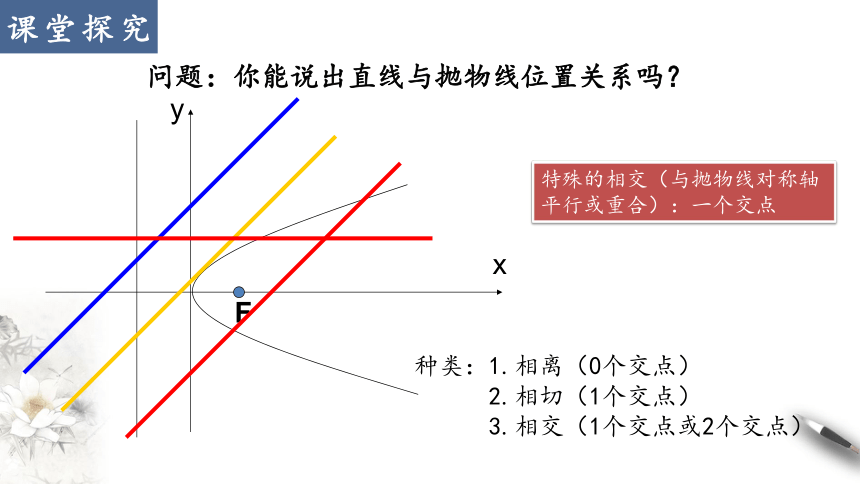
问题:你能说出直线与抛物线位置关系吗?
课堂探究
种类:1.相离(0个交点)
2.相切(1个交点)
3.相交(1个交点或2个交点)
特殊的相交(与抛物线对称轴平行或重合):一个交点
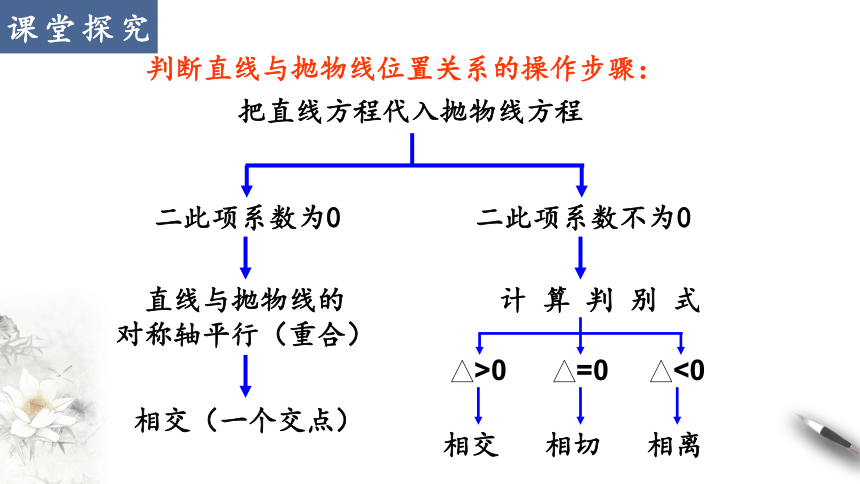
判断直线与抛物线位置关系的操作步骤:
把直线方程代入抛物线方程
二此项系数为0
二此项系数不为0
直线与抛物线的
对称轴平行(重合)
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
课堂探究
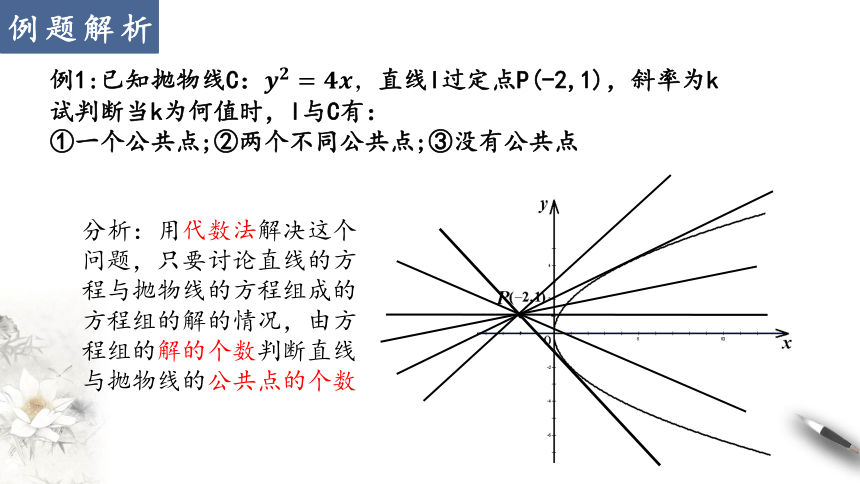
例1:已知抛物线C:,直线l过定点P(-2,1),斜率为k
试判断当k为何值时,l与C有:
①一个公共点;②两个不同公共点;③没有公共点
例题解析
例题解析
分析:用代数法解决这个问题,只要讨论直线的方程与抛物线的方程组成的方程组的解的情况,由方程组的解的个数判断直线与抛物线的公共点的个数
例1:已知抛物线C:,直线l过定点P(-2,1),斜率为k
试判断当k为何值时,l与C有:
①一个公共点;②两个不同公共点;③没有公共点
例题解析
例题解析
解:依题意直线l的方程为
联立
消去可得 (Ⅰ)
当k=0时,方程 (Ⅰ)只有一解,所以直线与抛物线只有一个公共点
当k≠0时,方程 (Ⅰ)的根的判别式
①当=0时,即k=-1或,方程 (Ⅰ)只有一解,直线与抛物线只有一个公共点
②当>0时,即-1<k<,方程 (Ⅰ)有两解,所以直线与抛物线有两个公共点
③当<0时,即k<-1或k>,方程 (Ⅰ)无解,所以直线与抛物线没有公共点
变式:过点M(0,1)与抛物线C:仅有一个公共点的直线方程是
巩固练习
.
F
解:过点(0,1)且斜率不存在的直线方程为x=0,与抛物线相切。
当过点(0,1)的直线斜率存在时,设其方程为
由,消去,得
当时,直线方程直线与抛物线相交
当时,若直线与抛物线相切,则,即,解得,所以直线方程为
故所求直线方程为或或
例题解析
例2、已知直线l:y=-x+1和抛物线C:y2=4x,设直线与抛物线的交点为A、B,求AB的长.
A
B
说明:同研究直线截椭圆或双曲线所得弦长的计算方法相同,设斜率为k的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则有弦长公式
例题解析
例3:过点Q(4,1)作抛物线的弦AB,恰被Q所平分,求AB所在的直线方程
弦中点问题的处理方法,通常利用“整体代换,设而不求”的思想(“韦达定理”或“点差法”)
设A(x1,y1),B(x2,y2),则有
两式相减并整理得:
又,所以
所以AB所在直线方程为
思考
求证:若M(x0,y0)是抛物线的弦AB的中点,则直线AB的斜率为
【证明】设A(x1,y1),B(x2,y2),则有
两式相减并整理得:
又,所以
作业布置
直线与抛物线的位置关系
(1)直线与抛物线有三种位置关系:相交、相切、相离
相交:直线与抛物线交于两个不同点,或直线与抛物线的对称轴平行;
相切:直线与抛物线有且只有一个公共点,且直线不平行于抛物线的对称轴,
相离:直线与抛物线无公共点
(2)直线与抛物线的位置关系的判断
把直线的方程和抛物线的方程联立得一方程组,于是:
①方程组有一组解 直线与抛物线相交或相切(1个公共点)
②方程组有两组解 直线与抛物线相交(2个公共点) ;
③方程组无解 直线与抛物线相离(0个公共点)
人教2019 A版 选择性必修 一
作业:课后作业相应习题
作业布置
人教2019 A版 选择性必修 一
直线与抛物线的位置关系
1、直线与双曲线的位置关系有哪些?
温故知新
相离:0个交点
相切:1个交点
相交:1个交点或2个交点
直线与圆锥曲线的位置关系的判断方法:
1、根据几何图形直接判断
2、直线与曲线的公共点的个数
讨论直线方程与曲线方程组成的方程组的实数解的个数来确定
形
数
温故知新
F
x
y
问题:你能说出直线与抛物线位置关系吗?
课堂探究
种类:1.相离(0个交点)
2.相切(1个交点)
3.相交(1个交点或2个交点)
特殊的相交(与抛物线对称轴平行或重合):一个交点
判断直线与抛物线位置关系的操作步骤:
把直线方程代入抛物线方程
二此项系数为0
二此项系数不为0
直线与抛物线的
对称轴平行(重合)
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
课堂探究
例1:已知抛物线C:,直线l过定点P(-2,1),斜率为k
试判断当k为何值时,l与C有:
①一个公共点;②两个不同公共点;③没有公共点
例题解析
例题解析
分析:用代数法解决这个问题,只要讨论直线的方程与抛物线的方程组成的方程组的解的情况,由方程组的解的个数判断直线与抛物线的公共点的个数
例1:已知抛物线C:,直线l过定点P(-2,1),斜率为k
试判断当k为何值时,l与C有:
①一个公共点;②两个不同公共点;③没有公共点
例题解析
例题解析
解:依题意直线l的方程为
联立
消去可得 (Ⅰ)
当k=0时,方程 (Ⅰ)只有一解,所以直线与抛物线只有一个公共点
当k≠0时,方程 (Ⅰ)的根的判别式
①当=0时,即k=-1或,方程 (Ⅰ)只有一解,直线与抛物线只有一个公共点
②当>0时,即-1<k<,方程 (Ⅰ)有两解,所以直线与抛物线有两个公共点
③当<0时,即k<-1或k>,方程 (Ⅰ)无解,所以直线与抛物线没有公共点
变式:过点M(0,1)与抛物线C:仅有一个公共点的直线方程是
巩固练习
.
F
解:过点(0,1)且斜率不存在的直线方程为x=0,与抛物线相切。
当过点(0,1)的直线斜率存在时,设其方程为
由,消去,得
当时,直线方程直线与抛物线相交
当时,若直线与抛物线相切,则,即,解得,所以直线方程为
故所求直线方程为或或
例题解析
例2、已知直线l:y=-x+1和抛物线C:y2=4x,设直线与抛物线的交点为A、B,求AB的长.
A
B
说明:同研究直线截椭圆或双曲线所得弦长的计算方法相同,设斜率为k的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则有弦长公式
例题解析
例3:过点Q(4,1)作抛物线的弦AB,恰被Q所平分,求AB所在的直线方程
弦中点问题的处理方法,通常利用“整体代换,设而不求”的思想(“韦达定理”或“点差法”)
设A(x1,y1),B(x2,y2),则有
两式相减并整理得:
又,所以
所以AB所在直线方程为
思考
求证:若M(x0,y0)是抛物线的弦AB的中点,则直线AB的斜率为
【证明】设A(x1,y1),B(x2,y2),则有
两式相减并整理得:
又,所以
作业布置
直线与抛物线的位置关系
(1)直线与抛物线有三种位置关系:相交、相切、相离
相交:直线与抛物线交于两个不同点,或直线与抛物线的对称轴平行;
相切:直线与抛物线有且只有一个公共点,且直线不平行于抛物线的对称轴,
相离:直线与抛物线无公共点
(2)直线与抛物线的位置关系的判断
把直线的方程和抛物线的方程联立得一方程组,于是:
①方程组有一组解 直线与抛物线相交或相切(1个公共点)
②方程组有两组解 直线与抛物线相交(2个公共点) ;
③方程组无解 直线与抛物线相离(0个公共点)
人教2019 A版 选择性必修 一
作业:课后作业相应习题
作业布置
