2022-2023学年高一年级北师大版(2019)数学必修一7.2.1 古典概型[课时练习](Word含答案)
文档属性
| 名称 | 2022-2023学年高一年级北师大版(2019)数学必修一7.2.1 古典概型[课时练习](Word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 170.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 00:00:00 | ||
图片预览


文档简介
7.2.1 古典概型
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共6小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
有5个条件类似的大学毕业生A,B,C,D,E应聘某两个相同的工作岗位,每个岗位只招聘1人,如果每个人被录用的机会相等,则学生A被录用的概率为( )
A. B. C. D.
下列试验中,是古典概型的为( )
A. 种下一粒花生,观察它是否发芽
B. 向正方形ABCD内任意投掷一点P,观察点P是否与正方形的中心O重合
C. 从1,2,3,4四个数中任取两个数,求所取两数之一是2的概率
D. 在区间[0,5]内任取一数,求此数小于2的概率
甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完若三人均领到整数元,且每人至少领到1元,则乙获得“手气最佳”(即乙领取的钱数不少于其他任何人)的概率是( )
A. B. C. D.
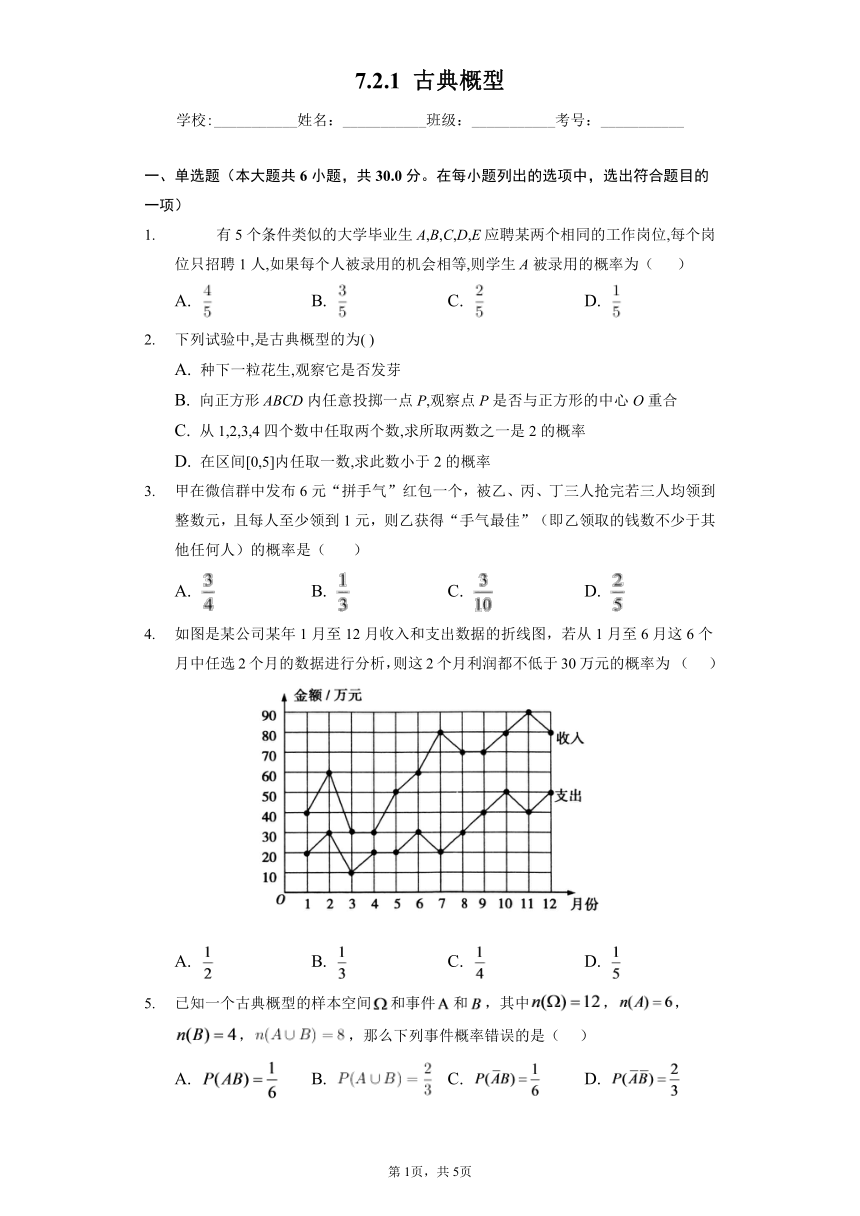
如图是某公司某年1月至12月收入和支出数据的折线图,若从1月至6月这6个月中任选2个月的数据进行分析,则这2个月利润都不低于30万元的概率为 ( )
A. B. C. D.
已知一个古典概型的样本空间和事件和,其中,,,,那么下列事件概率错误的是( )
A. B. C. D.
我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想的内容是:每个大于2的偶数都可以表示为两个素数的和,例如:(其中与算同一种方法),在大于4且不超过16的偶数中,随机选取两个不同的偶数,则两个偶数都可以有两种方法表示为两个素数的和的概率为( )
A. B. C. D.
二、多选题(本大题共1小题,共5.0分。在每小题有多项符合题目要求)
博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二中该嘉宾坐到“3号”车的概率分别为P1,P2,则 ( )
A. B. C. D. P1>P2
三、填空题(本大题共5小题,共25.0分)
从含有两件正品a1,a2和一件次品b的3件产品中,按先后顺序任意取出两件产品,每次取出后不放回,取出的两件产品都是正品的概率为 .
辽宁省2021年新高考采用“3+1+2”模式,其中“3”是指语文、数学、外语三门仍作为必考科目;“1”是指物理、历史作为选考科目,考生从中选择1门;“2”是指从生物、化学、地理、政治中选择2门作为选考科目.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生450人)中,采用分层随机抽样的方法抽取n名学生进行调查.若抽取的n名学生中有女生45人,则n的值为 ;若在抽取到的45名女生中,选择物理与选择历史的人数的比为2:1,为了解女生对历史的选课意向情况,现从45名女生中按分层随机抽样抽取6名女生,在这6名女生中再抽取3人,则在这3人中选择历史的人数为2的概率为 .
2022年冬奥会将在中国举行,现有一个工程需要两家企业联合建设,若有六家企业参与竞标,其中A企业来自陕西省,B,C两家企业来自天津市,D,E,F三家企业来自北京市,假设每家企业中标的概率相同,则在中标企业中,至少有一家来自北京市的概率是 .
某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.若从这6个国家中任选2个,则这2个国家都是亚洲国家的概率是 ;若从3个亚洲国家和3个欧洲国家中各选1个,则这2个国家包括A1但不包括B1的概率是 .
数学与文学有许多奇妙的联系,如诗中有回文诗:“儿忆父兮妻忆夫”,既可以顺读也可以逆读.数学中有回文数,如343,12521等,两位数的回文数有11,22,33,…,99共9个,则三位数的回文数中,偶数的概率是 .
四、解答题(本大题共3小题,共36.0分。解答应写出文字说明,证明过程或演算步骤)
(本小题12.0分)
为了解某地区中学生的身体发育状况,拟采用分层抽样的方法从甲、乙、丙三所中学抽取6个教学班进行调查.已知甲、乙、丙三所中学分别有12,6,18个教学班.
(Ⅰ)求从甲、乙、丙三所中学中分别抽取的教学班的个数;
(Ⅱ)若从抽取的6个教学班中随机抽取2个进行调查结果的对比,求这2个教学班中至少有1个来自甲学校的概率.
(本小题12.0分)
现有两个红球(记为,),两个白球(记为,),采用不放回简单随机抽样从中任意抽取两球.
(1)写出试验的样本空间;
(2)求恰好抽到一个红球一个白球的概率.
(本小题12.0分)
某校从高一年级学生中随机抽取40名学生,将他们期中考试的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
(1)求图中实数a的值;
(2)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2人,求这2名学生的数学成绩之差的绝对值不大于10的概率.
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】CD
8.【答案】
9.【答案】100
10.【答案】
11.【答案】
12.【答案】
13.【答案】解:(Ⅰ)由已知可知在甲、乙、丙三所中学共有教学班的比是12:6:18=2:1:3,
∴甲、乙、丙三所中学的教学班所占比例分别为,,,
所以甲学校抽取教学班数为6×个,乙学校抽取教学班数为6×个,丙学校抽取教学班数为6×个,
所以分别抽取的教学班个数为2,1,3.
(Ⅱ)由(Ⅰ)知,从甲、乙、丙三所中学分别抽取2,1,3个教学班,不妨分别记为A1,A2,B1,C1,C2,C3,
则从6个教学班中随机抽取2个教学班的样本空间为:Ω={(A1,A2),(A1,B1),(A1,C1),(A1,C2),(A1,C3),(A2,B1),(A2,C1),(A2,C2),(A2,C3),(B1,C1),(B1,C2),(B1,C3),(C1,C2),(C1,C3),(C2,C3)},其中共15个样本点,
设“从6个教学班中随机抽取2个教学班,至少有1个来自甲学校”为事件D
事件D={(A1,A2),(A1,B1),(A1,C1),(A1,C2),(A1,C3),(A2,B1),(A2,C1),(A2,C2),(A2,C3)},n(D)=9.
所以 P(D)===.
所以从抽取的6个教学班中随机抽取2个,且这2个教学班中至少有1个来自甲学校的概率为.
14.【答案】解:(1)两个红球(记为,),两个白球(记为,),
采用不放回简单随机抽样从中任意抽取两球,
则试验的样本空间.
(2)试验的样本空间,包含6个样本点,
其中恰好抽到一个红球一个白球包含4个样本点,
∴恰好抽到一个红球一个白球的概率.
15.【答案】解:(1)由题意,可得10(0.005+0.01+0.02+a+0.025+0.01)=1,解得a=0.03.
(2)成绩在[40,50)分数段内的有400.05=2(人),分别记为A,B;
成绩在[90,100]分数段内的有400.1=4(人),分别记为C,D,E,F.
则从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两人的样本空间
共15个样本点
如果这2名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,
那么这2名学生的数学成绩之差的绝对值一定不大于10.
如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,那么这2名学生的数学成绩之差的绝对值一定大于10.
记“这2名学生的数学成绩之差的绝对值不大于10”为事件M,
则,共7个样本点.
所以P(M)=.
即这2名学生的数学成绩之差的绝对值不大于10的概率为.
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共6小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
有5个条件类似的大学毕业生A,B,C,D,E应聘某两个相同的工作岗位,每个岗位只招聘1人,如果每个人被录用的机会相等,则学生A被录用的概率为( )
A. B. C. D.
下列试验中,是古典概型的为( )
A. 种下一粒花生,观察它是否发芽
B. 向正方形ABCD内任意投掷一点P,观察点P是否与正方形的中心O重合
C. 从1,2,3,4四个数中任取两个数,求所取两数之一是2的概率
D. 在区间[0,5]内任取一数,求此数小于2的概率
甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完若三人均领到整数元,且每人至少领到1元,则乙获得“手气最佳”(即乙领取的钱数不少于其他任何人)的概率是( )
A. B. C. D.
如图是某公司某年1月至12月收入和支出数据的折线图,若从1月至6月这6个月中任选2个月的数据进行分析,则这2个月利润都不低于30万元的概率为 ( )
A. B. C. D.
已知一个古典概型的样本空间和事件和,其中,,,,那么下列事件概率错误的是( )
A. B. C. D.
我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想的内容是:每个大于2的偶数都可以表示为两个素数的和,例如:(其中与算同一种方法),在大于4且不超过16的偶数中,随机选取两个不同的偶数,则两个偶数都可以有两种方法表示为两个素数的和的概率为( )
A. B. C. D.
二、多选题(本大题共1小题,共5.0分。在每小题有多项符合题目要求)
博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二中该嘉宾坐到“3号”车的概率分别为P1,P2,则 ( )
A. B. C. D. P1>P2
三、填空题(本大题共5小题,共25.0分)
从含有两件正品a1,a2和一件次品b的3件产品中,按先后顺序任意取出两件产品,每次取出后不放回,取出的两件产品都是正品的概率为 .
辽宁省2021年新高考采用“3+1+2”模式,其中“3”是指语文、数学、外语三门仍作为必考科目;“1”是指物理、历史作为选考科目,考生从中选择1门;“2”是指从生物、化学、地理、政治中选择2门作为选考科目.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生450人)中,采用分层随机抽样的方法抽取n名学生进行调查.若抽取的n名学生中有女生45人,则n的值为 ;若在抽取到的45名女生中,选择物理与选择历史的人数的比为2:1,为了解女生对历史的选课意向情况,现从45名女生中按分层随机抽样抽取6名女生,在这6名女生中再抽取3人,则在这3人中选择历史的人数为2的概率为 .
2022年冬奥会将在中国举行,现有一个工程需要两家企业联合建设,若有六家企业参与竞标,其中A企业来自陕西省,B,C两家企业来自天津市,D,E,F三家企业来自北京市,假设每家企业中标的概率相同,则在中标企业中,至少有一家来自北京市的概率是 .
某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.若从这6个国家中任选2个,则这2个国家都是亚洲国家的概率是 ;若从3个亚洲国家和3个欧洲国家中各选1个,则这2个国家包括A1但不包括B1的概率是 .
数学与文学有许多奇妙的联系,如诗中有回文诗:“儿忆父兮妻忆夫”,既可以顺读也可以逆读.数学中有回文数,如343,12521等,两位数的回文数有11,22,33,…,99共9个,则三位数的回文数中,偶数的概率是 .
四、解答题(本大题共3小题,共36.0分。解答应写出文字说明,证明过程或演算步骤)
(本小题12.0分)
为了解某地区中学生的身体发育状况,拟采用分层抽样的方法从甲、乙、丙三所中学抽取6个教学班进行调查.已知甲、乙、丙三所中学分别有12,6,18个教学班.
(Ⅰ)求从甲、乙、丙三所中学中分别抽取的教学班的个数;
(Ⅱ)若从抽取的6个教学班中随机抽取2个进行调查结果的对比,求这2个教学班中至少有1个来自甲学校的概率.
(本小题12.0分)
现有两个红球(记为,),两个白球(记为,),采用不放回简单随机抽样从中任意抽取两球.
(1)写出试验的样本空间;
(2)求恰好抽到一个红球一个白球的概率.
(本小题12.0分)
某校从高一年级学生中随机抽取40名学生,将他们期中考试的数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
(1)求图中实数a的值;
(2)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2人,求这2名学生的数学成绩之差的绝对值不大于10的概率.
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】CD
8.【答案】
9.【答案】100
10.【答案】
11.【答案】
12.【答案】
13.【答案】解:(Ⅰ)由已知可知在甲、乙、丙三所中学共有教学班的比是12:6:18=2:1:3,
∴甲、乙、丙三所中学的教学班所占比例分别为,,,
所以甲学校抽取教学班数为6×个,乙学校抽取教学班数为6×个,丙学校抽取教学班数为6×个,
所以分别抽取的教学班个数为2,1,3.
(Ⅱ)由(Ⅰ)知,从甲、乙、丙三所中学分别抽取2,1,3个教学班,不妨分别记为A1,A2,B1,C1,C2,C3,
则从6个教学班中随机抽取2个教学班的样本空间为:Ω={(A1,A2),(A1,B1),(A1,C1),(A1,C2),(A1,C3),(A2,B1),(A2,C1),(A2,C2),(A2,C3),(B1,C1),(B1,C2),(B1,C3),(C1,C2),(C1,C3),(C2,C3)},其中共15个样本点,
设“从6个教学班中随机抽取2个教学班,至少有1个来自甲学校”为事件D
事件D={(A1,A2),(A1,B1),(A1,C1),(A1,C2),(A1,C3),(A2,B1),(A2,C1),(A2,C2),(A2,C3)},n(D)=9.
所以 P(D)===.
所以从抽取的6个教学班中随机抽取2个,且这2个教学班中至少有1个来自甲学校的概率为.
14.【答案】解:(1)两个红球(记为,),两个白球(记为,),
采用不放回简单随机抽样从中任意抽取两球,
则试验的样本空间.
(2)试验的样本空间,包含6个样本点,
其中恰好抽到一个红球一个白球包含4个样本点,
∴恰好抽到一个红球一个白球的概率.
15.【答案】解:(1)由题意,可得10(0.005+0.01+0.02+a+0.025+0.01)=1,解得a=0.03.
(2)成绩在[40,50)分数段内的有400.05=2(人),分别记为A,B;
成绩在[90,100]分数段内的有400.1=4(人),分别记为C,D,E,F.
则从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两人的样本空间
共15个样本点
如果这2名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,
那么这2名学生的数学成绩之差的绝对值一定不大于10.
如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,那么这2名学生的数学成绩之差的绝对值一定大于10.
记“这2名学生的数学成绩之差的绝对值不大于10”为事件M,
则,共7个样本点.
所以P(M)=.
即这2名学生的数学成绩之差的绝对值不大于10的概率为.
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
