2022-2023学年高一年级北师大版(2019)数学必修一6.3.2 频率分布直方图[课时练习](Word含答案)
文档属性
| 名称 | 2022-2023学年高一年级北师大版(2019)数学必修一6.3.2 频率分布直方图[课时练习](Word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 390.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-02 07:33:30 | ||
图片预览


文档简介
6.3.2 频率分布直方图
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共5小题,共25.0分。在每小题列出的选项中,选出符合题目的一项)
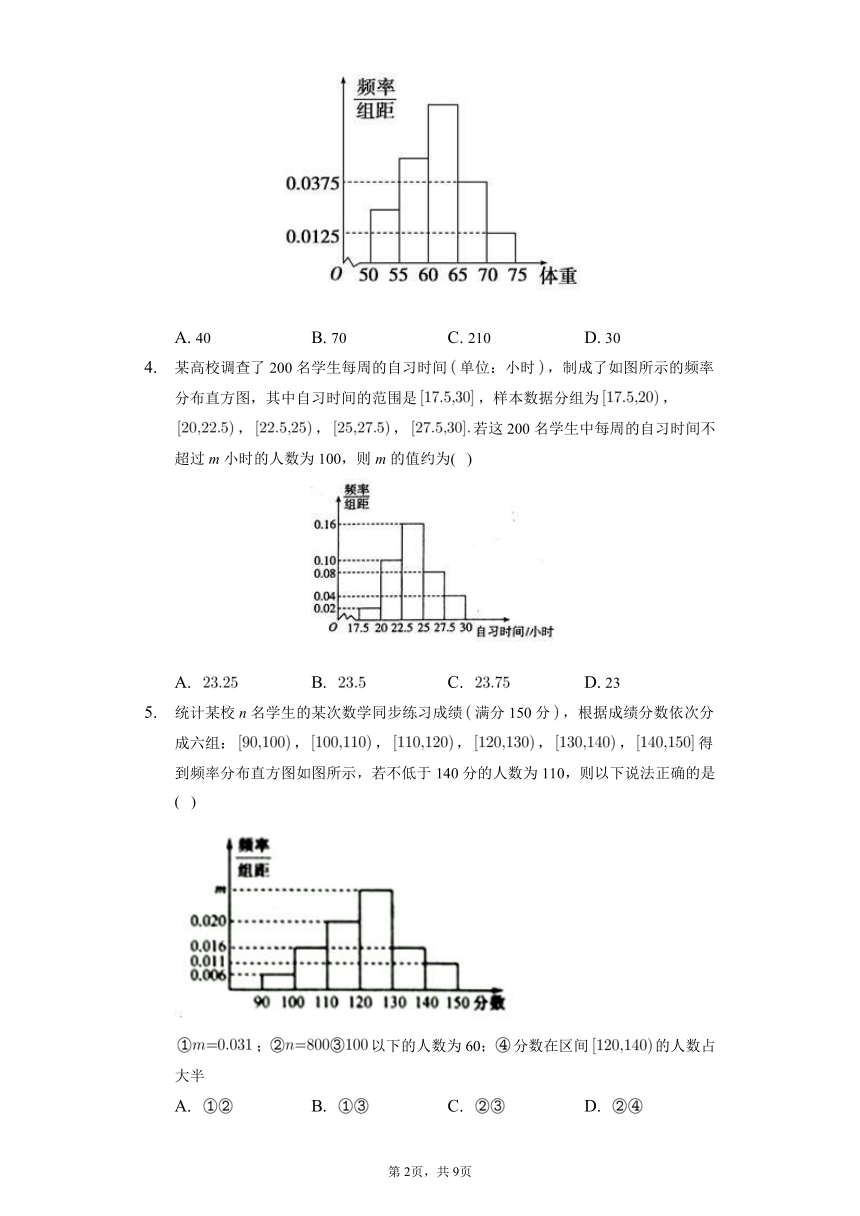
样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是( )
A. 32,0.4 B. 8,0.1 C. 32,0.1 D. 8,0.4
为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据的分组区间为将其按从左到右的顺序分别变为第一组,第二组.........,第五组,如图是根据试验数据制成的直方图,已知第二组有32人,第三组中有疗效的人数为67,则第三组中没有疗效的人数为( )
A. 3 B. 4 C. 5 D. 6
为了解某校高三学生身体状况,采用分层抽样的方法从本年级学生中随机抽取部分男生和女生进行体重测量,并将男生体重数据整理后,得到如图所示的频率分布直方图,已知从左到右前三个小组频率之比为,第二小组频数为10,已知年级中男、女生比例为,则从该年级中抽取的学生总数为( )
A. 40 B. 70 C. 210 D. 30
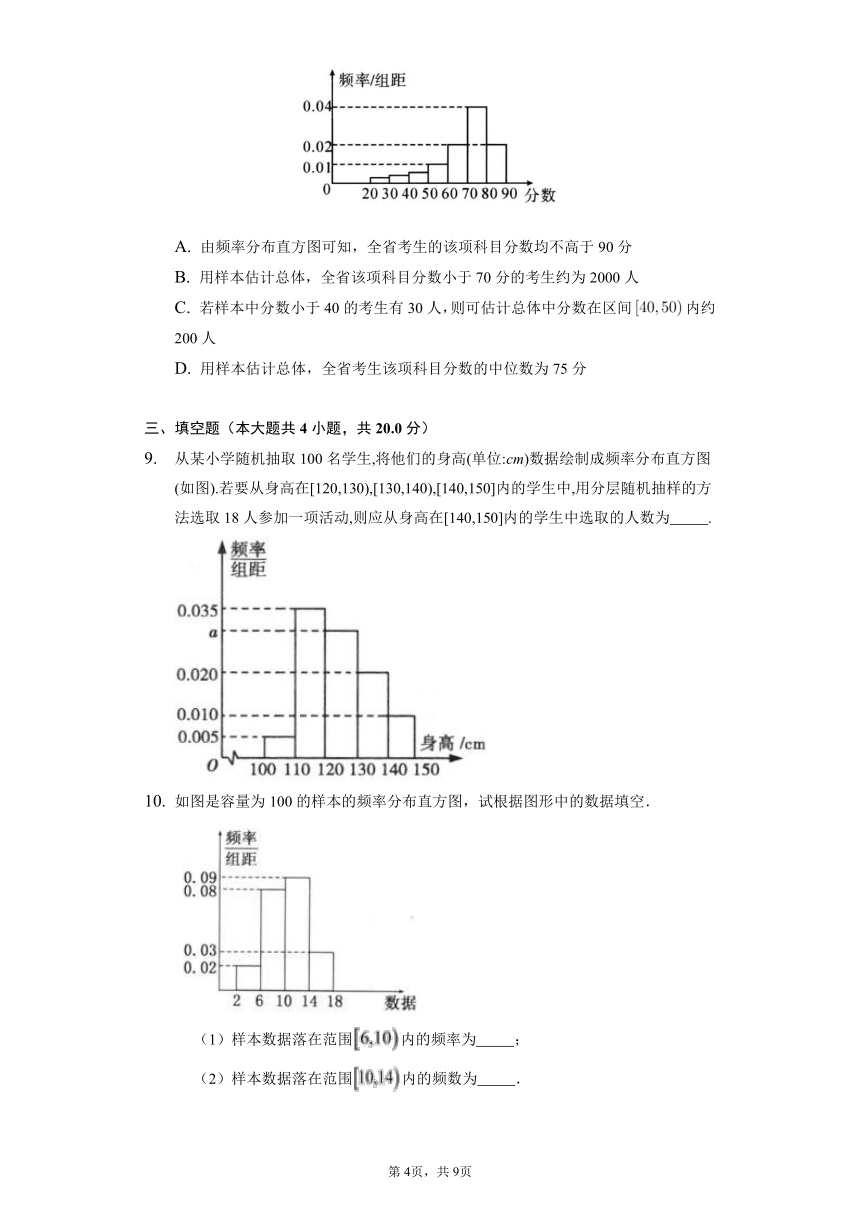
某高校调查了200名学生每周的自习时间单位:小时,制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,若这200名学生中每周的自习时间不超过m小时的人数为100,则m的值约为( )
A. B. C. D. 23
统计某校n名学生的某次数学同步练习成绩满分150分,根据成绩分数依次分成六组:,,,,,得到频率分布直方图如图所示,若不低于140分的人数为110,则以下说法正确的是( )
;以下的人数为60;分数在区间的人数占大半
A. B. C. D.
二、多选题(本大题共3小题,共15.0分。在每小题有多项符合题目要求)
为征求个人所得税法修改建议,某机构调查了10000名当地职工的月收入情况,并根据所得数据画出了样本的频率分布直方图.
下列说法正确的是( )
A. 月收入低于5000元的职工有5500名
B. 如果个税起征点调整至5000元,估计有50%的当地职工会被征税
C. 月收入高于或等于7000元的职工约为当地职工的5%
D. 根据此次调查,为使60%以上的职工不用缴纳个税,起征点应位于[5000,6000)内
为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,现调查了当地的100家中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,则下面结论正确的是()
A. 样本在区间[500, 700]内的频数为18
B. 如果规定年收入在300 万元以内的企业才能享受减免税政策,估计有30% 的当地中小型企业能享受到减免税政策
C. 样本的中位数小于350 万元
D. 可估计当地的中小型企业年收入的平均数超过400 万元(同一组中的数据用该组区间的中点值为代表)
某省2021年美术联考约有5000名学生参加,现从考试的科目素描(满分100分)中随机抽取了500名考生的考试成绩,记录他们的分数后,将数据分成7组:,,,,并整理得到如图所示的频率分布直方图.则下列说法不正确的是( )
A. 由频率分布直方图可知,全省考生的该项科目分数均不高于90分
B. 用样本估计总体,全省该项科目分数小于70分的考生约为2000人
C. 若样本中分数小于40的考生有30人,则可估计总体中分数在区间内约200人
D. 用样本估计总体,全省考生该项科目分数的中位数为75分
三、填空题(本大题共4小题,共20.0分)
从某小学随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]内的学生中,用分层随机抽样的方法选取18人参加一项活动,则应从身高在[140,150]内的学生中选取的人数为 .
如图是容量为100的样本的频率分布直方图,试根据图形中的数据填空.
(1)样本数据落在范围内的频率为 ;
(2)样本数据落在范围内的频数为 .
我国在贵州省平塘县修建的500米口径球面射电望远镜(FAST)是目前世界上最大单口径射电望远镜.截至2019年8月28日,该射电望远镜已发现132颗优质的脉冲星候选体,其中有93颗已被确认为新发现的脉冲星.脉冲星就是旋转的中子星,每一颗脉冲星每两脉冲间隔时间(脉冲星的自转周期)是一定的,最小的自转周期小到0.0014秒,最长的也不过11.765735秒.某天文研究机构观测并统计了93颗已被确认为新发现的脉冲星的自转周期,绘制了如图所示的频率分布直方图.在93颗新发现的脉冲星中,自转周期在2秒至10秒的颗数大约为 .
交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示,用分层随机抽样的方法从交通指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,则中度拥堵的路段应抽取 个.
四、解答题(本大题共3小题,共36.0分。解答应写出文字说明,证明过程或演算步骤)
(本小题12.0分)
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图),已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?共有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?
(本小题12.0分)
某公司计划购买1台机器,该种机器使用三年后即被淘汰机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元在机器使用期间,如果备件不足再购买,则每个500元现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得如图柱状图:
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用单位:元,n表示购机的同时购买的易损零件数.
1若,求y与x的函数解析式;
2若要求“需更换的易损零件数不大于n”的频率不小于,求n的最小值;
3假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
(本小题12.0分)
某电视台随机在本省内15~65岁的人群中抽取了n人回答问题“本省内著名旅游景点有哪些”,统计结果如图表所示.
组号 分组 回答正确
的人数 回答正确的人数占本
组的频率
第1组 [15,25) a 0.5
第2组 [25,35) 18 x
第3组 [35,45) b 0.9
第4组 [45,55) 9 0.36
第5组 [55,65] 3 y
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层随机抽样的方法抽取6人,求第2,3,4组每组各抽取多少人
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】ACD
7.【答案】AB
8.【答案】AD
9.【答案】3
10.【答案】0.32
36
11.【答案】79
12.【答案】3
13.【答案】解:(1)因为,
所以本次活动共有60件作品参加评比.
(2)由频率分布直方图可以看出第六组上交的作品数量最多,
因为,
所以第四组上交的作品数量最多,共有18件.
(3)第六组上交的作品数量为,
第六组的获奖率为,
第四组获奖率为,
又,
所以第六组获奖率高.
14.【答案】解:(1)当n=19时,
y=
=.
(2)由柱状图知,更换的易损零件数为16个频率为0.06,
更换的易损零件数为17个频率为0.16,
更换的易损零件数为18个频率为0.24,
更换的易损零件数为19个频率为0.24
又∵更换易损零件不大于n的频率为不小于0.5.
且
则n≥19 ,
∴n的最小值为19件;
(3)假设这100台机器在购机的同时每台都购买19个易损零件,
所须费用平均数为:(70×19×200+4300×20+4800×10)=4000(元),
假设这100台机器在购机的同时每台都购买20个易损零件,
所须费用平均数为(90×4000+10×4500)=4050(元),
∵4000<4050 ,
∴购买1台机器的同时应购买19台易损零件.
15.【答案】解:(1)由频率分布表中第4组数据可知,第4组总人数为9÷0.36=25,
再结合频率分布直方图可知n=25÷(0.025×10)=100,
∴a=100×0.01×10×0.5=5,
b=100×0.03×10×0.9=27,
x=18÷(100×0.020×10)=0.9,
y=3÷(100×0.015×10)=0.2
(2)第2,3,4组回答正确的共有54人.
∴利用分层抽样在54人中抽取6人,每组分别抽取的人数为:
第2组×6=2(人),第3组×6=3(人),第4组×6=1(人).
第2页,共2页
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共5小题,共25.0分。在每小题列出的选项中,选出符合题目的一项)
样本容量为100的频率分布直方图如图所示.根据样本的频率分布直方图估计样本数据落在[6,10)内的频数为a,样本数据落在[2,10)内的频率为b,则a,b分别是( )
A. 32,0.4 B. 8,0.1 C. 32,0.1 D. 8,0.4
为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据的分组区间为将其按从左到右的顺序分别变为第一组,第二组.........,第五组,如图是根据试验数据制成的直方图,已知第二组有32人,第三组中有疗效的人数为67,则第三组中没有疗效的人数为( )
A. 3 B. 4 C. 5 D. 6
为了解某校高三学生身体状况,采用分层抽样的方法从本年级学生中随机抽取部分男生和女生进行体重测量,并将男生体重数据整理后,得到如图所示的频率分布直方图,已知从左到右前三个小组频率之比为,第二小组频数为10,已知年级中男、女生比例为,则从该年级中抽取的学生总数为( )
A. 40 B. 70 C. 210 D. 30
某高校调查了200名学生每周的自习时间单位:小时,制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,若这200名学生中每周的自习时间不超过m小时的人数为100,则m的值约为( )
A. B. C. D. 23
统计某校n名学生的某次数学同步练习成绩满分150分,根据成绩分数依次分成六组:,,,,,得到频率分布直方图如图所示,若不低于140分的人数为110,则以下说法正确的是( )
;以下的人数为60;分数在区间的人数占大半
A. B. C. D.
二、多选题(本大题共3小题,共15.0分。在每小题有多项符合题目要求)
为征求个人所得税法修改建议,某机构调查了10000名当地职工的月收入情况,并根据所得数据画出了样本的频率分布直方图.
下列说法正确的是( )
A. 月收入低于5000元的职工有5500名
B. 如果个税起征点调整至5000元,估计有50%的当地职工会被征税
C. 月收入高于或等于7000元的职工约为当地职工的5%
D. 根据此次调查,为使60%以上的职工不用缴纳个税,起征点应位于[5000,6000)内
为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,现调查了当地的100家中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,则下面结论正确的是()
A. 样本在区间[500, 700]内的频数为18
B. 如果规定年收入在300 万元以内的企业才能享受减免税政策,估计有30% 的当地中小型企业能享受到减免税政策
C. 样本的中位数小于350 万元
D. 可估计当地的中小型企业年收入的平均数超过400 万元(同一组中的数据用该组区间的中点值为代表)
某省2021年美术联考约有5000名学生参加,现从考试的科目素描(满分100分)中随机抽取了500名考生的考试成绩,记录他们的分数后,将数据分成7组:,,,,并整理得到如图所示的频率分布直方图.则下列说法不正确的是( )
A. 由频率分布直方图可知,全省考生的该项科目分数均不高于90分
B. 用样本估计总体,全省该项科目分数小于70分的考生约为2000人
C. 若样本中分数小于40的考生有30人,则可估计总体中分数在区间内约200人
D. 用样本估计总体,全省考生该项科目分数的中位数为75分
三、填空题(本大题共4小题,共20.0分)
从某小学随机抽取100名学生,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]内的学生中,用分层随机抽样的方法选取18人参加一项活动,则应从身高在[140,150]内的学生中选取的人数为 .
如图是容量为100的样本的频率分布直方图,试根据图形中的数据填空.
(1)样本数据落在范围内的频率为 ;
(2)样本数据落在范围内的频数为 .
我国在贵州省平塘县修建的500米口径球面射电望远镜(FAST)是目前世界上最大单口径射电望远镜.截至2019年8月28日,该射电望远镜已发现132颗优质的脉冲星候选体,其中有93颗已被确认为新发现的脉冲星.脉冲星就是旋转的中子星,每一颗脉冲星每两脉冲间隔时间(脉冲星的自转周期)是一定的,最小的自转周期小到0.0014秒,最长的也不过11.765735秒.某天文研究机构观测并统计了93颗已被确认为新发现的脉冲星的自转周期,绘制了如图所示的频率分布直方图.在93颗新发现的脉冲星中,自转周期在2秒至10秒的颗数大约为 .
交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为T,其范围为[0,10],分别有五个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示,用分层随机抽样的方法从交通指数在[4,6),[6,8),[8,10]的路段中共抽取6个路段,则中度拥堵的路段应抽取 个.
四、解答题(本大题共3小题,共36.0分。解答应写出文字说明,证明过程或演算步骤)
(本小题12.0分)
在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图),已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?共有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高?
(本小题12.0分)
某公司计划购买1台机器,该种机器使用三年后即被淘汰机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元在机器使用期间,如果备件不足再购买,则每个500元现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得如图柱状图:
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用单位:元,n表示购机的同时购买的易损零件数.
1若,求y与x的函数解析式;
2若要求“需更换的易损零件数不大于n”的频率不小于,求n的最小值;
3假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
(本小题12.0分)
某电视台随机在本省内15~65岁的人群中抽取了n人回答问题“本省内著名旅游景点有哪些”,统计结果如图表所示.
组号 分组 回答正确
的人数 回答正确的人数占本
组的频率
第1组 [15,25) a 0.5
第2组 [25,35) 18 x
第3组 [35,45) b 0.9
第4组 [45,55) 9 0.36
第5组 [55,65] 3 y
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层随机抽样的方法抽取6人,求第2,3,4组每组各抽取多少人
1.【答案】A
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】ACD
7.【答案】AB
8.【答案】AD
9.【答案】3
10.【答案】0.32
36
11.【答案】79
12.【答案】3
13.【答案】解:(1)因为,
所以本次活动共有60件作品参加评比.
(2)由频率分布直方图可以看出第六组上交的作品数量最多,
因为,
所以第四组上交的作品数量最多,共有18件.
(3)第六组上交的作品数量为,
第六组的获奖率为,
第四组获奖率为,
又,
所以第六组获奖率高.
14.【答案】解:(1)当n=19时,
y=
=.
(2)由柱状图知,更换的易损零件数为16个频率为0.06,
更换的易损零件数为17个频率为0.16,
更换的易损零件数为18个频率为0.24,
更换的易损零件数为19个频率为0.24
又∵更换易损零件不大于n的频率为不小于0.5.
且
则n≥19 ,
∴n的最小值为19件;
(3)假设这100台机器在购机的同时每台都购买19个易损零件,
所须费用平均数为:(70×19×200+4300×20+4800×10)=4000(元),
假设这100台机器在购机的同时每台都购买20个易损零件,
所须费用平均数为(90×4000+10×4500)=4050(元),
∵4000<4050 ,
∴购买1台机器的同时应购买19台易损零件.
15.【答案】解:(1)由频率分布表中第4组数据可知,第4组总人数为9÷0.36=25,
再结合频率分布直方图可知n=25÷(0.025×10)=100,
∴a=100×0.01×10×0.5=5,
b=100×0.03×10×0.9=27,
x=18÷(100×0.020×10)=0.9,
y=3÷(100×0.015×10)=0.2
(2)第2,3,4组回答正确的共有54人.
∴利用分层抽样在54人中抽取6人,每组分别抽取的人数为:
第2组×6=2(人),第3组×6=3(人),第4组×6=1(人).
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
