13.3.2等边三角形课件
文档属性
| 名称 | 13.3.2等边三角形课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-29 00:00:00 | ||
图片预览



文档简介
课件19张PPT。13.3.2
等边三角形学习目标
1.理解并掌握等边三角形的定义,探索等边三角形的性质和判定方法,能够用等边三角形的知识解决相应的数学问题。
2.掌握含30o角的直角三角形的性质,并能灵活运用这一性质解决实际问题。
学习重难点
1.重点难点等边三角形性质和判定的应用。
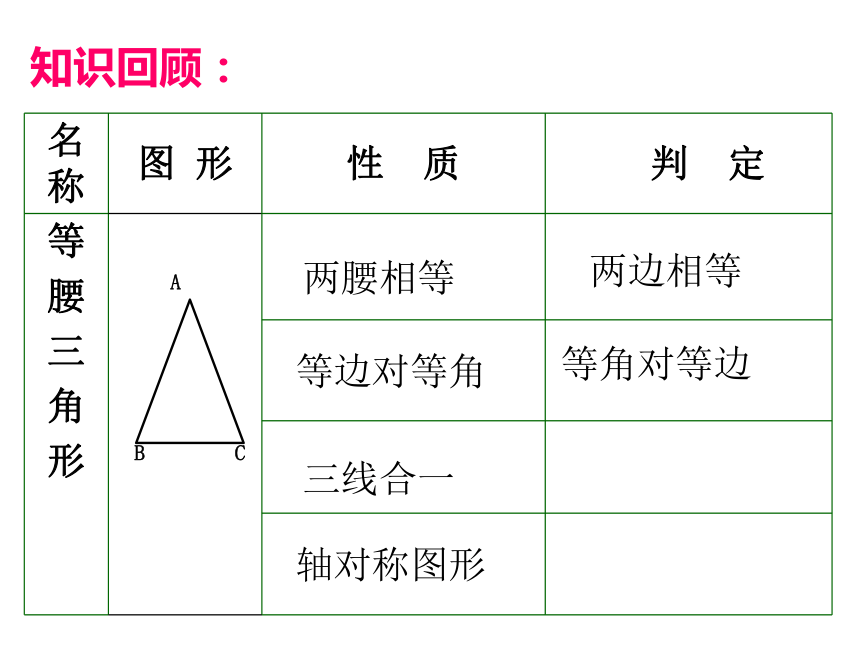
2.含30°角的直角三角形的性质定理的应用。等边对等角三线合一等角对等边两边相等两腰相等轴对称图形知识回顾: 在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等。 我们把三条边都相等的三角形叫做等边三角形(正三角形)。学习概念:等边三角形1、等边三角形的内角什么关系? 为什么?∵ AB=AC=BC
∴ ∠A=∠B=∠C(等边对等角)
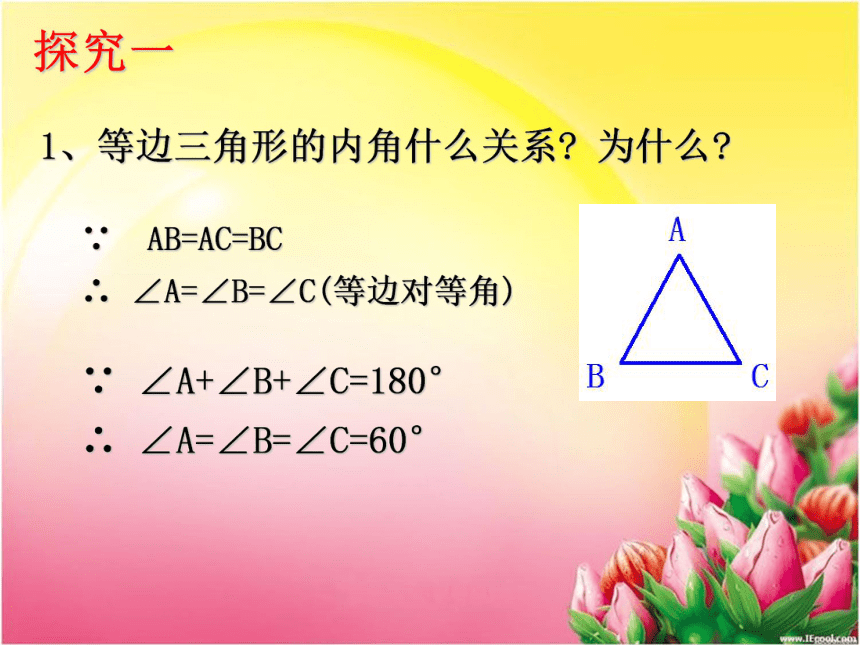
∵ ∠A+∠B+∠C=180°
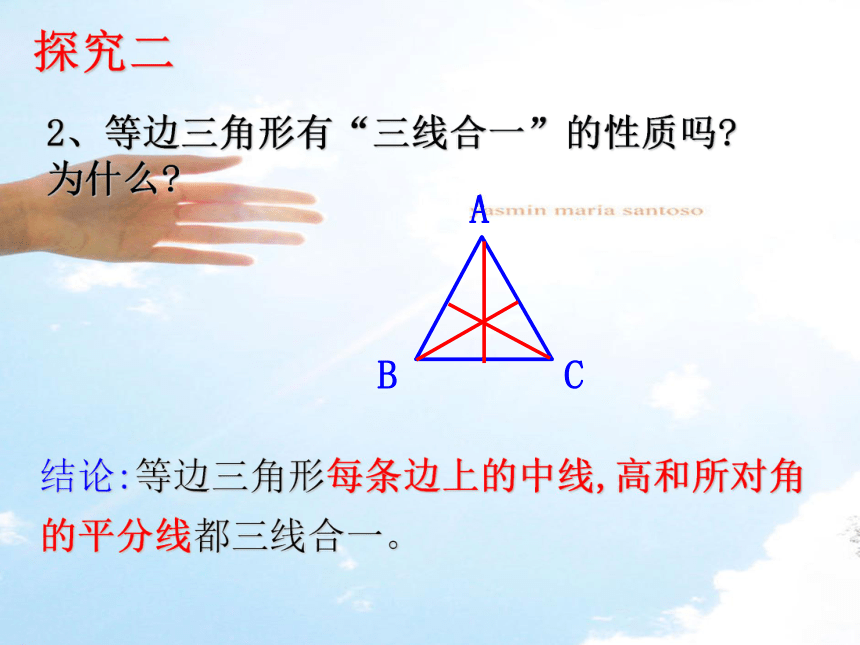
∴ ∠A=∠B=∠C=60°探究一2、等边三角形有“三线合一”的性质吗?
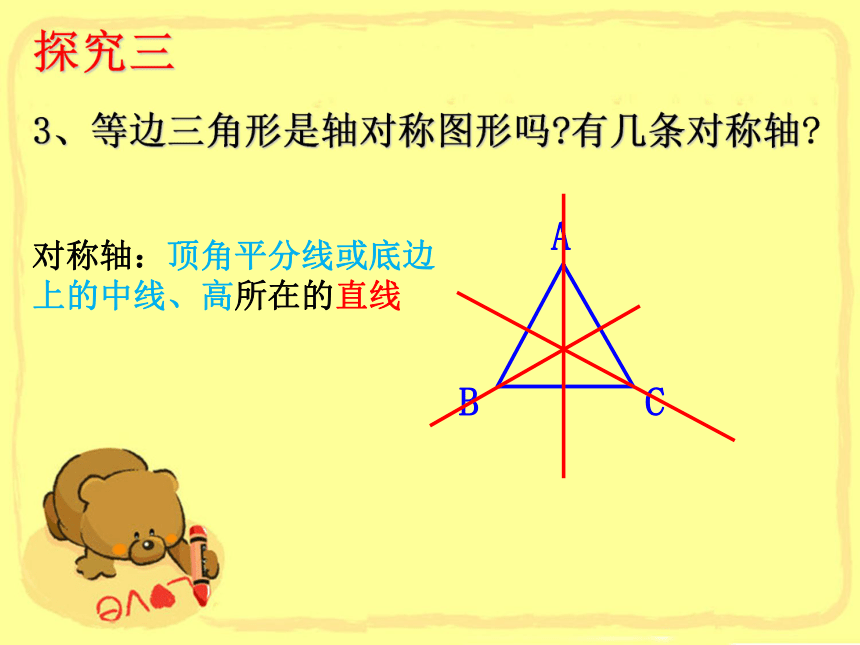
为什么?结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。探究二3、等边三角形是轴对称图形吗?有几条对称轴?探究三对称轴:顶角平分线或底边上的中线、高所在的直线等边三角形的性质2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.4.等边三角形是轴对称图形,有三条对称轴.
1 .三条边相等小 结 :1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.牛刀小试等边603 4、已知△ABC中,∠A=∠B=60°,AB=3cm 则△ABC的周长________5、 △ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______9cm5cm⒈ 三个角都相等的三角形是等边三角形.⒉ 有一个角是60°的等腰三角形是等边三角形.一个三角形满足什么条件就是等边三角形?探究四在等边三角形ABC的边,AB 、AC上分别截取AD=AE, 三角形ADE是什么三角形?说明理由。典例分析一 答:是等边三角形。证明:∵⊿ABC是等边三角形,
∴∠A=∠B=∠C=60°
∵AD=AE
∴⊿ADE是等边三角形。(有一个角是60°的等腰三角形是等边三角形)探究五 将两个含有板有30°的三角尺如图摆放在一起你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?∵△ABC与△ADC关于AC轴对称
∴AB=AD
△ABD是等边三角形
又∵AC⊥BD∴BC=DC=1/2AB探索分析: 解:∵DE⊥AC,BC⊥AC,∠A=30°
∴BC=1/2AB,DE=1/2AD
∴BC=1/2×10=5(m)
又∵AD=1/2AB
∴DE=1/2AD=1/2×5=2.5(m)
答:立柱BC的长上5m,DE的长是2.5m. 下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=10m,∠A=30°,立柱BC,DE要多长?典例分析二1.△ABC是等边三角形,D为AC的中点,延长BC到E,使CE=CD,
求证:BD=DE.提示:证明∠DBE=∠DEB.随堂练习随堂练习2.已知等边△ABC中,DB是AC边上的高,E是BC延长线上一点,且DB=DE,求∠E的度数.提示:证明△CDE是等边三角形即可.3.如图,已知△ABC是等边三角形,P是BC上一点,问在CA和AB上是否存在点Q和R,使△PQR为等边三角形?若存在,求出点Q和R,并加以证明;若不存在.请说明理由.APBC●●Q●R提示:使AR=BP=CQ即可.随堂练习 1.等边三角形的性质.
这节课你有何收获2.等边三角形的判定.3.直角三角形中常用的边角数量关系再 见
等边三角形学习目标
1.理解并掌握等边三角形的定义,探索等边三角形的性质和判定方法,能够用等边三角形的知识解决相应的数学问题。
2.掌握含30o角的直角三角形的性质,并能灵活运用这一性质解决实际问题。
学习重难点
1.重点难点等边三角形性质和判定的应用。
2.含30°角的直角三角形的性质定理的应用。等边对等角三线合一等角对等边两边相等两腰相等轴对称图形知识回顾: 在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等。 我们把三条边都相等的三角形叫做等边三角形(正三角形)。学习概念:等边三角形1、等边三角形的内角什么关系? 为什么?∵ AB=AC=BC
∴ ∠A=∠B=∠C(等边对等角)
∵ ∠A+∠B+∠C=180°
∴ ∠A=∠B=∠C=60°探究一2、等边三角形有“三线合一”的性质吗?
为什么?结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。探究二3、等边三角形是轴对称图形吗?有几条对称轴?探究三对称轴:顶角平分线或底边上的中线、高所在的直线等边三角形的性质2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.4.等边三角形是轴对称图形,有三条对称轴.
1 .三条边相等小 结 :1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.牛刀小试等边603 4、已知△ABC中,∠A=∠B=60°,AB=3cm 则△ABC的周长________5、 △ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______9cm5cm⒈ 三个角都相等的三角形是等边三角形.⒉ 有一个角是60°的等腰三角形是等边三角形.一个三角形满足什么条件就是等边三角形?探究四在等边三角形ABC的边,AB 、AC上分别截取AD=AE, 三角形ADE是什么三角形?说明理由。典例分析一 答:是等边三角形。证明:∵⊿ABC是等边三角形,
∴∠A=∠B=∠C=60°
∵AD=AE
∴⊿ADE是等边三角形。(有一个角是60°的等腰三角形是等边三角形)探究五 将两个含有板有30°的三角尺如图摆放在一起你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?∵△ABC与△ADC关于AC轴对称
∴AB=AD
△ABD是等边三角形
又∵AC⊥BD∴BC=DC=1/2AB探索分析: 解:∵DE⊥AC,BC⊥AC,∠A=30°
∴BC=1/2AB,DE=1/2AD
∴BC=1/2×10=5(m)
又∵AD=1/2AB
∴DE=1/2AD=1/2×5=2.5(m)
答:立柱BC的长上5m,DE的长是2.5m. 下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=10m,∠A=30°,立柱BC,DE要多长?典例分析二1.△ABC是等边三角形,D为AC的中点,延长BC到E,使CE=CD,
求证:BD=DE.提示:证明∠DBE=∠DEB.随堂练习随堂练习2.已知等边△ABC中,DB是AC边上的高,E是BC延长线上一点,且DB=DE,求∠E的度数.提示:证明△CDE是等边三角形即可.3.如图,已知△ABC是等边三角形,P是BC上一点,问在CA和AB上是否存在点Q和R,使△PQR为等边三角形?若存在,求出点Q和R,并加以证明;若不存在.请说明理由.APBC●●Q●R提示:使AR=BP=CQ即可.随堂练习 1.等边三角形的性质.
这节课你有何收获2.等边三角形的判定.3.直角三角形中常用的边角数量关系再 见
