11.1.1 三角形的边课件
文档属性
| 名称 | 11.1.1 三角形的边课件 |  | |
| 格式 | zip | ||
| 文件大小 | 306.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-28 12:37:05 | ||
图片预览



文档简介
课件16张PPT。第十一章 三角形金字塔分子结构香港中银大厦你能从中找到自己熟悉的图形吗? ★ 你所了解的三角形有什么特点? ?★ 你能根据自己的观察,给三角形下一个定义吗?观察思考 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形. 认识新知认识新知 如图所示,
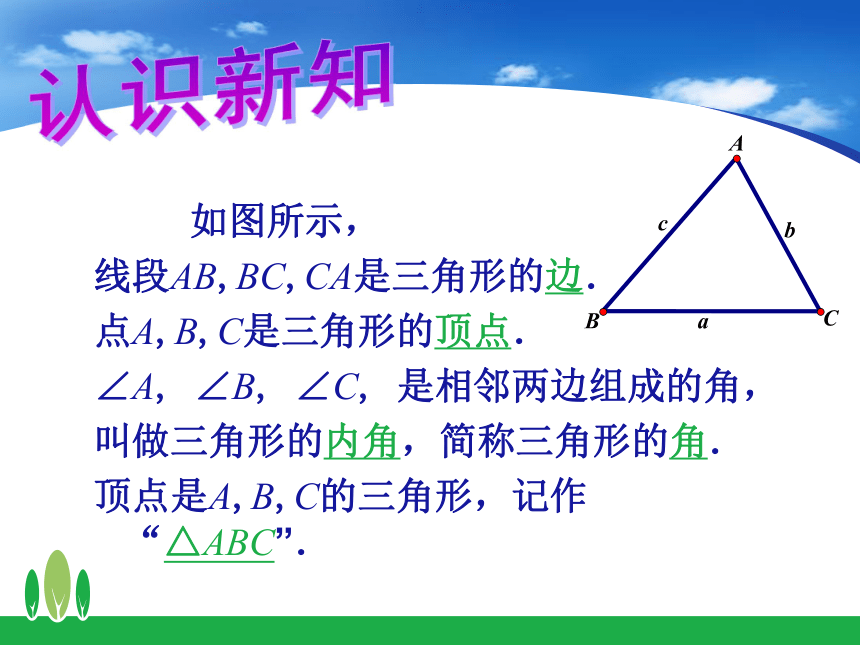
线段AB,BC,CA是三角形的边.
点A,B,C是三角形的顶点.
∠A, ∠B, ∠C, 是相邻两边组成的角,
叫做三角形的内角,简称三角形的角.
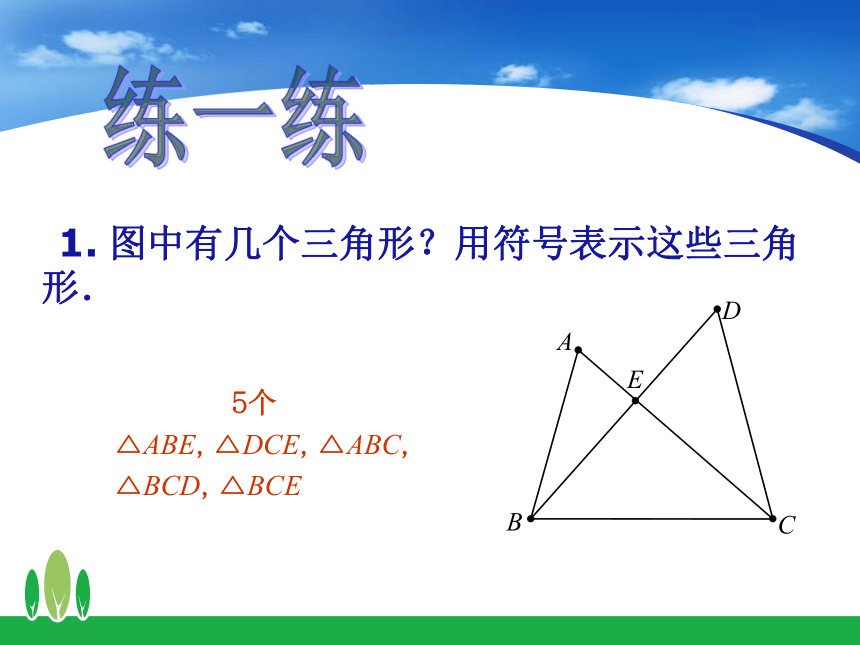
顶点是A,B,C的三角形,记作“△ABC”.cbaCBA 1. 图中有几个三角形?用符号表示这些三角形.
5个
△ABE, △DCE, △ABC,
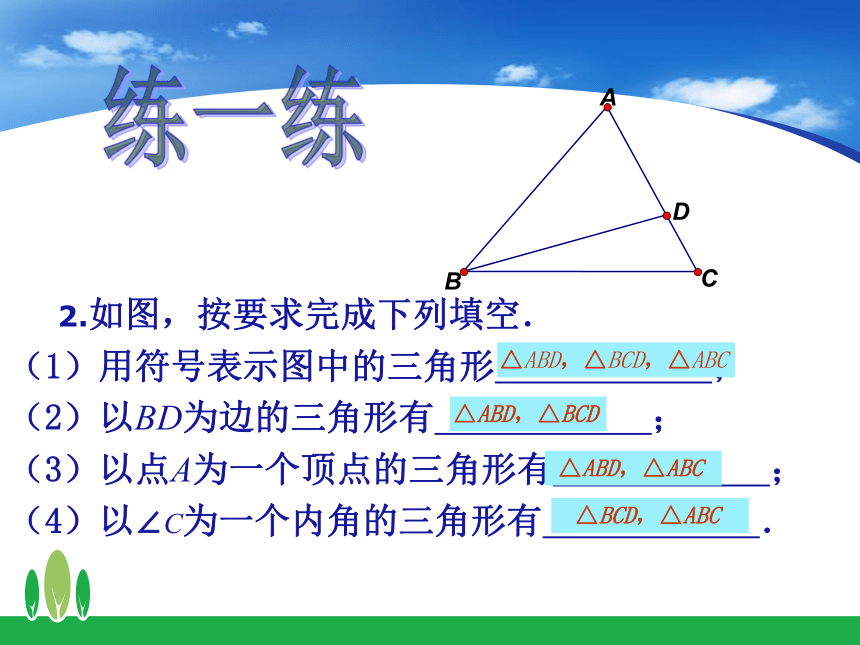
△BCD, △BCE练一练 2.如图,按要求完成下列填空.
(1)用符号表示图中的三角形 ;
(2)以BD为边的三角形有 ;
(3)以点A为一个顶点的三角形有 ;
(4)以∠C为一个内角的三角形有 .练一练△ABD,△BCD,△ABC △ABD,△BCD △ABD,△ABC △BCD,△ABC 探究图上的三角形分别有怎样的特点?它们属于哪一种三角形? 归纳【按三个内角大小分】三角形锐角三角形直角三角形钝角三角形【按边的相等关系分】三角形不等边三角形等腰三角形底边和腰不相等
的等腰三角形等边三角形即 任意画一个△ABC,假设一只小虫从
点B出发,沿三角形的边爬到点C,它有几
条线路可以选择?各条线路的长一样吗?动手实践,探索新知三角形两边的和大于第三边
下列长度的三条线段能否组成三角形?
为什么?
(1)3,4,8;
(2)5,6,11;
(3)5,6,10.巩固新知不能不能能巩固应用,深入理解 【例】用一条长为18 cm的细绳围成
一个等腰三角形.
(1)如果腰长是底边的2倍,那么
各边的长是多少?
(2)能围成有一边的长是4 cm的等
腰三角形吗?为什么?补充练习 已知一个三角形的两边长分别为2 cm和13 cm,
若该三角形的周长为奇数,则第三边长为多少? 答案:12 cm或14 cm 归纳小结对自己说,你有什么收获?
对同学说,你有什么温馨提示?
作业必做题:习题11.1第1、2、6、7题.
选做题:如图,线段AB,CD 相交于点O,
能否确定AB +CD 与AD +BC 的大小关系,请
说明理由.
谢谢同学们!
线段AB,BC,CA是三角形的边.
点A,B,C是三角形的顶点.
∠A, ∠B, ∠C, 是相邻两边组成的角,
叫做三角形的内角,简称三角形的角.
顶点是A,B,C的三角形,记作“△ABC”.cbaCBA 1. 图中有几个三角形?用符号表示这些三角形.
5个
△ABE, △DCE, △ABC,
△BCD, △BCE练一练 2.如图,按要求完成下列填空.
(1)用符号表示图中的三角形 ;
(2)以BD为边的三角形有 ;
(3)以点A为一个顶点的三角形有 ;
(4)以∠C为一个内角的三角形有 .练一练△ABD,△BCD,△ABC △ABD,△BCD △ABD,△ABC △BCD,△ABC 探究图上的三角形分别有怎样的特点?它们属于哪一种三角形? 归纳【按三个内角大小分】三角形锐角三角形直角三角形钝角三角形【按边的相等关系分】三角形不等边三角形等腰三角形底边和腰不相等
的等腰三角形等边三角形即 任意画一个△ABC,假设一只小虫从
点B出发,沿三角形的边爬到点C,它有几
条线路可以选择?各条线路的长一样吗?动手实践,探索新知三角形两边的和大于第三边
下列长度的三条线段能否组成三角形?
为什么?
(1)3,4,8;
(2)5,6,11;
(3)5,6,10.巩固新知不能不能能巩固应用,深入理解 【例】用一条长为18 cm的细绳围成
一个等腰三角形.
(1)如果腰长是底边的2倍,那么
各边的长是多少?
(2)能围成有一边的长是4 cm的等
腰三角形吗?为什么?补充练习 已知一个三角形的两边长分别为2 cm和13 cm,
若该三角形的周长为奇数,则第三边长为多少? 答案:12 cm或14 cm 归纳小结对自己说,你有什么收获?
对同学说,你有什么温馨提示?
作业必做题:习题11.1第1、2、6、7题.
选做题:如图,线段AB,CD 相交于点O,
能否确定AB +CD 与AD +BC 的大小关系,请
说明理由.
谢谢同学们!
