11.1.2-2 三角形的高、中线与角平分线及三角形的稳定性课件
文档属性
| 名称 | 11.1.2-2 三角形的高、中线与角平分线及三角形的稳定性课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 917.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-28 12:40:57 | ||
图片预览




文档简介
课件23张PPT。第十一章 三角形11.1.2 三角形的高、中线与
角平分线11.1.3 三角形的稳定性还记得吗? (1)如何过一点画已知直线的垂线?
(2)如何画线段AB的中点?
(3)如何画∠ACB的平分线? 想一想:
过三角形的一个
顶点,你能画出它
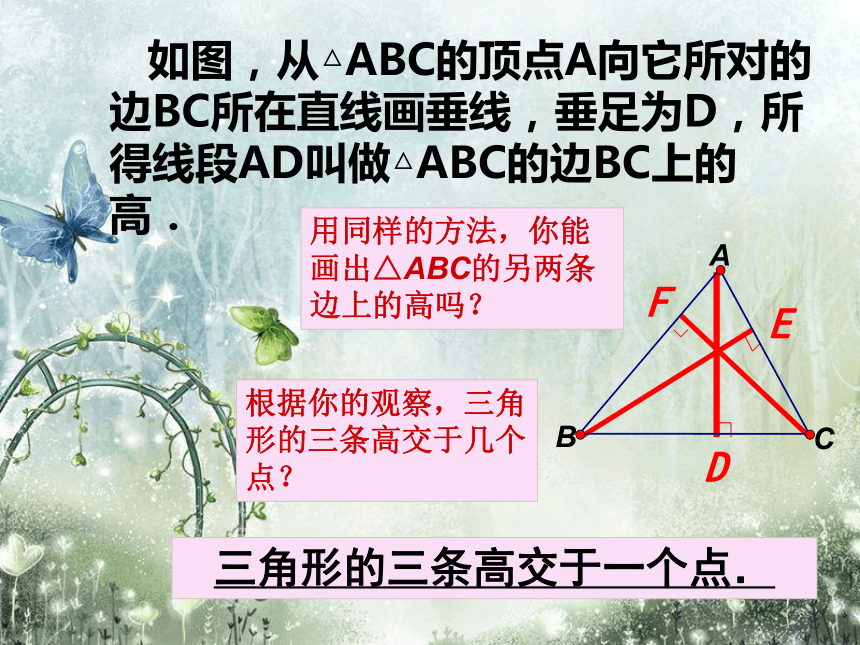
的对边的垂线吗? 如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
用同样的方法,你能画出△ABC的另两条边上的高吗?根据你的观察,三角形的三条高交于几个点?三角形的三条高交于一个点.DEF 【巩固练习】
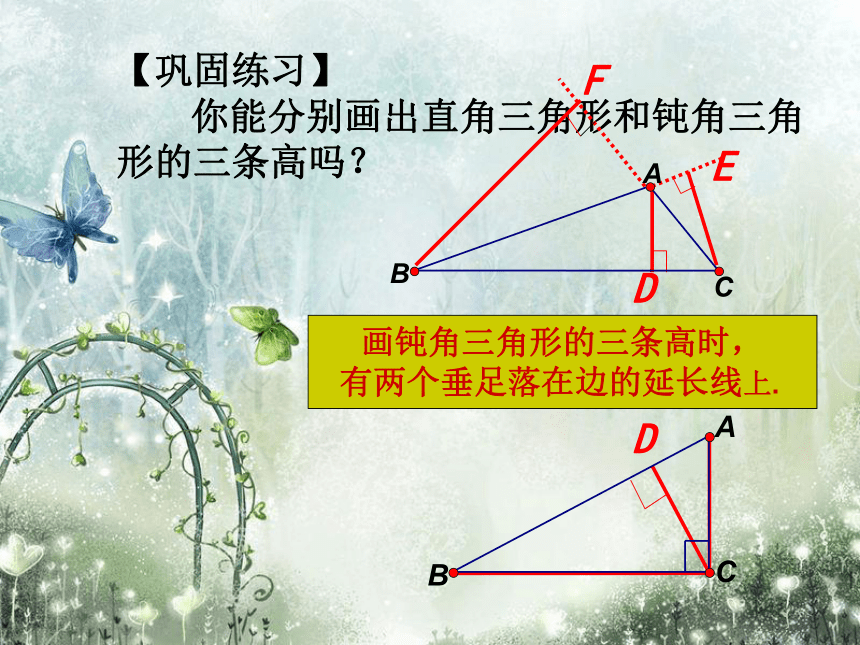
你能分别画出直角三角形和钝角三角形的三条高吗? 画钝角三角形的三条高时,
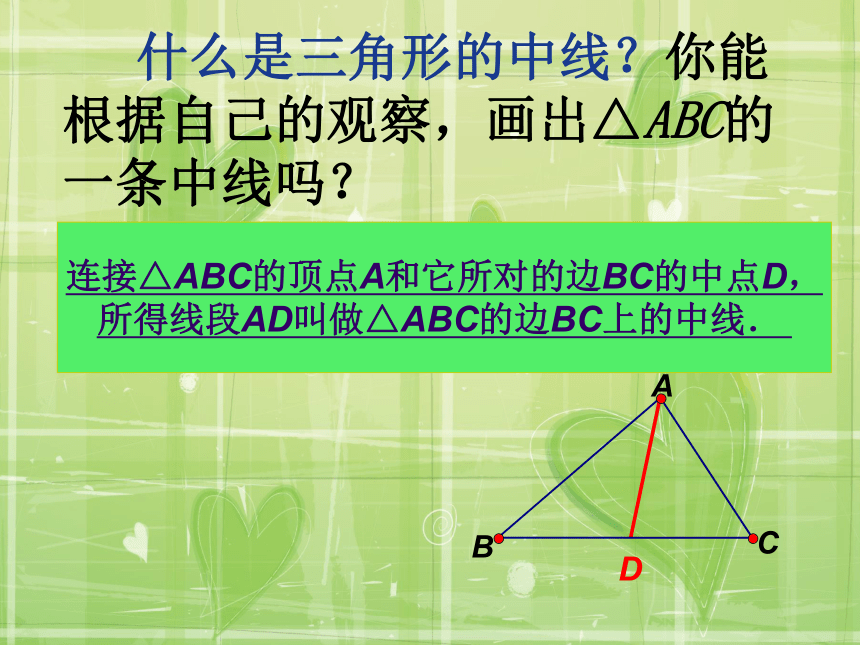
有两个垂足落在边的延长线上. DEFD 什么是三角形的中线?你能根据自己的观察,画出△ABC的一条中线吗?连接△ABC的顶点A和它所对的边BC的中点D,
所得线段AD叫做△ABC的边BC上的中线. D【练习】
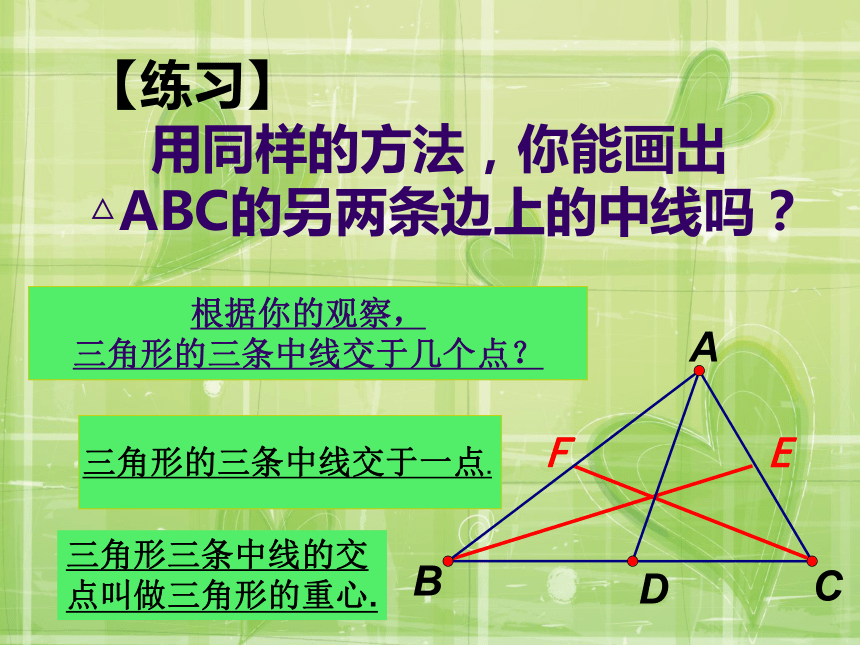
用同样的方法,你能画出△ABC的另两条边上的中线吗?根据你的观察,
三角形的三条中线交于几个点?三角形的三条中线交于一点. EF三角形三条中线的交点叫做三角形的重心.【巩固练习】
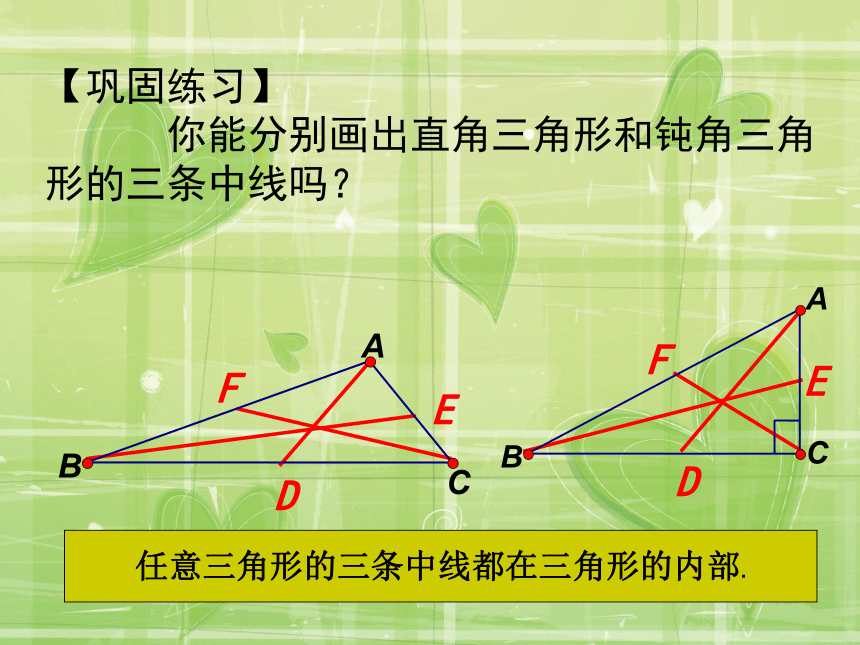
你能分别画出直角三角形和钝角三角形的三条中线吗?任意三角形的三条中线都在三角形的内部.FFDEDE【动手操作】取一块质地均匀的三角形木板,
你能找到它的重心吗? 什么是三角形的角平分线?你能根据自己的观察,画出三角形的一条角平分线吗? D画∠A的平分线AD,交所对的边BC 于点D,所得线段AD 叫做△ABC 的角平分线. 用同样的方法,你能画出△ABC的另两条角平分线吗?根据你的观察,
三角形的三条角平分线交于几个点?三角形的三条角平分线交于一个点.FE【巩固练习】
你能分别画出直角三角形和钝角三角形的三条角平分线吗?
任意三角形的三条角平分线都在三角形的内部 .FDEDEF应用新知,巩固提升如图,(1)(2)和(3)中的三个∠B 有什么不同?
这三条△ABC 的边BC上的高AD 在各自三角形的什么位置?
你能说出其中的规律吗? (1)(2)(3)应用新知,巩固提升(1)如图(1),AD,BE,CF是△ABC的三条
中线,则AB=2 ,BD= ,AE=1/2 .
(2)如图(2),AD,BE,CF是△ABC的三条
角平分线,则∠1= , ∠3 =1/2 ,
∠ACB=2 .(1)(2)AFCDAC∠4∠ABC∠2应用新知,巩固提升【巩固练习】
如图,在△ABC中,AB=2.5 cm,BC= 4 cm,△ABC的高AD与CE的比是多少?
(提示:利用三角形的面积公式)应用新知,巩固提升【巩固练习】
如图,AD是△ABC的角平分线,DE∥AC,
DE交AB于E,DF∥AB,DF交AC于F.
图中∠1与∠2有什么关系?为什么?知识延伸,生活链接 盖房子时,在窗框未安装好之前,木工师傅常常现在窗框上斜钉一根木条.为什么要这样做? 三角形
具有稳定性,
四边形
不具有稳定性.思考:
如图(1),将三根木条用钉子钉成一个三角形
木架,然后扭动它,它的形状会改变吗?
如图(2),将四根木条用钉子钉成一个四边形
木架,然后扭动它,它的形状会改变吗?
如图(3),在四边形木架上再钉一根木条,将
它的一对顶点连接起来,然后再扭动它,这时
木架的形状还会改变吗?为什么?
三角形的稳定性有广泛的应用,
你能再举一些例子吗?练一练:下列图形中哪些具有稳定性?√√√×××想一想: 要使四边形木架(用4根木条钉成)
不变形,至少要再钉上几根木条?
五边形木架和六边形木架呢?归纳总结,布置作业通过学习这节课,你有什么收获? 作业:
复习题11第1题. 同学们再见!
角平分线11.1.3 三角形的稳定性还记得吗? (1)如何过一点画已知直线的垂线?
(2)如何画线段AB的中点?
(3)如何画∠ACB的平分线? 想一想:
过三角形的一个
顶点,你能画出它
的对边的垂线吗? 如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高.
用同样的方法,你能画出△ABC的另两条边上的高吗?根据你的观察,三角形的三条高交于几个点?三角形的三条高交于一个点.DEF 【巩固练习】
你能分别画出直角三角形和钝角三角形的三条高吗? 画钝角三角形的三条高时,
有两个垂足落在边的延长线上. DEFD 什么是三角形的中线?你能根据自己的观察,画出△ABC的一条中线吗?连接△ABC的顶点A和它所对的边BC的中点D,
所得线段AD叫做△ABC的边BC上的中线. D【练习】
用同样的方法,你能画出△ABC的另两条边上的中线吗?根据你的观察,
三角形的三条中线交于几个点?三角形的三条中线交于一点. EF三角形三条中线的交点叫做三角形的重心.【巩固练习】
你能分别画出直角三角形和钝角三角形的三条中线吗?任意三角形的三条中线都在三角形的内部.FFDEDE【动手操作】取一块质地均匀的三角形木板,
你能找到它的重心吗? 什么是三角形的角平分线?你能根据自己的观察,画出三角形的一条角平分线吗? D画∠A的平分线AD,交所对的边BC 于点D,所得线段AD 叫做△ABC 的角平分线. 用同样的方法,你能画出△ABC的另两条角平分线吗?根据你的观察,
三角形的三条角平分线交于几个点?三角形的三条角平分线交于一个点.FE【巩固练习】
你能分别画出直角三角形和钝角三角形的三条角平分线吗?
任意三角形的三条角平分线都在三角形的内部 .FDEDEF应用新知,巩固提升如图,(1)(2)和(3)中的三个∠B 有什么不同?
这三条△ABC 的边BC上的高AD 在各自三角形的什么位置?
你能说出其中的规律吗? (1)(2)(3)应用新知,巩固提升(1)如图(1),AD,BE,CF是△ABC的三条
中线,则AB=2 ,BD= ,AE=1/2 .
(2)如图(2),AD,BE,CF是△ABC的三条
角平分线,则∠1= , ∠3 =1/2 ,
∠ACB=2 .(1)(2)AFCDAC∠4∠ABC∠2应用新知,巩固提升【巩固练习】
如图,在△ABC中,AB=2.5 cm,BC= 4 cm,△ABC的高AD与CE的比是多少?
(提示:利用三角形的面积公式)应用新知,巩固提升【巩固练习】
如图,AD是△ABC的角平分线,DE∥AC,
DE交AB于E,DF∥AB,DF交AC于F.
图中∠1与∠2有什么关系?为什么?知识延伸,生活链接 盖房子时,在窗框未安装好之前,木工师傅常常现在窗框上斜钉一根木条.为什么要这样做? 三角形
具有稳定性,
四边形
不具有稳定性.思考:
如图(1),将三根木条用钉子钉成一个三角形
木架,然后扭动它,它的形状会改变吗?
如图(2),将四根木条用钉子钉成一个四边形
木架,然后扭动它,它的形状会改变吗?
如图(3),在四边形木架上再钉一根木条,将
它的一对顶点连接起来,然后再扭动它,这时
木架的形状还会改变吗?为什么?
三角形的稳定性有广泛的应用,
你能再举一些例子吗?练一练:下列图形中哪些具有稳定性?√√√×××想一想: 要使四边形木架(用4根木条钉成)
不变形,至少要再钉上几根木条?
五边形木架和六边形木架呢?归纳总结,布置作业通过学习这节课,你有什么收获? 作业:
复习题11第1题. 同学们再见!
