12.2 三角形全等的判定( 第1课时 )课件
文档属性
| 名称 | 12.2 三角形全等的判定( 第1课时 )课件 |  | |
| 格式 | zip | ||
| 文件大小 | 141.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-28 14:50:34 | ||
图片预览




文档简介
课件22张PPT。第十二章 全等三角形复习提问 如图,1.能够 的两三角形叫做全等三角形.
2.全等三角形对应边 ,对应角 .完全重合相等相等复习提问 问题: 如图,△ABC≌△A ′ B ′ C ′ ,点A与点A ′ ,点B与点B ′是对应顶点,试找出其中相等的线段和相等的角. 问题:
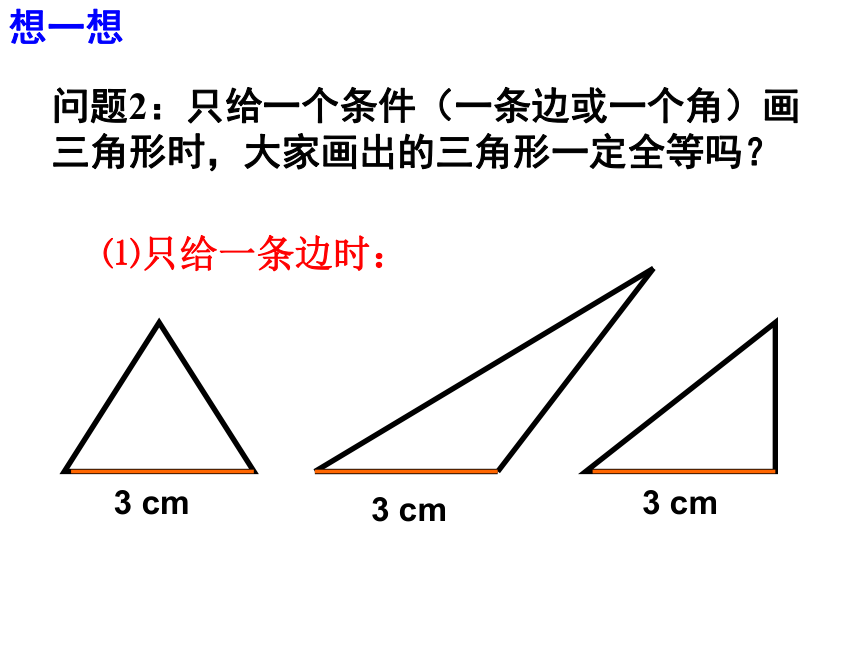
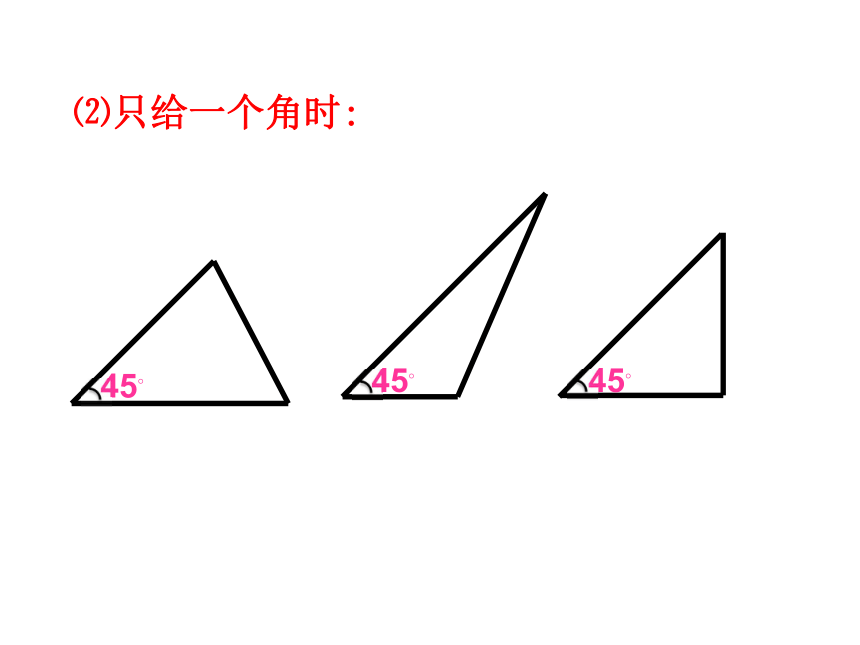
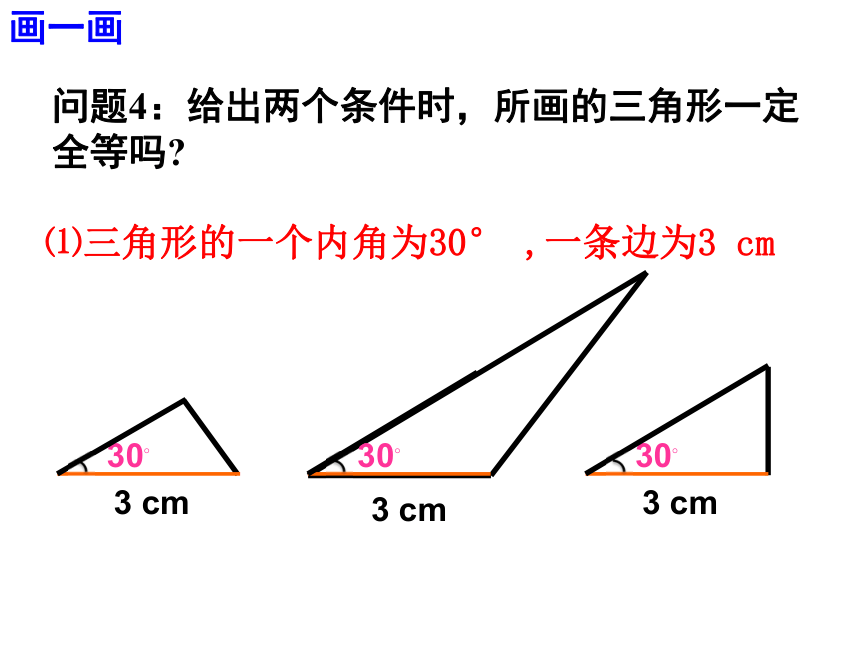
如果两个三角形满足三条边分别相等,三个角分别相等这六个条件,能否判定这两个三角形全等呢?创设情境 两个三角形全等是不是一定要具备这六个条件呢?满足上面六个条件中的一部分是否就能保证两个三角形全等呢?问题1:两个三角形满足上面六个条件中的一个条件,有几种情况?创设情境一条边相等一个角相等 3 cm3 cm3 cm⑴只给一条边时:问题2:只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?想一想⑵只给一个角时:问题3:两个三角形满足上面六个条件中的两个条件,有几种情况?想一想两条边一条边,一个角两个角⑴三角形的一个内角为30° ,一条边为3 cm3 cm3 cm3 cm30?30?30?问题4:给出两个条件时,所画的三角形一定全等吗?画一画⑵如果三角形的两个内角分别是30°,45°时30?30?45?45?⑶如果三角形的两边分别为4 cm,6 cm 时6 cm6 cm6 4 cm4 cm议一议 如果给出三个条件画三角形,你能说出有哪几种可能的情况?1.三个角
2.三条边
3.两边一角
4.两角一边做一做(1)三个内角分别相等的两个三角形全等吗? (2)三条边分别相等的两个三角形全等吗?不一定全等符号语言在△ABC和△DEF中,∴ △ABC≌△DEF (SSS).三边分别相等的两个三角形全等,
简写为“边边边”或“SSS”.定理 由三边分别相等判定三角形全等的结论,还可以得到用直尺和圆规作一个角等于已知角的方法. 简单应用为什么这样作出的两个角是相等的?例1 已知:如图,AB=AD,BC=CD.
求证:(1)△ABC≌ ;
(2)∠B=∠D. △ADC简单应用例2 如图,点A,B在OC上,OM=AN,MB=NC,OA=BC .
求证:(1)△OMB≌△ANC;
(2)∠O=∠NAC.简单应用例3 如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.
求证:(1)∠ADB=∠ADC;
(2)AD⊥BC.综合应用例4 已知:如图,点D,B在AE上,AD=BE,AC=DF,BC=EF.
求证:BC∥EF.综合应用归纳小结1.知识:三角形全等的判定条件——“边边边”条件.
2.方法:会用“边边边”条件证明两个三角形全等,进而证明角相等、线平行、线垂直等.测验
已知:如图,点E,F在AC上,AB=CD,BE=DF,AF=CE.
求证: (1) △ABE ≌ △CDF;
(2) AB∥CD.同学们再见!
2.全等三角形对应边 ,对应角 .完全重合相等相等复习提问 问题: 如图,△ABC≌△A ′ B ′ C ′ ,点A与点A ′ ,点B与点B ′是对应顶点,试找出其中相等的线段和相等的角. 问题:
如果两个三角形满足三条边分别相等,三个角分别相等这六个条件,能否判定这两个三角形全等呢?创设情境 两个三角形全等是不是一定要具备这六个条件呢?满足上面六个条件中的一部分是否就能保证两个三角形全等呢?问题1:两个三角形满足上面六个条件中的一个条件,有几种情况?创设情境一条边相等一个角相等 3 cm3 cm3 cm⑴只给一条边时:问题2:只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?想一想⑵只给一个角时:问题3:两个三角形满足上面六个条件中的两个条件,有几种情况?想一想两条边一条边,一个角两个角⑴三角形的一个内角为30° ,一条边为3 cm3 cm3 cm3 cm30?30?30?问题4:给出两个条件时,所画的三角形一定全等吗?画一画⑵如果三角形的两个内角分别是30°,45°时30?30?45?45?⑶如果三角形的两边分别为4 cm,6 cm 时6 cm6 cm6 4 cm4 cm议一议 如果给出三个条件画三角形,你能说出有哪几种可能的情况?1.三个角
2.三条边
3.两边一角
4.两角一边做一做(1)三个内角分别相等的两个三角形全等吗? (2)三条边分别相等的两个三角形全等吗?不一定全等符号语言在△ABC和△DEF中,∴ △ABC≌△DEF (SSS).三边分别相等的两个三角形全等,
简写为“边边边”或“SSS”.定理 由三边分别相等判定三角形全等的结论,还可以得到用直尺和圆规作一个角等于已知角的方法. 简单应用为什么这样作出的两个角是相等的?例1 已知:如图,AB=AD,BC=CD.
求证:(1)△ABC≌ ;
(2)∠B=∠D. △ADC简单应用例2 如图,点A,B在OC上,OM=AN,MB=NC,OA=BC .
求证:(1)△OMB≌△ANC;
(2)∠O=∠NAC.简单应用例3 如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.
求证:(1)∠ADB=∠ADC;
(2)AD⊥BC.综合应用例4 已知:如图,点D,B在AE上,AD=BE,AC=DF,BC=EF.
求证:BC∥EF.综合应用归纳小结1.知识:三角形全等的判定条件——“边边边”条件.
2.方法:会用“边边边”条件证明两个三角形全等,进而证明角相等、线平行、线垂直等.测验
已知:如图,点E,F在AC上,AB=CD,BE=DF,AF=CE.
求证: (1) △ABE ≌ △CDF;
(2) AB∥CD.同学们再见!
