12.2 三角形全等的判定(第3课时)课件
文档属性
| 名称 | 12.2 三角形全等的判定(第3课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 396.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-28 14:54:07 | ||
图片预览


文档简介
课件16张PPT。第十二章 全等三角形三角形全等的条件三边分别相等
(SSS) 两角一边分别相等两边及其夹角
分别相等 (SAS)?【活动1】复习引入 (1)先在一张纸上任意画出一个△ABC;
(2)然后在另一张纸上画△DEF,
使EF=BC,∠E =∠B, ∠F=∠C.
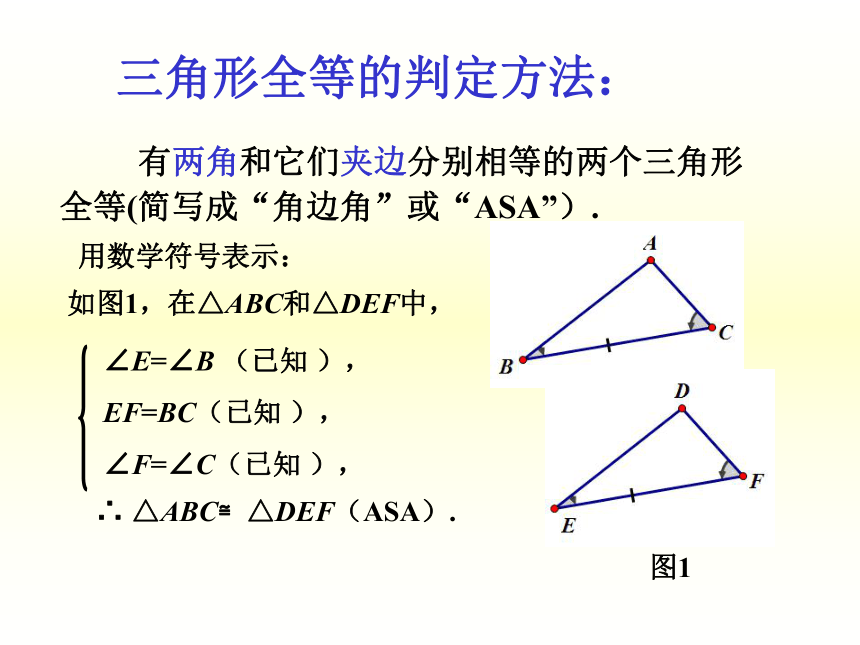
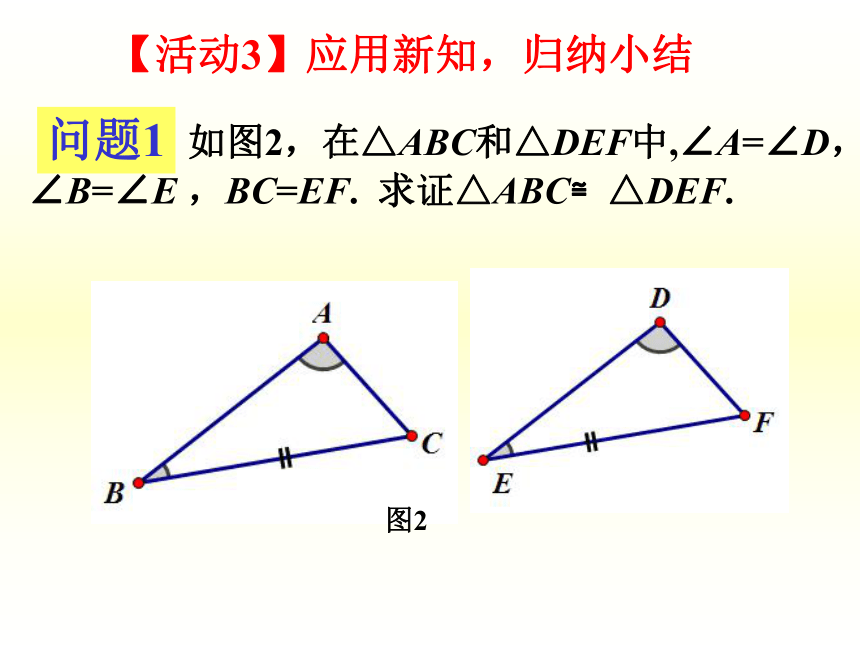
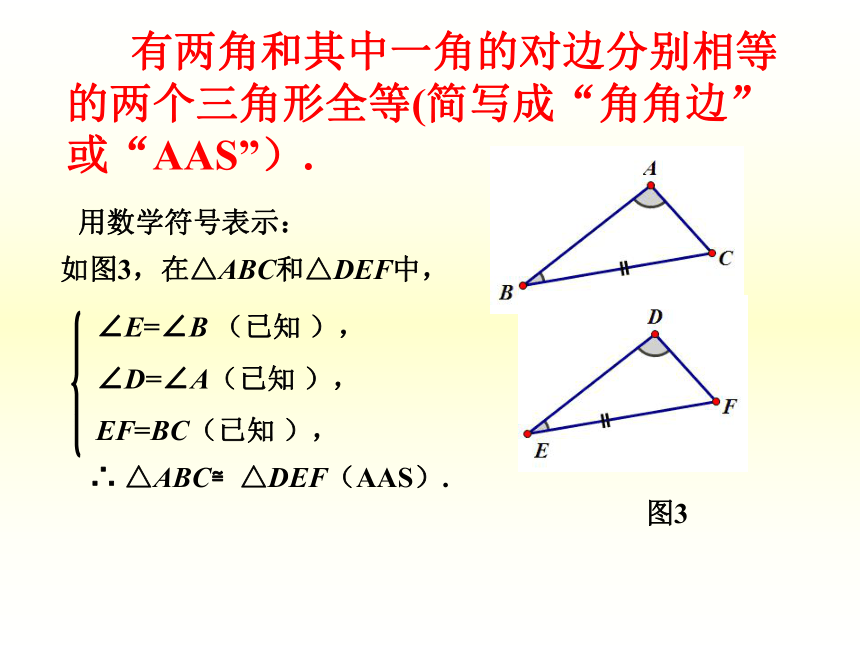
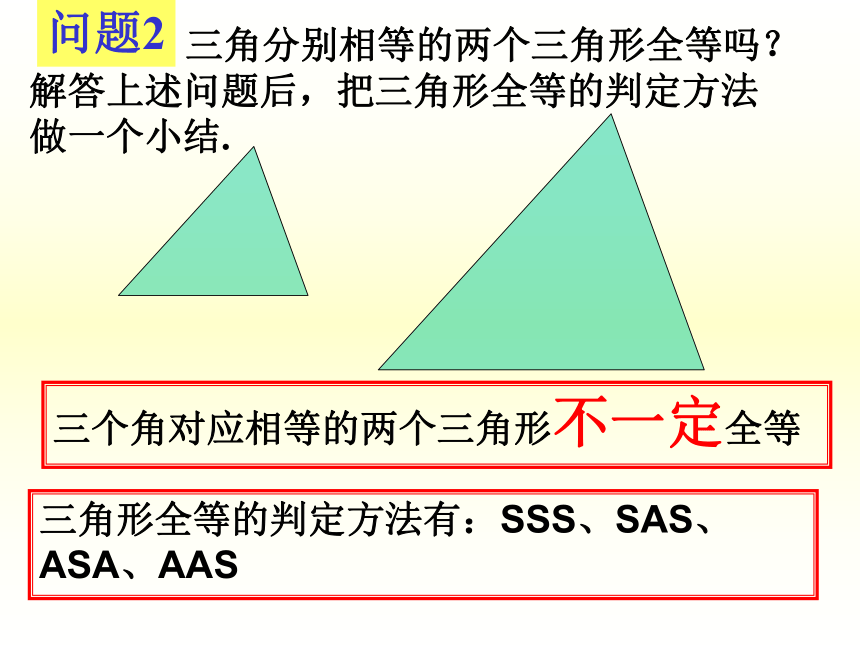
问题1(3)把画好的△DEF 剪下,放到△ABC上,观察它们全等吗?画图观察画法:1. 画EF=BC;2. 在 EF的同旁画∠ME F =∠B , ∠NFE=∠C, EM,FN交于点D. △DEF就是所要画的三角形. 对于任意的两个三角形,当满足“两角及夹边”分别相等时,这两个三角形就一定能够全等吗?问题2gsp1【活动 】动手操作 实践探究2 有两角和它们夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).三角形全等的判定方法:用数学符号表示:图1 如图2,在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF. 求证△ABC≌△DEF.问题1【活动3】应用新知,归纳小结图2 有两角和其中一角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”).用数学符号表示:图3 三角分别相等的两个三角形全等吗?解答上述问题后,把三角形全等的判定方法做一个小结.三个角对应相等的两个三角形不一定全等三角形全等的判定方法有:SSS、SAS、ASA、AAS问题2【活动4】综合应用,拓广探索证明:在△ABE与△ACD中,
∠A=∠A(公共角),
AB=AC(已知),
∠B=∠C(已知),
∴△ABE≌△ACD(ASA),
∴AD=AE(全等三角形的对应边相等).
图4(2)如图5, 若例1中,BE与CD交于点P,
则△DBP≌△ECP吗? 图5图6(3) 在(2)中,再连接AP,如图6,则图中存在几对全等的三角形 ?1.如图7,AB⊥BC, AD⊥DC,垂足分别为B,D,∠1=∠2.
求证AB=AD.练习2.如图8,AB⊥BC, AD⊥DC,∠1=∠2.
“AB=AD”的结论仍然成立吗?若成立,
请给出证明;若不成立,请说明理由. GSP动画演示习题之间的关系图7图8(1)学习了三角形的判定方法:角边角(ASA)、角角边(AAS);
(2)注意角角边、角边角中两角与边的区别;
(3)会根据已知两角画三角形;
(4)进一步学会用推理证明.活动5 归纳小结,反思提高 1. 本节课你有哪些收获?
2.本节课的学习中哪些环节给你留 下的印象最深刻?你还有什么疑问?三角形全等的条件三边分别相等
(SSS) 两角一边分别相等两边及其夹角
分别相等 (SAS)到目前为止我们一共学习了四种三角形全等的判定方法【活动6】布置作业必做题:教材第44页第4、6题.
选做题:教材第56页第9题.
1.如图9,在△ABC与△CDA中,AB∥CD,AD∥BC,求证 AB=CD,AD=BC.2.如图10,已知点A,F在EC上,AB∥DF,BC∥DE,AE=FC,那么AB与DF、BC与DE有怎样的数量关系?请说明理由. 图9 图10【活动7】目标检测GSP展示图形变化 3.李明、张强两位同学在一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了三块,如图所示,两人商量给人家赔偿.你能告诉他们只带其中哪一块去
玻璃店,就可以买到一块完全一样的玻璃吗?怎么办?实际问题谢谢指导
(SSS) 两角一边分别相等两边及其夹角
分别相等 (SAS)?【活动1】复习引入 (1)先在一张纸上任意画出一个△ABC;
(2)然后在另一张纸上画△DEF,
使EF=BC,∠E =∠B, ∠F=∠C.
问题1(3)把画好的△DEF 剪下,放到△ABC上,观察它们全等吗?画图观察画法:1. 画EF=BC;2. 在 EF的同旁画∠ME F =∠B , ∠NFE=∠C, EM,FN交于点D. △DEF就是所要画的三角形. 对于任意的两个三角形,当满足“两角及夹边”分别相等时,这两个三角形就一定能够全等吗?问题2gsp1【活动 】动手操作 实践探究2 有两角和它们夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”).三角形全等的判定方法:用数学符号表示:图1 如图2,在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF. 求证△ABC≌△DEF.问题1【活动3】应用新知,归纳小结图2 有两角和其中一角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”).用数学符号表示:图3 三角分别相等的两个三角形全等吗?解答上述问题后,把三角形全等的判定方法做一个小结.三个角对应相等的两个三角形不一定全等三角形全等的判定方法有:SSS、SAS、ASA、AAS问题2【活动4】综合应用,拓广探索证明:在△ABE与△ACD中,
∠A=∠A(公共角),
AB=AC(已知),
∠B=∠C(已知),
∴△ABE≌△ACD(ASA),
∴AD=AE(全等三角形的对应边相等).
图4(2)如图5, 若例1中,BE与CD交于点P,
则△DBP≌△ECP吗? 图5图6(3) 在(2)中,再连接AP,如图6,则图中存在几对全等的三角形 ?1.如图7,AB⊥BC, AD⊥DC,垂足分别为B,D,∠1=∠2.
求证AB=AD.练习2.如图8,AB⊥BC, AD⊥DC,∠1=∠2.
“AB=AD”的结论仍然成立吗?若成立,
请给出证明;若不成立,请说明理由. GSP动画演示习题之间的关系图7图8(1)学习了三角形的判定方法:角边角(ASA)、角角边(AAS);
(2)注意角角边、角边角中两角与边的区别;
(3)会根据已知两角画三角形;
(4)进一步学会用推理证明.活动5 归纳小结,反思提高 1. 本节课你有哪些收获?
2.本节课的学习中哪些环节给你留 下的印象最深刻?你还有什么疑问?三角形全等的条件三边分别相等
(SSS) 两角一边分别相等两边及其夹角
分别相等 (SAS)到目前为止我们一共学习了四种三角形全等的判定方法【活动6】布置作业必做题:教材第44页第4、6题.
选做题:教材第56页第9题.
1.如图9,在△ABC与△CDA中,AB∥CD,AD∥BC,求证 AB=CD,AD=BC.2.如图10,已知点A,F在EC上,AB∥DF,BC∥DE,AE=FC,那么AB与DF、BC与DE有怎样的数量关系?请说明理由. 图9 图10【活动7】目标检测GSP展示图形变化 3.李明、张强两位同学在一起踢球,不小心把一块三角形的装饰玻璃踢碎了,摔成了三块,如图所示,两人商量给人家赔偿.你能告诉他们只带其中哪一块去
玻璃店,就可以买到一块完全一样的玻璃吗?怎么办?实际问题谢谢指导
