12.2 三角形全等的判定(第5课时)课件
文档属性
| 名称 | 12.2 三角形全等的判定(第5课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 256.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-28 14:56:32 | ||
图片预览




文档简介
课件14张PPT。第十二章 全等三角形思考:
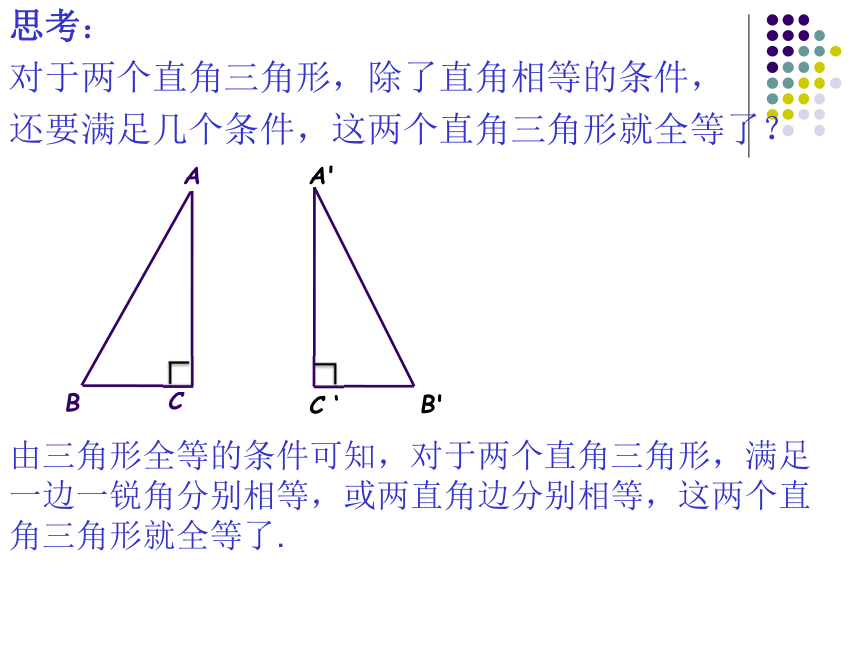
对于两个直角三角形,除了直角相等的条件,
还要满足几个条件,这两个直角三角形就全等了?由三角形全等的条件可知,对于两个直角三角形,满足一边一锐角分别相等,或两直角边分别相等,这两个直角三角形就全等了.探究:
对于两个直角三角形,如果满足斜边和一条直角边分别相等,这两个直角三角形全等吗?∟BAC操作活动:
任意画一个Rt△ABC,使∠C=90°.再画一个
Rt△A′B′C′,使∠C′=90°,C′A′=CA,
A′B′=AB,把画好的Rt△ A′B′C′剪下,
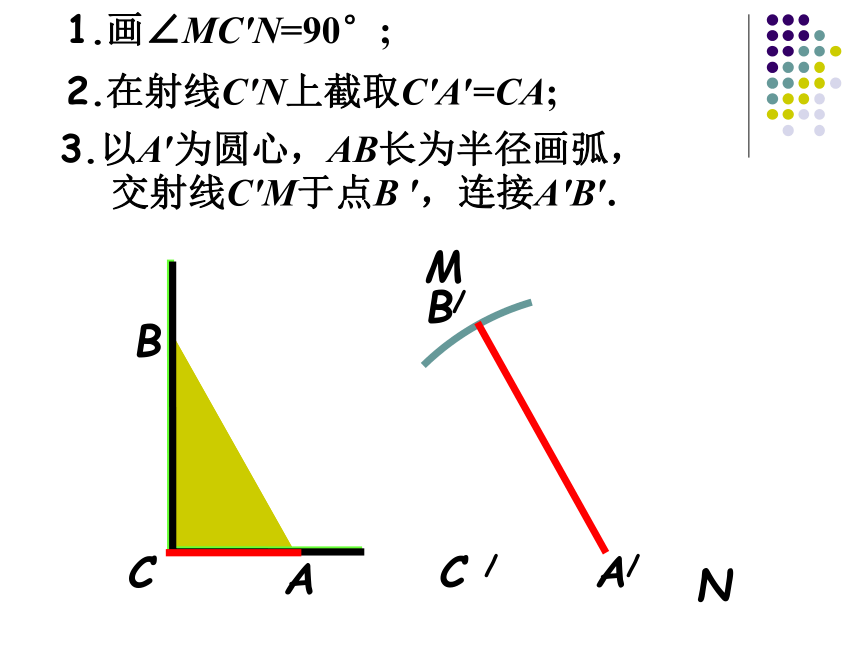
放到Rt△ABC上,它们全等吗?BCAB/C /A/1.画∠MC′N=90°;2.在射线C′N上截取C′A′=CA;3.以A′为圆心,AB长为半径画弧,交射线C′M于点B ′,连接A′B′.MN斜边和一条直角边分别相等的两个直角三角形全等. (简写成“斜边、直角边”或“HL”) 斜边、直角边定理几何语言:在Rt△ABC和 Rt△DEF 中,∵ AB=DE(已知),
AC=DF(已知),
∴Rt△ABC ≌ Rt△DEF(HL).
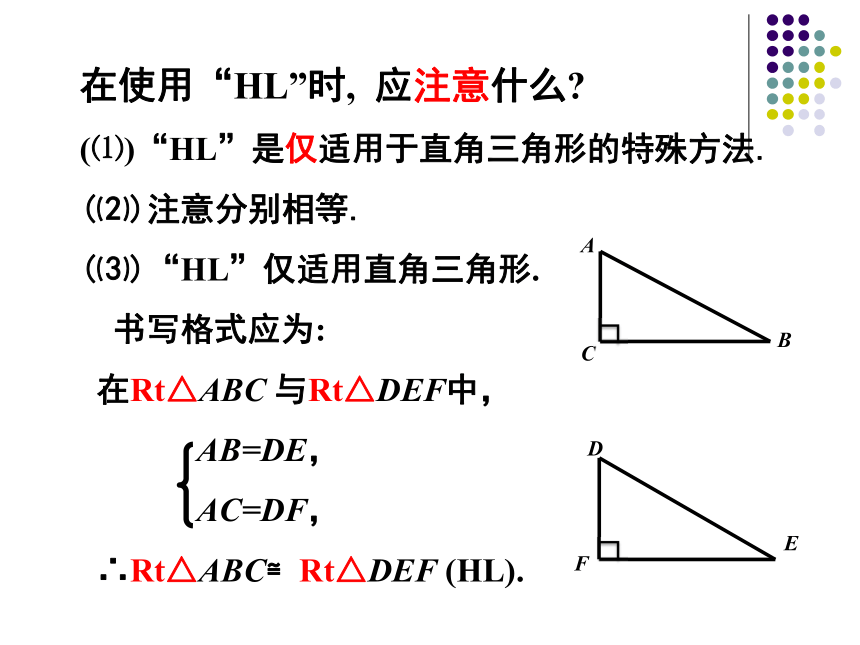
在使用“HL”时, 应注意什么?
“HL”是仅适用于直角三角形的特殊方法.
注意分别相等.
“HL”仅适用直角三角形.
书写格式应为:
在Rt△ABC 与Rt△DEF中,
AB=DE,
AC=DF,
∴Rt△ABC≌Rt△DEF (HL).你能够用几种方法说明两个直角三角形全等? 由于直角三角形是特殊的三角形,所以判定两个直角三角形全等时,不仅可以用一般三角形判定全等的四种方法(SAS 、ASA、 AAS、 SSS),还有直角三角形特有的判定方法“HL”. 要根据问题的实际情况选择方法. 例1.已知:如图,AB⊥BD,CD⊥BD,
AD=BC.
求证:(1)AB=CD; (2)AD∥BC.证明: (1)∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°.
在Rt△ABD和Rt△CDB中,
AD=CB,
BD=DB,
∴Rt△ABD≌Rt△CDB(HL).
∴AB=CD.
(2)∵Rt△ABD≌Rt△CDB,
∴∠ADB=∠CBD,
∴AD∥BC.例2.已知,如图,AC⊥BC,BD⊥AD.
(1)已知∠CAB=∠ DBA,求证:BC=AD.
(2)已知AC=BD,求证:BC=AD.证明:
(1)∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°.
在△ABC和△BAD中,
∠D=∠C,
∠CAB=∠ DBA,
AB=BA,
∴△ABC≌△BAD(AAS).
∴BC=AD.
(2)∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°.
在Rt△ABC和Rt△BAD中,
AB=BA,
AC=BD,
∴Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
例3.已知:如图,AC=BD,AD⊥AC,BC⊥BD.
求证:AD=BC.证明:连接DC.
∵ AD⊥AC,BC⊥BD,
∴∠A=∠B=90°.
在Rt△ADC和Rt△BCD中,
DC=CD,
AC=BD,
∴Rt△ADC≌Rt△BCD(HL).
∴AD=BC.
例4.已知:如图,AE⊥AB,BC⊥AB,
AE=AB,ED=AC.求证:ED⊥AC.证明:∵AE⊥AB,BC⊥AB,
∴∠EAD=∠ABC=90°.
在Rt△EAD和Rt△ABC中,
ED=AC,
EA=AB,
∴ Rt△EAD≌Rt△ABC (HL).
∴∠AED=∠BAC.
∵∠EAF+∠BAC=90°,
∴∠EAF+∠AED=90°,
∴∠EFA=90°,
∴ED⊥AC.
小结 通过本节课的学习你有什么收获?1.如图,△ABC中,AB=AC,AD是高,则_____≌______,
依据是____,由全等得出BD=____,∠BAD=____.
2.如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,
EB=FC,AB=DF,则△ ABC≌_____,全等的根据是_____.
3.如图,已知AB⊥CF,DE ⊥CF,垂足分别为B、E,
AB=DE.请添加一个适当条件,使△ ABC≌ △ DEF,并说明理由
添加条件:___________,理由是:_______________.
课堂检测 第2题图第3题图
对于两个直角三角形,除了直角相等的条件,
还要满足几个条件,这两个直角三角形就全等了?由三角形全等的条件可知,对于两个直角三角形,满足一边一锐角分别相等,或两直角边分别相等,这两个直角三角形就全等了.探究:
对于两个直角三角形,如果满足斜边和一条直角边分别相等,这两个直角三角形全等吗?∟BAC操作活动:
任意画一个Rt△ABC,使∠C=90°.再画一个
Rt△A′B′C′,使∠C′=90°,C′A′=CA,
A′B′=AB,把画好的Rt△ A′B′C′剪下,
放到Rt△ABC上,它们全等吗?BCAB/C /A/1.画∠MC′N=90°;2.在射线C′N上截取C′A′=CA;3.以A′为圆心,AB长为半径画弧,交射线C′M于点B ′,连接A′B′.MN斜边和一条直角边分别相等的两个直角三角形全等. (简写成“斜边、直角边”或“HL”) 斜边、直角边定理几何语言:在Rt△ABC和 Rt△DEF 中,∵ AB=DE(已知),
AC=DF(已知),
∴Rt△ABC ≌ Rt△DEF(HL).
在使用“HL”时, 应注意什么?
“HL”是仅适用于直角三角形的特殊方法.
注意分别相等.
“HL”仅适用直角三角形.
书写格式应为:
在Rt△ABC 与Rt△DEF中,
AB=DE,
AC=DF,
∴Rt△ABC≌Rt△DEF (HL).你能够用几种方法说明两个直角三角形全等? 由于直角三角形是特殊的三角形,所以判定两个直角三角形全等时,不仅可以用一般三角形判定全等的四种方法(SAS 、ASA、 AAS、 SSS),还有直角三角形特有的判定方法“HL”. 要根据问题的实际情况选择方法. 例1.已知:如图,AB⊥BD,CD⊥BD,
AD=BC.
求证:(1)AB=CD; (2)AD∥BC.证明: (1)∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°.
在Rt△ABD和Rt△CDB中,
AD=CB,
BD=DB,
∴Rt△ABD≌Rt△CDB(HL).
∴AB=CD.
(2)∵Rt△ABD≌Rt△CDB,
∴∠ADB=∠CBD,
∴AD∥BC.例2.已知,如图,AC⊥BC,BD⊥AD.
(1)已知∠CAB=∠ DBA,求证:BC=AD.
(2)已知AC=BD,求证:BC=AD.证明:
(1)∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°.
在△ABC和△BAD中,
∠D=∠C,
∠CAB=∠ DBA,
AB=BA,
∴△ABC≌△BAD(AAS).
∴BC=AD.
(2)∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°.
在Rt△ABC和Rt△BAD中,
AB=BA,
AC=BD,
∴Rt△ABC≌Rt△BAD(HL).
∴BC=AD.
例3.已知:如图,AC=BD,AD⊥AC,BC⊥BD.
求证:AD=BC.证明:连接DC.
∵ AD⊥AC,BC⊥BD,
∴∠A=∠B=90°.
在Rt△ADC和Rt△BCD中,
DC=CD,
AC=BD,
∴Rt△ADC≌Rt△BCD(HL).
∴AD=BC.
例4.已知:如图,AE⊥AB,BC⊥AB,
AE=AB,ED=AC.求证:ED⊥AC.证明:∵AE⊥AB,BC⊥AB,
∴∠EAD=∠ABC=90°.
在Rt△EAD和Rt△ABC中,
ED=AC,
EA=AB,
∴ Rt△EAD≌Rt△ABC (HL).
∴∠AED=∠BAC.
∵∠EAF+∠BAC=90°,
∴∠EAF+∠AED=90°,
∴∠EFA=90°,
∴ED⊥AC.
小结 通过本节课的学习你有什么收获?1.如图,△ABC中,AB=AC,AD是高,则_____≌______,
依据是____,由全等得出BD=____,∠BAD=____.
2.如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,
EB=FC,AB=DF,则△ ABC≌_____,全等的根据是_____.
3.如图,已知AB⊥CF,DE ⊥CF,垂足分别为B、E,
AB=DE.请添加一个适当条件,使△ ABC≌ △ DEF,并说明理由
添加条件:___________,理由是:_______________.
课堂检测 第2题图第3题图
