11.3.2 多边形的内角和 优质课件(共33张PPT)
文档属性
| 名称 | 11.3.2 多边形的内角和 优质课件(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 18:10:08 | ||
图片预览





文档简介
(共33张PPT)
11.3.2 多边形的内角和
人教版八年级上册
知识回顾
1. n边形有多少条对角线?
2. 什么是正多边形?
3. 三角形的内角和为多少度?
4. 三角形外角具有什么性质?
教学目标
1.了解并掌握多边形内角和与外角和公式.
2.理解多边形内角和与外角和公式的推导过程.
3.灵活运用多边形的内角和与外角和定理解决实际问题.
新知导入
通过前面的学习我们知道了三角形的内角总为180°,那么多边形的内角和会有什么性质呢?
问题1:正方形内角和为多少度?矩形(长方形)内角和为多少度?
答:矩形和正方形的内角和都是360°.
问题2:矩形和正方形都属于四边形,是不是所有四边形的内角和都是360°呢?
答:矩形和正方形虽然都是四边形,但它们都具有特殊性,并不是每个四边形的内角都是90°,所以我们只能说四边形的内角和可能是360°,这还只是一个猜想。
新知探究
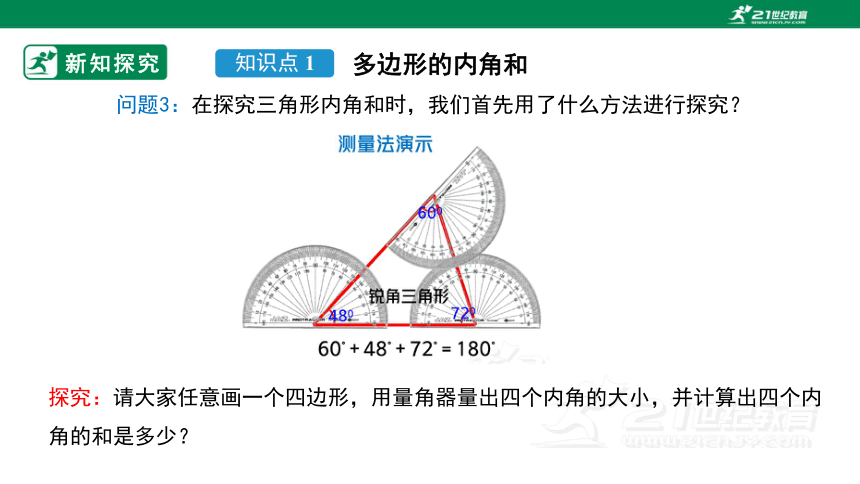
问题3:在探究三角形内角和时,我们首先用了什么方法进行探究?
探究:请大家任意画一个四边形,用量角器量出四个内角的大小,并计算出四个内角的和是多少?
多边形的内角和
知识点 1
新知探究
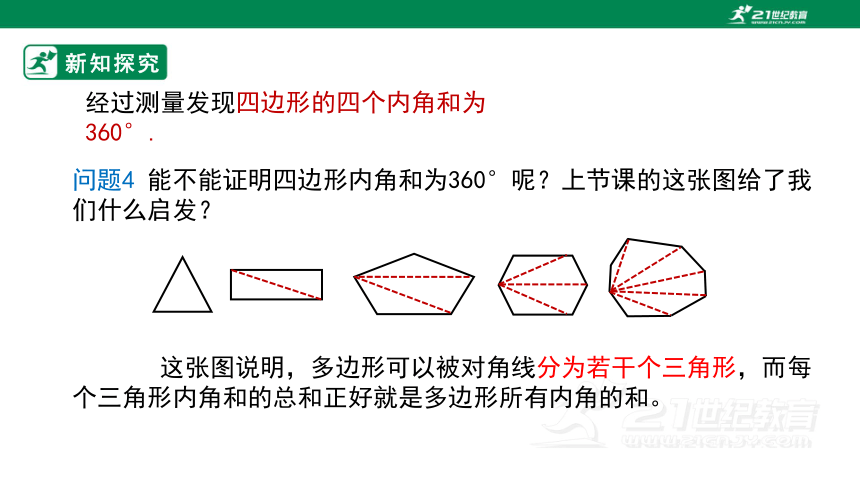
经过测量发现四边形的四个内角和为360°.
问题4 能不能证明四边形内角和为360°呢?上节课的这张图给了我们什么启发?
这张图说明,多边形可以被对角线分为若干个三角形,而每个三角形内角和的总和正好就是多边形所有内角的和。
新知探究
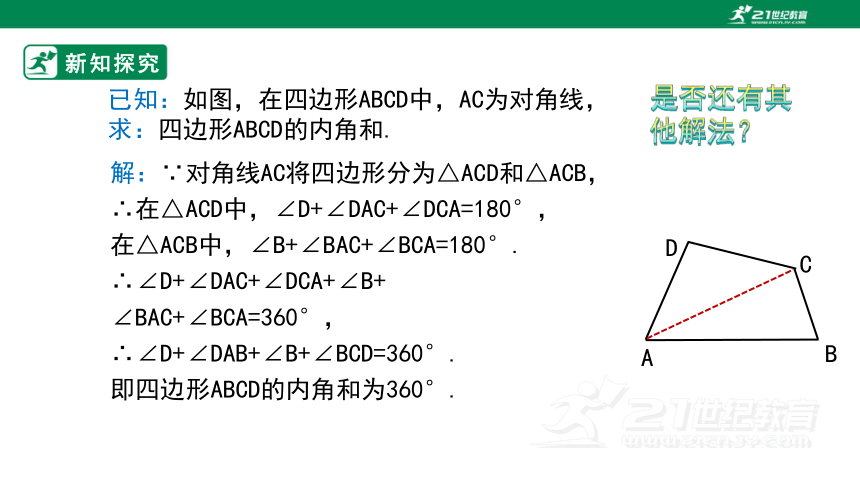
解:∵对角线AC将四边形分为△ACD和△ACB,
∴在△ACD中,∠D+∠DAC+∠DCA=180°,
在△ACB中,∠B+∠BAC+∠BCA=180°.
∴∠D+∠DAC+∠DCA+∠B+
∠BAC+∠BCA=360°,
∴∠D+∠DAB+∠B+∠BCD=360°.
即四边形ABCD的内角和为360°.
已知:如图,在四边形ABCD中,AC为对角线,
求:四边形ABCD的内角和.
A
C
B
D
新知探究
解法二:如图,在AB边上任取一点E,连接CE,DE,
∵在△ADE中,∠A+∠AED+∠ADE=180°
在△CDE中,∠CED+∠ECD+∠CDE=180°
在△BCE中,∠B+∠BCE+∠CEB=180°
∴∠A+∠AED+∠ADE+∠CED+∠ECD+∠CDE+∠B+∠BCE+∠CEB=180°×3=540°
∵∠AED+∠CED+∠CEB=180°
∴∠A+∠B+∠BCD+∠ADC=∠A+∠AED+∠ADE+∠CDE+∠CED+∠ECD+∠BCE+∠B+∠BEC–(∠AED+∠CED+∠BEC)
=180°×3–180°=360° .即四边形ABCD的内角和为360°
E
A
C
B
D
∠ADC
∠BCD
新知探究
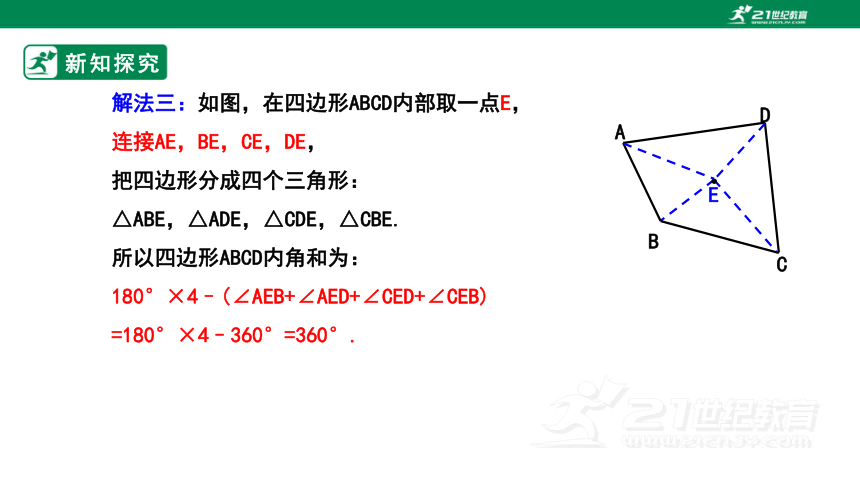
解法三:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:
△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4–(∠AEB+∠AED+∠CED+∠CEB)
=180°×4–360°=360°.
A
B
C
D
E
新知探究
A
B
C
D
P
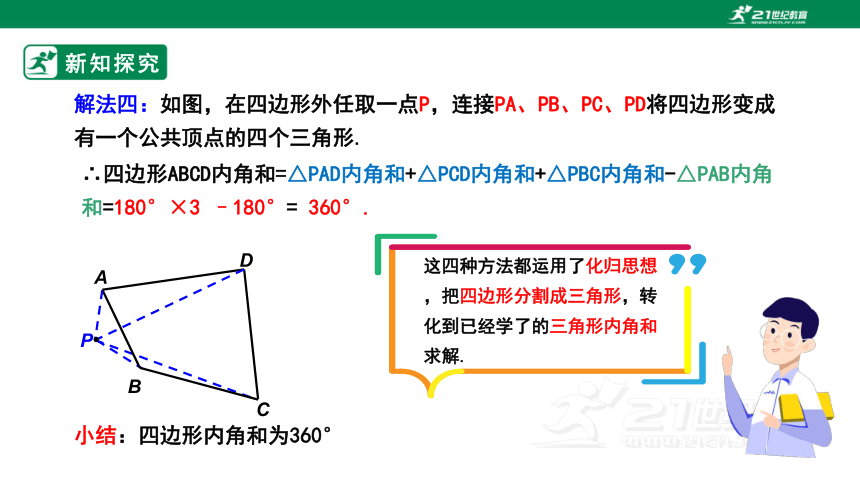
解法四:如图,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形.
∴四边形ABCD内角和=△PAD内角和+△PCD内角和+△PBC内角和-△PAB内角和=180°×3 –180°= 360°.
这四种方法都运用了化归思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.
小结:四边形内角和为360°
新知探究
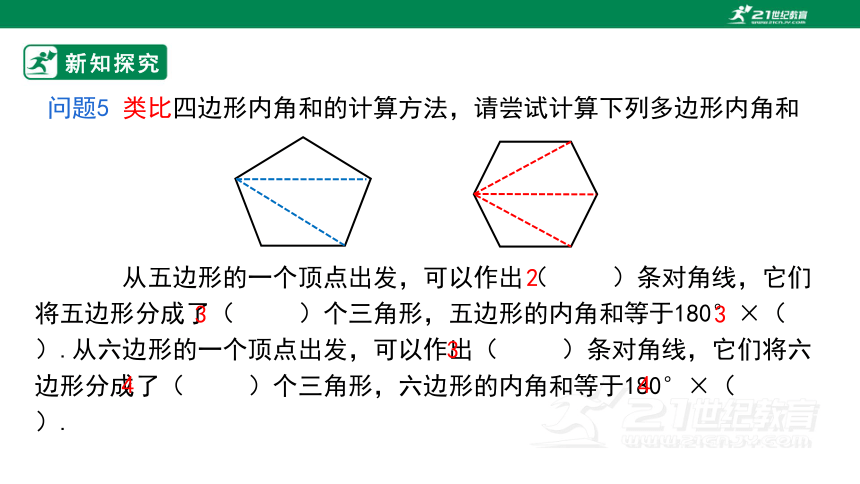
问题5 类比四边形内角和的计算方法,请尝试计算下列多边形内角和
从五边形的一个顶点出发,可以作出( )条对角线,它们将五边形分成了( )个三角形,五边形的内角和等于180°×( ).从六边形的一个顶点出发,可以作出( )条对角线,它们将六边形分成了( )个三角形,六边形的内角和等于180°×( ).
2
3
3
3
4
4
新知探究
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n –3
1
2
3
1
2
3
4
n –2
( n –2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
······
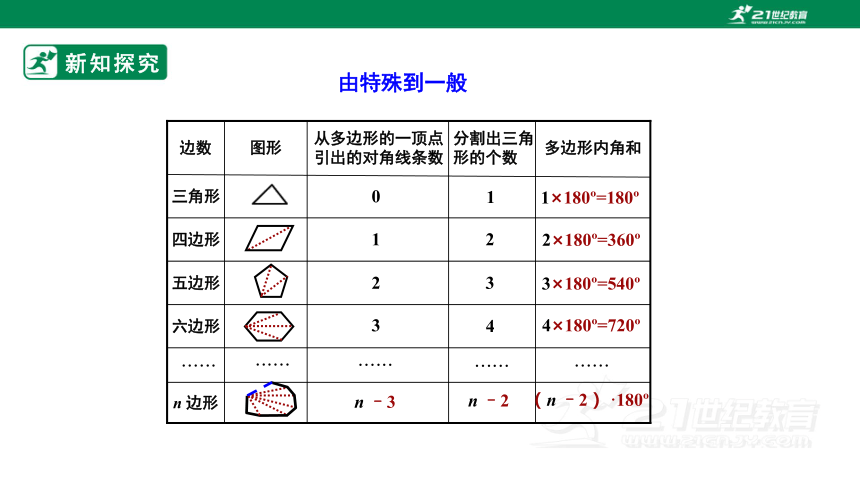
由特殊到一般
新知小结
多边形的内角和公式:
n边形的内角和等于(n-2)×180°.
通过以上的探究,我们发现多边形的内角和与边数之间有密切的关系.从n边形的一个顶点出发,可以作出(n-3)条对角线,它们将n边形分成了(n-2)个三角形,
n边形的内角和等于(n-2)× 180°.
新知典例
例1 求下列图形中x的值.
解:图1:四边形的内角和为:(4﹣2) 180°=360°,
则2x°+150°+80°=360°,
解得x=65;
图2:五边形的内角和为:(5﹣2) 180°=540°,
则3x°+110°+160°+90°=540°,
解得x=60.
新知典例
例2.如图,在四边形ABCD中,∠B+∠D=180°,∠A﹣∠C=20°,求∠B的度数.
解:∵∠B+∠D=180°,
∴∠A+∠C=360°﹣180°=180°,
∵∠A﹣∠C=40°,
∴2∠A=200°,
∴∠A=100°,
∴∠C=80°.
由此题我们可以发现,当四边形中有两角互补时,另外两角也互补
课堂练习
1.如图,∠ABE是四边形ABCD的一个外角,且∠ABE=∠D.那么∠A与∠C互补吗?为什么?
解:∠A与∠C互补.
∵∠ABE=∠D,∠ABE+∠ABC=180°,
∴∠ABC+∠D=180°,
又∵四边形内角和等于360°,
∴∠A+∠C=180°.
新知探究
多边形的外角和
知识点 2
三角形有外角,由三角形组成的多边形当然也有外角,接下来我们就要探究一下多边形的外角。
如图所示,与三角形外角相同,∠ABE就是四边形ABCD的一个外角,显而易见,也与三角形相同,多边形的每一个外角与相邻的内角互补。
问题6 图中四边形有几个外角?(每个顶点只取一个),五边形呢?六边形呢?
答: 四边形有4个外角,五边形有5个外角,六边形有6个外角。
新知探究
也就意味着每个外角的度数是在变化的,外角的个数也是在随着多边形边数在变化,那么外角和是否会像内角和一样,与边数n存在某种数量关系呢?
E
B
C
D
1
2
3
4
5
A
思考:如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.求这个五边形的外角和
求五边形的外角和,也就是求∠1+∠2+∠3+∠4+∠5=?
新知探究
E
B
C
D
1
2
3
4
5
A
已知:五边形ABCDE
求:五边形ABCDE外角和
解:由题可知∠1+∠BAE=180°
∠2+∠ABC=180°
∠3+∠BCD=180°
∠4+∠CDE=180°
∠5+∠AED=180°
∴∠1+∠BAE+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠AED=180°×5
∵五边形内角和为180°×3
∴∠1+∠2+∠3+∠4+∠5=180°×5-180°×3
=180°×2
=360°
n边形的外角和为多少呢?
新知探究
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
–(n–2) × 180°
=360 °
=n个平角–n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考:n边形的外角和又是多少呢?
多边形外角和与边数n无关
多边形外角和等于360°
新知典例
例1 (1)已知一个多边形每一个外角都是40°,则它是 边形
九
解:∵360°÷40°=9,
∴这个多边形的边数是9.
(2)正八边形一个外角的大小为 度.
45
解:∵多边形的外角和等于360°.
∴360°÷8=45°,
故答案为:45.
正多边形每个外角都相等
新知练习
1.若一个多边形的内角和与外角和共1260°,则这个多边形的边数是 .
7
解:多边形的内角和是:1260°﹣360°=900°,
设多边形的边数是n,
则(n﹣2) 180°=900°,
解得:n=7,
2.一个正多边形的每一个内角比每一个外角的3倍还大20°,则这个正多边形的边数为 .
9
解:设每个外角为x°,则内角为(3x+20)°,
∴x+3x+20=180,
解得x=40,
∴边数=360°÷40°=9
课堂归纳
多边形的内角和
内角和计算公式
(n–2) × 180 °(n ≥3的整数)① 边数增加1,内角和增加180°;②内角和是180°的整倍数.
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多
边形
内角= ,外角=
新知练习
1.若n边形的内角和是五边形的外角和的3倍,则n的值为( )
A.6 B.7 C.8 D.9
C
2.五边形ABCDE中,∠A+∠B+∠E=300°,如图,DP、CP分别平分∠EDC、∠BCD,则∠P=( )
A.45° B.60° C.90° D.120°
B
新知练习
3.如果正n边形的一个内角与一个外角的比是3:2,则n= .
4.如图,在五边形ABCDE中,AB∥ED,∠1,∠2,∠3分别是∠ABC,∠BCD,∠CDE的外角,则∠1+∠2+∠3的度数为 .
解:延长BA,DE,
∵AB∥ED,
∴∠4+∠5=180°,
根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°
5
180°
新知练习
5.如图所示,∠1+∠2+∠3+∠4+∠5+∠6= .
360°
解:∵∠7=∠4+∠6,∠8=∠1+∠5,
∠2+∠3+∠7+∠8=360°,
∴∠1+∠2+∠3+∠4+∠5+∠6=360°.
新知练习
6.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数
解:由三角形内角和定理得:∠1+∠5=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=
∠1+∠5+∠2+∠3+∠4+∠6+∠7=
∠8+∠9+∠2+∠3+∠4+∠6+∠7=
180°×(5﹣2)=540°
新知练习
7.如图,沿图中直线将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,求原多边形的边数
解:设多边形截去一个角的边数为n,则
(n﹣2) 180°=1800°,
解得n=12,
∵截去一个角后,边数增加1,
∴原来多边形的边数是12﹣1=11
新知练习
8.如图所示,计算∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△CEG的外角,
∴∠1=∠C+∠E,
同理可得∠AFB=∠B+∠D,
在△AFG中,
∵∠A+∠1+∠AFB=180°,
∴∠A+∠B+∠C+∠D+∠E=180°
新知练习
9.已知一个多边形的内角和再加上一个外角共612° ,则这个多边形的边数是 .
解:设多边形的边数是n,所加的多边形的外角为α,则
(n﹣2) 180°+α=612°,
α=972°﹣180°n,又0<α<180°,
即0<972°﹣180°n<180°,
解得:4.4<n<5.4,又n为正整数,
可得n=5,
此时α=60°满足0<α<180°,
∴这个多边形的边数是5
5
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.3.2 多边形的内角和
人教版八年级上册
知识回顾
1. n边形有多少条对角线?
2. 什么是正多边形?
3. 三角形的内角和为多少度?
4. 三角形外角具有什么性质?
教学目标
1.了解并掌握多边形内角和与外角和公式.
2.理解多边形内角和与外角和公式的推导过程.
3.灵活运用多边形的内角和与外角和定理解决实际问题.
新知导入
通过前面的学习我们知道了三角形的内角总为180°,那么多边形的内角和会有什么性质呢?
问题1:正方形内角和为多少度?矩形(长方形)内角和为多少度?
答:矩形和正方形的内角和都是360°.
问题2:矩形和正方形都属于四边形,是不是所有四边形的内角和都是360°呢?
答:矩形和正方形虽然都是四边形,但它们都具有特殊性,并不是每个四边形的内角都是90°,所以我们只能说四边形的内角和可能是360°,这还只是一个猜想。
新知探究
问题3:在探究三角形内角和时,我们首先用了什么方法进行探究?
探究:请大家任意画一个四边形,用量角器量出四个内角的大小,并计算出四个内角的和是多少?
多边形的内角和
知识点 1
新知探究
经过测量发现四边形的四个内角和为360°.
问题4 能不能证明四边形内角和为360°呢?上节课的这张图给了我们什么启发?
这张图说明,多边形可以被对角线分为若干个三角形,而每个三角形内角和的总和正好就是多边形所有内角的和。
新知探究
解:∵对角线AC将四边形分为△ACD和△ACB,
∴在△ACD中,∠D+∠DAC+∠DCA=180°,
在△ACB中,∠B+∠BAC+∠BCA=180°.
∴∠D+∠DAC+∠DCA+∠B+
∠BAC+∠BCA=360°,
∴∠D+∠DAB+∠B+∠BCD=360°.
即四边形ABCD的内角和为360°.
已知:如图,在四边形ABCD中,AC为对角线,
求:四边形ABCD的内角和.
A
C
B
D
新知探究
解法二:如图,在AB边上任取一点E,连接CE,DE,
∵在△ADE中,∠A+∠AED+∠ADE=180°
在△CDE中,∠CED+∠ECD+∠CDE=180°
在△BCE中,∠B+∠BCE+∠CEB=180°
∴∠A+∠AED+∠ADE+∠CED+∠ECD+∠CDE+∠B+∠BCE+∠CEB=180°×3=540°
∵∠AED+∠CED+∠CEB=180°
∴∠A+∠B+∠BCD+∠ADC=∠A+∠AED+∠ADE+∠CDE+∠CED+∠ECD+∠BCE+∠B+∠BEC–(∠AED+∠CED+∠BEC)
=180°×3–180°=360° .即四边形ABCD的内角和为360°
E
A
C
B
D
∠ADC
∠BCD
新知探究
解法三:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:
△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4–(∠AEB+∠AED+∠CED+∠CEB)
=180°×4–360°=360°.
A
B
C
D
E
新知探究
A
B
C
D
P
解法四:如图,在四边形外任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形.
∴四边形ABCD内角和=△PAD内角和+△PCD内角和+△PBC内角和-△PAB内角和=180°×3 –180°= 360°.
这四种方法都运用了化归思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.
小结:四边形内角和为360°
新知探究
问题5 类比四边形内角和的计算方法,请尝试计算下列多边形内角和
从五边形的一个顶点出发,可以作出( )条对角线,它们将五边形分成了( )个三角形,五边形的内角和等于180°×( ).从六边形的一个顶点出发,可以作出( )条对角线,它们将六边形分成了( )个三角形,六边形的内角和等于180°×( ).
2
3
3
3
4
4
新知探究
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n –3
1
2
3
1
2
3
4
n –2
( n –2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
······
由特殊到一般
新知小结
多边形的内角和公式:
n边形的内角和等于(n-2)×180°.
通过以上的探究,我们发现多边形的内角和与边数之间有密切的关系.从n边形的一个顶点出发,可以作出(n-3)条对角线,它们将n边形分成了(n-2)个三角形,
n边形的内角和等于(n-2)× 180°.
新知典例
例1 求下列图形中x的值.
解:图1:四边形的内角和为:(4﹣2) 180°=360°,
则2x°+150°+80°=360°,
解得x=65;
图2:五边形的内角和为:(5﹣2) 180°=540°,
则3x°+110°+160°+90°=540°,
解得x=60.
新知典例
例2.如图,在四边形ABCD中,∠B+∠D=180°,∠A﹣∠C=20°,求∠B的度数.
解:∵∠B+∠D=180°,
∴∠A+∠C=360°﹣180°=180°,
∵∠A﹣∠C=40°,
∴2∠A=200°,
∴∠A=100°,
∴∠C=80°.
由此题我们可以发现,当四边形中有两角互补时,另外两角也互补
课堂练习
1.如图,∠ABE是四边形ABCD的一个外角,且∠ABE=∠D.那么∠A与∠C互补吗?为什么?
解:∠A与∠C互补.
∵∠ABE=∠D,∠ABE+∠ABC=180°,
∴∠ABC+∠D=180°,
又∵四边形内角和等于360°,
∴∠A+∠C=180°.
新知探究
多边形的外角和
知识点 2
三角形有外角,由三角形组成的多边形当然也有外角,接下来我们就要探究一下多边形的外角。
如图所示,与三角形外角相同,∠ABE就是四边形ABCD的一个外角,显而易见,也与三角形相同,多边形的每一个外角与相邻的内角互补。
问题6 图中四边形有几个外角?(每个顶点只取一个),五边形呢?六边形呢?
答: 四边形有4个外角,五边形有5个外角,六边形有6个外角。
新知探究
也就意味着每个外角的度数是在变化的,外角的个数也是在随着多边形边数在变化,那么外角和是否会像内角和一样,与边数n存在某种数量关系呢?
E
B
C
D
1
2
3
4
5
A
思考:如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.求这个五边形的外角和
求五边形的外角和,也就是求∠1+∠2+∠3+∠4+∠5=?
新知探究
E
B
C
D
1
2
3
4
5
A
已知:五边形ABCDE
求:五边形ABCDE外角和
解:由题可知∠1+∠BAE=180°
∠2+∠ABC=180°
∠3+∠BCD=180°
∠4+∠CDE=180°
∠5+∠AED=180°
∴∠1+∠BAE+∠2+∠ABC+∠3+∠BCD+∠4+∠CDE+∠5+∠AED=180°×5
∵五边形内角和为180°×3
∴∠1+∠2+∠3+∠4+∠5=180°×5-180°×3
=180°×2
=360°
n边形的外角和为多少呢?
新知探究
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
–(n–2) × 180°
=360 °
=n个平角–n边形内角和
= n×180 °
An
A2
A3
A4
1
2
3
4
n
A1
思考:n边形的外角和又是多少呢?
多边形外角和与边数n无关
多边形外角和等于360°
新知典例
例1 (1)已知一个多边形每一个外角都是40°,则它是 边形
九
解:∵360°÷40°=9,
∴这个多边形的边数是9.
(2)正八边形一个外角的大小为 度.
45
解:∵多边形的外角和等于360°.
∴360°÷8=45°,
故答案为:45.
正多边形每个外角都相等
新知练习
1.若一个多边形的内角和与外角和共1260°,则这个多边形的边数是 .
7
解:多边形的内角和是:1260°﹣360°=900°,
设多边形的边数是n,
则(n﹣2) 180°=900°,
解得:n=7,
2.一个正多边形的每一个内角比每一个外角的3倍还大20°,则这个正多边形的边数为 .
9
解:设每个外角为x°,则内角为(3x+20)°,
∴x+3x+20=180,
解得x=40,
∴边数=360°÷40°=9
课堂归纳
多边形的内角和
内角和计算公式
(n–2) × 180 °(n ≥3的整数)① 边数增加1,内角和增加180°;②内角和是180°的整倍数.
外角和
多边形的外角和等于360°
特别注意:与边数无关.
正多
边形
内角= ,外角=
新知练习
1.若n边形的内角和是五边形的外角和的3倍,则n的值为( )
A.6 B.7 C.8 D.9
C
2.五边形ABCDE中,∠A+∠B+∠E=300°,如图,DP、CP分别平分∠EDC、∠BCD,则∠P=( )
A.45° B.60° C.90° D.120°
B
新知练习
3.如果正n边形的一个内角与一个外角的比是3:2,则n= .
4.如图,在五边形ABCDE中,AB∥ED,∠1,∠2,∠3分别是∠ABC,∠BCD,∠CDE的外角,则∠1+∠2+∠3的度数为 .
解:延长BA,DE,
∵AB∥ED,
∴∠4+∠5=180°,
根据多边形的外角和定理可得∠1+∠2+∠3+∠4+∠5=360°,
∴∠1+∠2+∠3=360°﹣180°=180°
5
180°
新知练习
5.如图所示,∠1+∠2+∠3+∠4+∠5+∠6= .
360°
解:∵∠7=∠4+∠6,∠8=∠1+∠5,
∠2+∠3+∠7+∠8=360°,
∴∠1+∠2+∠3+∠4+∠5+∠6=360°.
新知练习
6.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数
解:由三角形内角和定理得:∠1+∠5=∠8+∠9,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=
∠1+∠5+∠2+∠3+∠4+∠6+∠7=
∠8+∠9+∠2+∠3+∠4+∠6+∠7=
180°×(5﹣2)=540°
新知练习
7.如图,沿图中直线将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,求原多边形的边数
解:设多边形截去一个角的边数为n,则
(n﹣2) 180°=1800°,
解得n=12,
∵截去一个角后,边数增加1,
∴原来多边形的边数是12﹣1=11
新知练习
8.如图所示,计算∠A+∠B+∠C+∠D+∠E的度数.
解:∵∠1是△CEG的外角,
∴∠1=∠C+∠E,
同理可得∠AFB=∠B+∠D,
在△AFG中,
∵∠A+∠1+∠AFB=180°,
∴∠A+∠B+∠C+∠D+∠E=180°
新知练习
9.已知一个多边形的内角和再加上一个外角共612° ,则这个多边形的边数是 .
解:设多边形的边数是n,所加的多边形的外角为α,则
(n﹣2) 180°+α=612°,
α=972°﹣180°n,又0<α<180°,
即0<972°﹣180°n<180°,
解得:4.4<n<5.4,又n为正整数,
可得n=5,
此时α=60°满足0<α<180°,
∴这个多边形的边数是5
5
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
